图-Dijkster最短路径

1.题目：过年回家

题目描述：

牛牛今年买了一辆新车，他决定自己开车回家过年。回家过程中要经过n个大小收费站，每个收费站的费用不同，你能帮他计算一下最少需要给多少过路费吗？

   输入描述：

输入包含多组数据，每组数据第一行包含两个正整数m（1≤m≤500）和n（1≤n≤30），其中n表示有n个收费站，编号依次为1、2、…、n。出发地的编号为0，终点的编号为n，即需要从0到n。

紧接着m行，每行包含三个整数f、t、c，（0≤f, t≤n; 1≤c≤10），分别表示从编号为f的地方开到t，需要交c元的过路费。
输出描述：

对应每组数据，请输出至少需要交多少过路费。

示例1

输入：

8 4
0 1 10
0 2 5
1 2 2
1 3 1
2 1 3
2 3 9
2 4 2
3 4 4

输出：

   7

思路：本身考察图的题，图的题之前做的比较少，再来找几道复习下，这道题就是要理解基于贪心的Dijkster算法，这个算法本身还是比较好理解的，看到了一篇介绍的比较详细的博客： 最短路径问题---Dijkstra算法详解

算法的思路

Dijkstra算法采用的是一种贪心的策略，声明一个数组dist来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合：T，初始时，原点 s 的路径权重被赋为 0 （dist[s] = 0）。若对于顶点 s 存在能直接到达的边（s,m），则把dist[m]设为w（s, m）,同时把所有其他（s不能直接到达的）顶点的路径长度设为无穷大。初始时，集合T只有顶点s。 
然后，从dist数组选择最小值，则该值就是源点s到该值对应的顶点的最短路径，并且把该点加入到T中，OK，此时完成一个顶点， 
然后，我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短，如果是，那么就替换这些顶点在dist中的值。 
然后，又从dist中找出最小值，重复上述动作，直到T中包含了图的所有顶点。

算法的演示：

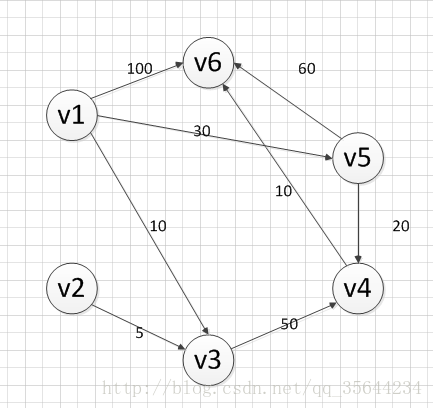
下面我求下图，从顶点v1到其他各个顶点的最短路径

首先第一步，我们先声明一个dis数组，该数组初始化的值为： 

我们的顶点集T的初始化为：T={v1}

既然是求 v1顶点到其余各个顶点的最短路程，那就先找一个离 1 号顶点最近的顶点。通过数组 dis 可知当前离v1顶点最近是 v3顶点。当选择了 2 号顶点后，dis[2]（下标从0开始）的值就已经从“估计值”变为了“确定值”，即 v1顶点到 v3顶点的最短路程就是当前 dis[2]值。将V3加入到T中。 
为什么呢？因为目前离 v1顶点最近的是 v3顶点，并且这个图所有的边都是正数，那么肯定不可能通过第三个顶点中转，使得 v1顶点到 v3顶点的路程进一步缩短了。因为 v1顶点到其它顶点的路程肯定没有 v1到 v3顶点短.

OK，既然确定了一个顶点的最短路径，下面我们就要根据这个新入的顶点V3会有出度，发现以v3 为弧尾的有： < v3,v4 >,那么我们看看路径：v1–v3–v4的长度是否比v1–v4短，其实这个已经是很明显的了，因为dis[3]代表的就是v1–v4的长度为无穷大，而v1–v3–v4的长度为：10+50=60，所以更新dis[3]的值,得到如下结果： 

因此 dis[3]要更新为 60。这个过程有个专业术语叫做“松弛”。即 v1顶点到 v4顶点的路程即 dis[3]，通过 < v3,v4> 这条边松弛成功。这便是 Dijkstra 算法的主要思想：通过“边”来松弛v1顶点到其余各个顶点的路程。

然后，我们又从除dis[2]和dis[0]外的其他值中寻找最小值，发现dis[4]的值最小，通过之前是解释的原理，可以知道v1到v5的最短距离就是dis[4]的值，然后，我们把v5加入到集合T中，然后，考虑v5的出度是否会影响我们的数组dis的值，v5有两条出度：< v5,v4>和 < v5,v6>,然后我们发现：v1–v5–v4的长度为：50，而dis[3]的值为60，所以我们要更新dis[3]的值.另外，v1-v5-v6的长度为：90，而dis[5]为100，所以我们需要更新dis[5]的值。更新后的dis数组如下图： 

然后，继续从dis中选择未确定的顶点的值中选择一个最小的值，发现dis[3]的值是最小的，所以把v4加入到集合T中，此时集合T={v1,v3,v5,v4},然后，考虑v4的出度是否会影响我们的数组dis的值，v4有一条出度：< v4,v6>,然后我们发现：v1–v5–v4–v6的长度为：60，而dis[5]的值为90，所以我们要更新dis[5]的值，更新后的dis数组如下图： 

然后，我们使用同样原理，分别确定了v6和v2的最短路径，最后dis的数组的值如下： 

 

代码：

import java.util.Scanner;
public class Main{
    public static void main(String[]args){
        Scanner in=new Scanner(System.in);
        while(in.hasNext()){
            int m=in.nextInt();
            int n=in.nextInt();
            int[][] Edge=new int[n+1][n+1];//通过临接矩阵来保存图
            int[] dist=new int[n+1];//dist用来保存从起点到每个点的最短路径，到不了的点距离设置为无穷大
            int[]path=new int[n+1];//path用来保存每个点的前一个顶点号，如path[3]=2,则有顶点2->3
            boolean[] s=new boolean[n+1];//s用来记录该点是否已经确定了，初始化都为false,当把该点计入最短路径后，设为true;
            for(int i=0;i<n+1;i++){    //初始化临街矩阵
                for(int j=0;j<n+1;j++){
                    Edge[i][j]=Integer.MAX_VALUE;
                }
            }
            for(int i=0;i<m;i++){       //输入临接矩阵
                Edge[in.nextInt()][in.nextInt()]=in.nextInt();
            }
            Dijkster(Edge,dist,path,s,m,n);
        }
    }
    private static void Dijkster(int[][]Edge,int[]dist,int[]path,boolean[]s,int m,int n){
        for(int i=0;i<n+1;i++){//初始化dist,path
            dist[i]=Edge[0][i];
            if(i!=0&&dist[i]<Integer.MAX_VALUE){
                path[i]=0;
            }else{
                path[i]=-1;
            }
        }
        s[0]=true;//从第一个顶点开始计算
        dist[0]=0;
        for(int i=0;i<n;i++){
            int min=Integer.MAX_VALUE;
            int u=0;
            //选择当前未确定顶点中具有最短路径（离起点最近）的顶点u
            for(int j=0;j<n+1;j++){
                if(!s[j]&&dist[j]<min){
                    u=j;
                    min=dist[j];
                }              
            }
            //此时u已经在最短路径上了，更新s
            s[u]=true;
            for(int k=0;k<n+1;k++){
                if(!s[k]&&Edge[u][k]<Integer.MAX_VALUE&&dist[u]+Edge[u][k]<dist[k]){
                    dist[k]=dist[u]+Edge[u][k];
                    path[k]=u;
                }
            }
        }
         System.out.println(dist[n]);       
    }
}

一般而言，最短路径的题就是这样的解法，学习一下排名第一的解法，算法方面都差不多，但是他使用了java IO流，使得整个程序的执行时间比第二名快了3倍，看来数据量大的时候，Scanner扫描器就不是那么合适了。

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
 
public class Main {
     
    public static void main(String[] args) throws IOException {
        StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
         
        while(in.nextToken() != StreamTokenizer.TT_EOF){
            int m = (int) in.nval;
            in.nextToken();
            int n = (int) in.nval;
            int [][] a = new int [n + 1][n + 1]; // 收费站数目加上起点
            for(int i = 0; i <= n; i++){
                for(int j = 0; j <= n; j++){
                    a[i][j] = Integer.MAX_VALUE;
                }
            }
 
            for(int k = 1; k <= m; k++){ //  用二维数组存储两地通过需要教的路费
                in.nextToken(); int i = (int)in.nval;
                in.nextToken(); int j = (int)in.nval;
                in.nextToken(); a[i][j] = (int)in.nval;
            }
            int s = dijk(a);
            out.println(s);
            out.flush();
        }
         
    }
     
    private static int dijk(int [][] graph){
         
        boolean [] sign = new boolean[graph.length];
        int [] dist = new int [graph.length];
         
        // 遍历第 起始位置能到达的下一个位置， 收费为当前收费站的收费
        for(int i = 0; i< graph.length; i++){
            dist[i] = graph[0][i];
        }
        sign[0] = true;
        // 遍历其他位置、
        for(int i = 1; i < graph.length; i++){
            int min = Integer.MAX_VALUE;
            int u = 0;
            for(int j = 1; j < graph.length; j++){
                if(!sign[j] && dist[j] < min){
                    min = dist[j];
                    u = j;
                }
            }
             
            sign[u] = true;
            for(int j = 1; j < graph.length; j++){
                if(!sign[j] && graph[u][j] < Integer.MAX_VALUE){ // 没被访问过、同时有路可以走、
                    int v = dist[u] + graph[u][j];
                    if(v < dist[j]){
                        dist[j] = v;
                    }
                }
            }
        }
         
        return dist[graph.length - 1];
    }
}

，再来看一题

2.题目：牛牛取快递

题目描述：牛牛的快递到了，他迫不及待地想去取快递，但是天气太热了，以至于牛牛不想在烈日下多走一步。他找来了你，请你帮他规划一下，他最少要走多少距离才能取回快递。 

输入描述:

每个输入包含一个测试用例。
输入的第一行包括四个正整数，表示位置个数N(2<=N<=10000)，道路条数M(1<=M<=100000)，起点位置编号S(1<=S<=N)和快递位置编号T(1<=T<=N)。位置编号从1到N，道路是单向的。数据保证S≠T，保证至少存在一个方案可以从起点位置出发到达快递位置再返回起点位置。
接下来M行，每行包含三个正整数，表示当前道路的起始位置的编号U(1<=U<=N)，当前道路通往的位置的编号V(1<=V<=N)和当前道路的距离D(1<=D<=1000)。

输出描述:

对于每个用例，在单独的一行中输出从起点出发抵达快递位置再返回起点的最短距离。

 

输入例子1:

3 3 1 3 
1 2 3 
2 3 3 
3 1 1

 

输出例子：

7

可以看出，这个题也是在考察最短路径，
如果将上一个题的答案稍加改进，得到

import java.util.Scanner;
public class Dijkster{
    public static void main(String[]args){
        Scanner in=new Scanner(System.in);
        while(in.hasNext()){
            int n=in.nextInt();
            int m=in.nextInt();
            int a=in.nextInt();
            int b=in.nextInt();
            int[][] Edge=new int[n+1][n+1];//通过临接矩阵来保存图


            for(int i=0;i<n+1;i++){    //初始化临街矩阵
                for(int j=0;j<n+1;j++){
                    Edge[i][j]=Integer.MAX_VALUE;
                }
            }
            for(int i=0;i<m;i++){       //输入临接矩阵
               int x=in.nextInt();
                int y=in.nextInt();
                int z=in.nextInt();
                if(Edge[x][y]<Integer.MAX_VALUE){
                    if(z<Edge[x][y])
                        Edge[x][y]=z;
                }

               else
                   Edge[x][y]=z;
            }
           int p= Dijkster(Edge,n,a,b);
            int q= Dijkster(Edge,n,b,a);
            System.out.println(p+q);
        }
        in.close();
    }
    private static int Dijkster(int[][]Edge,int n,int start,int end){
        int[] dist=new int[n+1];//dist用来保存从起点到每个点的最短路径，到不了的点距离设置为无穷大
        int[]path=new int[n+1];//path用来保存每个点的前一个顶点号，如path[3]=2,则有顶点2-3
        boolean[] s=new boolean[n+1];//s用来记录该点是否已经确定了，初始化都为false,当把该点计入最短路径后，设为true;
        for(int i=1;i<=n;i++){//初始化dist,path
            dist[i]=Edge[start][i];
            if(i!=start&&dist[i]<Integer.MAX_VALUE){
                path[i]=start;
            }else{
                path[i]=-1;
            }
        }
        s[start]=true;//从第一个顶点开始计算
        dist[start]=0;
        for(int i=0;i<n;i++){
            int min=Integer.MAX_VALUE;
            int u=0;
            //选择当前未确定顶点中具有最短路径（离起点最近）的顶点u
            for(int j=1;j<=n;j++){
                if(!s[j]&&dist[j]<min){
                    u=j;
                    min=dist[j];
                }
            }
            //此时u已经在最短路径上了，更新s
            s[u]=true;
            for(int k=1;k<=n;k++){
                if(!s[k]&&Edge[u][k]<Integer.MAX_VALUE&&dist[u]+Edge[u][k]<dist[k]){
                    dist[k]=dist[u]+Edge[u][k];
                    path[k]=u;
                }
            }
        }
       return dist[end];

    }
}

运行测试了下，发现在数据量小的时候，代码是没问题的，也就是当端点数n<=100 算法均能正确运行

当n>100后，运行结果显示：

在int[][] Edge=new int[n+1][n+1];这句处

Exception in thread "main" java.lang.OutOfMemoryError: Java heap space

也就是内存超出了


也就说明这个时候应该换用 邻接表来表示图了