Kmp简单运用
一个简单的题,复习一下KMP
对于两个字符串A,B。请设计一个高效算法,找到B在A中第一次出现的起始位置。若B未在A中出现,则返回-1。
给定两个字符串A和B,及它们的长度lena和lenb,请返回题目所求的答案。
"acbc",4,"bc",2
返回:2
1 import java.util.*; 2 3 public class StringPattern { 4 public int findAppearance(String A, int lena, String B, int lenb) { 5 // write code here 6 return kmp(A,lena,B,lenb); 7 } 8 private int kmp(String A,int m,String B,int n){ 9 if(A==null||B==null||m==0||n==0) return -1; 10 int[] next=new int [n]; 11 makeNext(B,next); 12 int j=0; 13 for(int i=0;i<m;i++){ 14 while(j>0&&A.charAt(i)!=B.charAt(j)) //j>0表明此时前面已经有匹配成功的,只是在A串和B串在此处不同,所以j保持和前面一致 15 j=next[j-1]; 16 if(A.charAt(i)==B.charAt(j)) 17 j++; //如果能一直匹配成功的话,则j一直增加直到到达b串的末尾,表示匹配成功 18 if(j==n) 19 return i-j+1; 20 } 21 return -1; 22 23 } 24 public void makeNext(String B,int []next){ 25 //构造next表,如对于ABCDAB 为 0 0 0 0 1 2 26 //相当于对自己把自己同时当成文本串和字符串进行比较,字符串向后移动,每次都从0开始,有相同的就加1 开始比较下一位 27 //没有相同的就保持和原来一样 28 next[0]=0; 29 int j=0; 30 for(int i=1;i<B.length();i++){ 31 while(j>0&&B.charAt(i)!=B.charAt(j)) 32 j=next[j-1]; 33 if(B.charAt(i)==B.charAt(j)) 34 j++; 35 next[i]=j; 36 } 37 } 38 }
总结一下,kmp算法的核心就在于next[]数组,如果不用next[]数组的话,与暴力匹配没有什么不同,正是由于使用了next[]数组,使得当匹配失败时,我们可以利用失败的信息,减少不必要的匹配次数;
举个栗子:例如A串:BBC ABCDAB ABCDABCDABDE
要查找的B串:ABCDABD
如果是暴力匹配的话,
012345678910
BBC ABCDAB ABCDABCDABDE
ABCDABD
在B串匹配到D的时候,发生了匹配失败,此时B串的坐标j回退到开头位置0,A串的坐标i回退到5(即原来的下一位),然后从头开始继续匹配。但是,如果我们观察要查找的B串就会发现,在发生匹配失败时,失败前A串中前面位置的字符我们是知道的(因为前面匹配成功了,比如在这个例子中,D前面的“ABCDAB”与A串是已经匹配成功的,所以A串对应位置也必然是“ABCDAB”),所以我们就会知道,此时让A串回退到原来的下一位再继续与B串进行匹配,实质上就是B串与前面自己的匹配,所以我们可以看出如果B串中有重复的字符,那么就可以直接跳到重复的字符位置继续进行匹配,如果B串中没有重复的字符,那么代表着前面A串中必然没有能匹配成功的位置,直接让A串的i继续向后移动,寻找下一段能匹配的位置。
上面这段话是kmp算法的核心,再用这个例子进行一下解释
012345678910 BBC ABCDAB ABCDABCDABDE ABCDABD
可以看出,B串中的j直接跳到了A串中上次匹配成功的字符段中第二个字符‘A’的位置(即j=8),为什么j能直接跳到这个位置,而不用跳到5,6,7进行比较呢?因为字符串B的第二个A前面没有重复的字符,而前面匹配成功的A串与B串是一样的,所以B串中的开头“A”必然会与前面的“BCD”匹配失败,所以j 会直接跳到j=8继续进行比较,那么我如何知道每次失败时j该怎么选呢?这就是next[]数组所要提供的功能,如果失败,对于每个位置j有对应的next[j]去跳
next[]数组是怎么来的?就是对B串自己进行一次匹配,记下对于每个位置字符前面重复的字符个数
ABCDABD
0000122
可以得到数组[0000122]
再次回到刚才失败的地方
012345678910 BBC ABCDAB ABCDABCDABDE ABCDABD
0123456
在j=6的时候匹配失败如何让A与下一个A继续进行匹配呢,即到达这个位置
012345678910 BBC ABCDAB ABCDABCDABDE ABCDABD
012
由于A串此时不回退,即i=10保持不变,如果让j=2,此时等同于让B串向右移动,使‘A’与‘A’匹配上了
位置坐标 0123456
字符串 ABCDABD 数组 0000122
当j=6时发生了失败,我们此时考虑的是在j=6的位置前面的字符串里的字符重复情况,所以j=next[j-1];
相应的代码就为
for(int i=0;i<m;i++){ 14 while(j>0&&A.charAt(i)!=B.charAt(j)) //j>0表明此时前面已经有匹配成功的,只是在A串和B串在此处不同,所以j保持和前面一致 15 j=next[j-1]; 16 if(A.charAt(i)==B.charAt(j)) 17 j++; //如果能一直匹配成功的话,则j一直增加直到到达b串的末尾,表示匹配成功 18 if(j==n) 19 return i-j+1; 20 }
上面这种方法是利用B串中字符串的重复个数来求next[]数组,我觉得这种方法的代码很简洁,但是使用时要注意在j!=0时才能查数组,不然就会有j=next[-1]这种情况,相应的,这种构造next[]数组的方法就为
public void makeNext(String B,int []next){ 25 //构造next表,如对于ABCDAB 为 0 0 0 0 1 2 26 //相当于对自己把自己同时当成文本串和字符串进行比较,字符串向后移动,每次都从0开始,有相同的就加1 开始比较下一位 27 //没有相同的就保持和原来一样 28 next[0]=0; 29 int j=0; 30 for(int i=1;i<B.length();i++){ 31 while(j>0&&B.charAt(i)!=B.charAt(j)) 32 j=next[j-1]; 33 if(B.charAt(i)==B.charAt(j)) 34 j++; 35 next[i]=j; 36 } 37 }
当然,还有一种求next[]数组的方法是利用B串的最长前缀后缀来求,(感谢July的博客)
我们继续看
对于串ABCDABD
我们来求它的每个子字符串前后缀最大公共元素长度
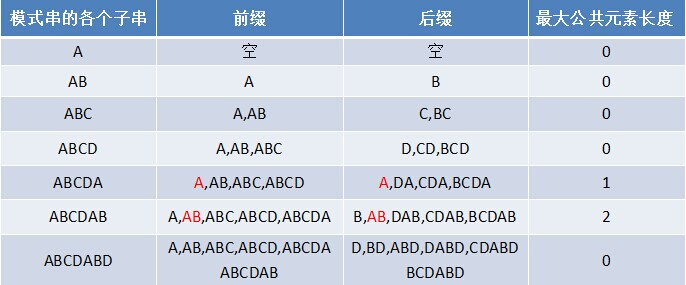
所以可以得到表

next 数组考虑的是除当前字符外的最长相同前缀后缀,所以通过前面求得各个前缀后缀的公共元素的最大长度后,只要稍作变形即可:将上表中求得的值整体右移一位,然后初值赋为-1,如下表格所示:
| A | B | C | D | A | B | D |
| -1 | 0 | 0 | 0 | 0 | 1 | 2 |
然后便可直接运用进行匹配
算法核心如下
1 int KmpSearch(char* s, char* p) 2 { 3 int i = 0; 4 int j = 0; 5 int sLen = strlen(s); 6 int pLen = strlen(p); 7 while (i < sLen && j < pLen) 8 { 9 //①如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++ 10 if (j == -1 || s[i] == p[j]) 11 { 12 i++; 13 j++; 14 } 15 else 16 { 17 //②如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j] 18 //next[j]即为j所对应的next值 19 j = next[j]; 20 } 21 } 22 if (j == pLen) 23 return i - j; 24 else 25 return -1; 26 }
而求next[]数组的代码如下
1 void GetNext(char* p,int next[]) 2 { 3 int pLen = strlen(p); 4 next[0] = -1; 5 int k = -1; 6 int j = 0; 7 while (j < pLen - 1) 8 { 9 //p[k]表示前缀,p[j]表示后缀 10 if (k == -1 || p[j] == p[k]) 11 { 12 ++k; 13 ++j; 14 next[j] = k; 15 } 16 else 17 { 18 k = next[k]; 19 } 20 } 21 }
对于这种求next[]数组的方法我们继续以串ABCDABD为例来理解
1.对于数组第一个值直接赋-1,很好理解即next[0]=-1 next[]={-1}
2.next[1]=0,这是因为j=1的前面只有一个字符,相同前后缀为0 next[]={-1,0}
3. 0123456
ABCDABD 此时由于 p[0]!=p[1],所以k=next[0]=-1
j
k
4. 0123456
ABCDABD k=-1满足条件,继续构造next[]数组;
j j=2,k=0, next[2]=0, next[]={-1,0,0}
k=-1
5.比较p[0]!=p[2],所以回退k,k=next[0]=-1
6.重置完后继续构造next[]数组
0123456
ABCDABD
j j,k向后移,k=0,j=3 next[3]=k=0 ,next[]={-1,0,0,0}
k=-1
7.比较p[0]!=p[3],继续回退k,k=next[0]=-1
8.构造数组
j,k向后移一位,k=0,j=4,next[4]=k=0,next[]={-1,0,0,0,0}
9.比较p[0]==p[4],所以此时k不用回退了
0123456
ABCDABD j,k向后移一位,j=5,k=1
j 所以此时,next[5]=k=1 next[]={-1,0,0,0,0,1}
k
10.比较p[1]==p[5]
所以,j,k向后移一位,j=6,k=2
所以此时,next[6]=k=2, next[]={-1,0,0,0,0,1,2}
如果我们仔细观察一下,上面这个过程,就能发觉,j,k在这里所起的作用
j的作用是用来遍历整个串的每个位置,而k是用来记录j的前面有没有相同的前后缀,如果有则记录它的长度,如果没有,则k回退,j移向下一位继续寻找
而next[j]所记录的其实是,j前面的字符串的相同前后缀的长度
k=-1其实就是一个标志,表明当前p[0]!=p[j],所以j需要移动到下一位
所以我们就可以看出
j=1时,对应子串为“AB”,由于p[0]!=p[1],无相同前后缀,所以对应的next[1]=0,next[1]记录的是串“A”的相同前后缀情况,为0
j=2时,对应子串为“ABC”,p[0]!=p[2],所以k=0,next[2]记录的是串“AB”的前后缀情况,故next[2]=0
同理,j=3时,子串“ABCD”p[0]!=p[3],k=0,next[3]记录的是串“ABC”的前后缀情况,故next[3]=0;
j=4时,对应子串“ABCDA”,p[0]==p[4],所以此时有相同前后缀了,k=1,next[4]记录的是串"ABCD”的前后缀情况,故next[4]=0
j=5时,对应子串“ABCDAB”p[1]==p[5],k=2,next[5]记录的是串“ABCDA”的前后缀情况,故next[5]=1
同理,j=5,对应子串“ABCDABD” p[2]!=p[6],k=0,再进行比较p[0]!=p[6],,k=-1,next[6]记录的是串“ABCDAB”的前后缀情况,故next[6]=2
以上是利用字符串的前后缀来求next[]数组,这种方法对于next[]数组还存有一定的改进之处
例如对于A串“ABCDABD”,B串“ABAB”进行匹配
B 串的next[]数组为next[]={-1,0,0,1}
0123456
ABCDABD
ABAB
0123
在j=2出发生了失败,此时根据next[]数组可移动j,得到j=next[2]=0
ABCDABD
ABAB
发现还是失败的,我们发现其实这一步是可以避免的,因为在前面一步的信息中我们就已经知道了A[2]='C'!='A',而B[0]==B[2]=='A',所以必定是不匹配的
这种情况之所以出现是因为在这个模式串中B[j]==B[next[j]],所以当模式串中出现这种情况时 ,我们应该单独考虑这种情况,此时让
j=next[next[j]]
1 while (j < pLen - 1) 2 { 3 //p[k]表示前缀,p[j]表示后缀 4 if (k == -1 || p[j] == p[k]) 5 { 6 ++k; 7 ++j; 8 if(p[j]!=p[k]){ 9 next[j] = k; 10 }else{ 11 next[j]=next[k]; 12 } 13 else 14 { 15 k = next[k]; 16 } 17 }
又碰到了 一道字符串模式匹配的题(来自leetcode):
就是自己实现c里面的strstr()函数(字符串查找),注意最后返回的是一个指针
Implement strStr().
Returns a pointer to the first occurrence of needle in haystack, or null if needle is not part of haystack.
分析:一般而言,这类题就是考察kmp算法的,但是看到有人还用了Sunday算法等其他算法
还有排名第一的这个算法,这是个啥算法,怎么能这么快,给出他的代码,我后天有门考试,还没复习完,没时间只能先把该题的链接存下,等我有时间了好好研究一下这些妖娆的算法,并试着用用sunday,和bM算法ac一下这道题,今天就到这里吧。
1 public class Solution 2 { 3 4 public String strStr(String s, String t) 5 { 6 if(s==null || t==null) return null; 7 if(t.length() == 0) return s; 8 int lenS = s.length(); 9 int lenT = t.length(); 10 for(int i=0; i<=lenS-lenT; i++) 11 { 12 int j = 0; 13 for(; j<lenT; j++) 14 { 15 if(s.charAt(i+j) != t.charAt(j)) break; 16 } 17 if(j == lenT) return s.substring(i); 18 } 19 return null; 20 } 21 }
下面这个题,来看一下sunday算法,他的介绍如下:July的博客
Sunday算法由Daniel M.Sunday在1990年提出,它的思想跟BM算法很相似:
- 只不过Sunday算法是从前往后匹配,在匹配失败时关注的是文本串中参加匹配的最末位字符的下一位字符。
- 如果该字符没有在模式串中出现则直接跳过,即移动位数 = 匹配串长度 + 1;
- 否则,其移动位数 = 模式串中最右端的该字符到末尾的距离+1。
下面举个例子说明下Sunday算法。假定现在要在文本串"substring searching algorithm"中查找模式串"search"。
1. 刚开始时,把模式串与文本串左边对齐:
substring searching algorithm
search
^
2. 结果发现在第2个字符处发现不匹配,不匹配时关注文本串中参加匹配的最末位字符的下一位字符,即标粗的字符 i,因为模式串search中并不存在i,所以模式串直接跳过一大片,向右移动位数 = 匹配串长度 + 1 = 6 + 1 = 7,从 i 之后的那个字符(即字符n)开始下一步的匹配,如下图:
substring searching algorithm
search
^
3. 结果第一个字符就不匹配,再看文本串中参加匹配的最末位字符的下一位字符,是'r',它出现在模式串中的倒数第3位,于是把模式串向右移动3位(r 到模式串末尾的距离 + 1 = 2 + 1 =3),使两个'r'对齐,如下:
substring searching algorithm
search
^
4. 匹配成功。
回到上面的那个题,我们可以写出代码
1 public class Solution { 2 public String strStr(String haystack, String needle) { 3 return sunday(haystack,needle); 4 } 5 private static String sunday(String A,String B){ 6 int m=A.length(); 7 int n=B.length(); 8 if(m==0&&n==0)return ""; 9 if(n==0)return A; 10 int[] back=new int[256]; 11 for(int i=0;i<256;i++){ 12 back[i]=n; 13 } 14 for(int i=0;i<n;i++){ 15 //记录B串中每个字符从后往前的位置,如有重复的记下第二次的位置 16 back[B.charAt(i)]=n-i; 17 } 18 int j=0; 19 while(j<=m-n){ 20 int i=0; 21 while(i<n&&A.charAt(i+j)==B.charAt(i)) 22 i++; 23 if(i==n)return A.substring(j); 24 else{ 25 if(j+n>=m) break; 26 j+=back[A.charAt(j+n)]; 27 } 28 } 29 return null; 30 } 31 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号