LeetCode137 Single Number II 只出现一次的数字 II

• 题目描述

　　给定一个非空整数数组，除了某个元素只出现一次之外，其余每个元素都出现了三次，找出那个只出现一次的元素。

　　说明：算法应该具有线性时间复杂度，并且不使用额外空间。

• 分析

　　首先，假如说题目没有说明里面的要求，那么就非常简单，可以使用一个map用来存储元素和元素出现的次数，遍历完数组之后，遍历这个map，就可以找到只出现一次的元素。此时时间复杂度为O(n)，空间复杂度为O(n)。而说明要求空间复杂度为O(1)，不满足。需要另寻它法。

　　如果出现多次的元素，其次数不是3，而是2，那么这个问题相信也就难不倒大部分人了。此时，可以利用位运算，利用异或运算其“同零异一”的特性，来解决问题。比如数组只有三个元素：2,2,3. 三个数字的二进制表示为：10,10,11。那么对三个数进行异或运算，出现两次的数，在对应的bit位上，由于“同零”的特性，变为0，那么所有的出现两次的数字异或运算后的结果就是零；而只出现一次的数字，其与零异或运算的结果就是它自身。如上例中10,10,11的异或运算结果是11，就是“3”这个数字本身。因此可以很简洁地写出代码。

int singleNumber(vector<int>& nums) {
        int a=0;
        for(auto n:nums) a^=n;
        return a;
    }

　　但是题目中的条件是其余每个元素都出现了三次。

　　我们仍然延续位运算的思想。

　　考虑数组9,7,7,7，其二进制表示为：1001,0111,0111,0111。分别统计 从左到右四个bit位上的0和1分布情况。最高位，1出现了1次；第二位，1出现了3次；第三位，1出现了3次；最低位，1出现了4次。很容易发现，中间两位1出现的次数为3的倍数，这两位也只在数字7的二进制表示中出现，而不在9的二进制表示中出现；最高位和最低位1出现的次数模3的余数为1，这两位都在9的二进制表示中出现。

　　因此，可以得出结论，在此题的背景下，统计所有数组所有int型元素在32个bit位上出现1的数目，如果某个位上1出现的次数模3余数为1，那么1一定在那个“唯一”的数字中出现；反之，某个位上1出现的次数为3的整数倍，那么1一定不在“唯一”的数字中出现。据此，可以写出代码。

int singleNumber(vector<int>& nums) {
        vector<int> cnt(32,0);
        for(auto n:nums)
        {
            for(int i=0;i<32;i++)
            {
                if(n&1) cnt[i]++;
                n>>=1;
            }
        }
        int ans=0;
        for(int i=0;i<32;i++)
        {
            if(cnt[i]%3) ans+=1<<i;
        }
        return ans;
    }

　　上面的代码在LeetCode上能AC，时间复杂度O(n)，空间复杂度O(1)。

　　但是还可以更快吗？像上面的直接使用异或运算那样？

　　上面的算法我们记录了32个bit位上每一个位置1出现的次数，实际上我们需要的是1出现的次数模3的余数值。模3的结果只能有0,1,2，换成二进制表示是00,01,10. 因此我们可以用两个int型数字a和b来记录所有bit位的信息。例如，a的最后一位bit位值为0，b的最后一位bit位的值为1，那么两者联合起来表示的意思就是：数组所有的数在最后一位bit位出现1的次数之和模3的余数是01，即1。其他bit位类推。

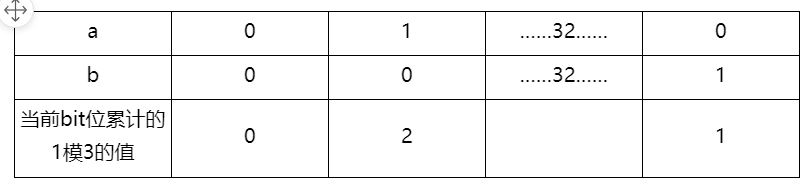
　　下面我们的目标就是，找到a和b和数组元素的某种位运算组合，使得a，b能完整地表达出我们需要的信息。

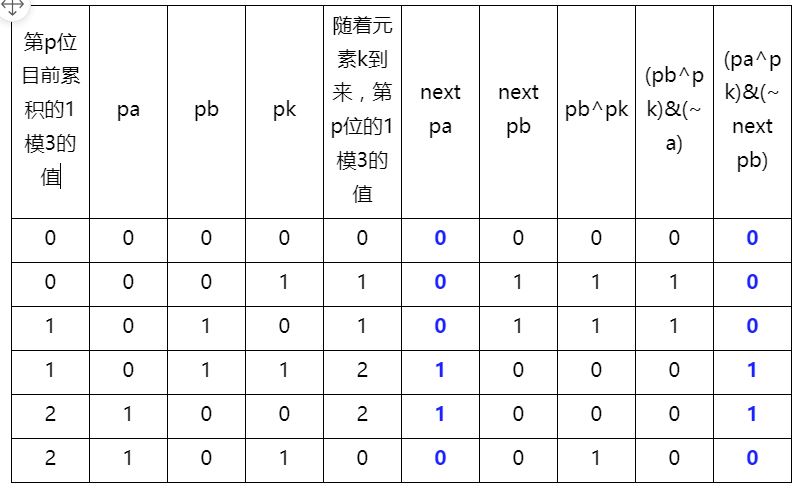
　　假设这种运算已经进行到数组第k-1个元素，数组下一个元素为k。此时a和b中某一个bit位——任意的一位，假设是从最低位往最高位数，第p=10位——的值分别为pa，pb。元素k的第10位值为pk。pa，pb，pk的取值无非就是0或者1。对于新来的元素k，根据pk的取值，pa，pb也需要发生相应的变化。见下图

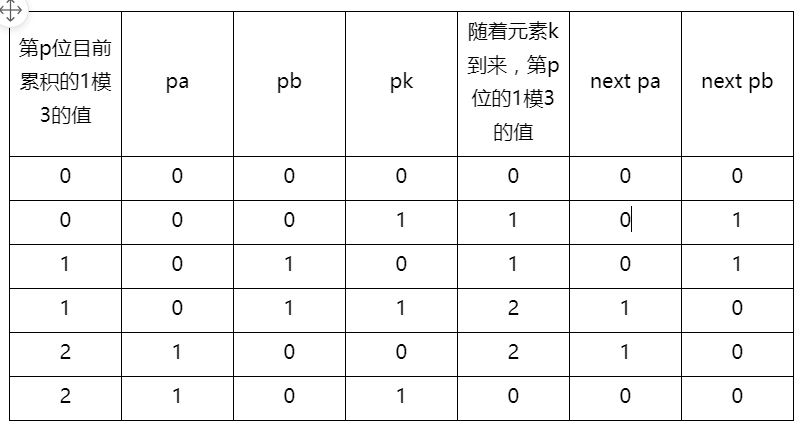
　　如上图所示，目标明确了：找到某种pa，pb，pk之间的位运算，使得pa，pb分别编程next pa和next pb。

　　我们可以先看pb和pk。首先看一下pb和pk异或运算的结果。

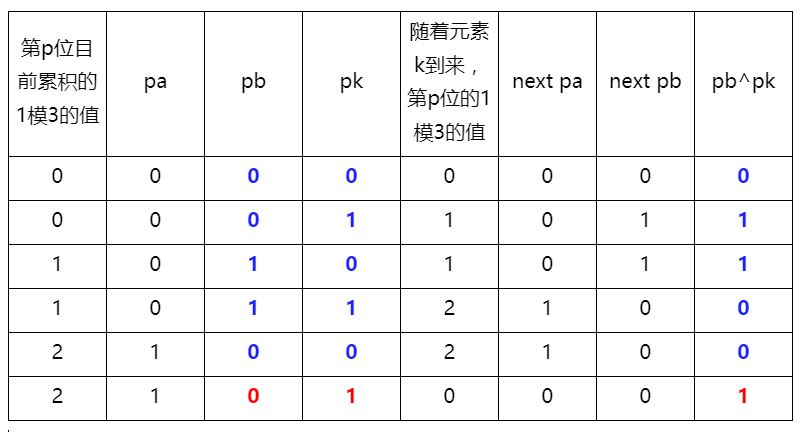
　　可以看到，前面5种情况，pb^pk的值和next pb一致，只有最后一种情况不一致。说明仅仅依靠pb^pk是不够的。我们发现，a的信息还没有利用。最后一种情况下，pb^pk=1，pa=1，目标是pb^pk与pa的某种位运算得到next pb=0。尝试一下，我们发现此时，(pb^pk)&(~a)=next pb。计算一下其他几种情况下是否也满足。

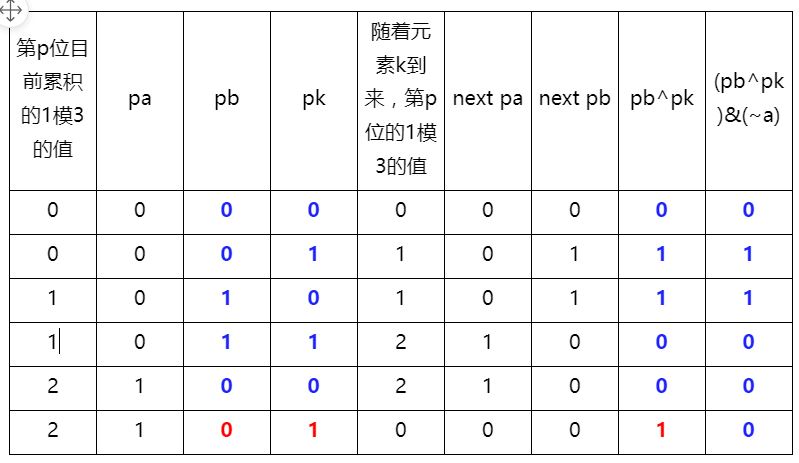
　　计算发现，此时next pb = (pb^pk)&(~a)！

　　同理我们可以根据pa，pk和pb组合出next pa的结果。经过推理尝试，发现next pa = (pa^pk)&(~next pb)

　　上述推导出的bit运算对32个bit位都适用，于是最终得到公式：

　　b=(b^k)&(~a);

　　a=(a^k)&(-b);

　　对数组中的元素依次进行上式的运算，最后，我们想求得只出现一次的数，就是每个bit位上1出现的次数之和模3余1的bit位组成的数，那就是b。代码如下

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int a=0,b=0;
        for(auto n:nums)
        {
            b=(b^n)&(~a);
            a=(a^n)&(~b);
        }
        return b;
    }
};

　　上面的代码在LeetCode能AC。

　　那么，a和b只有上面这一种组合位运算能得到next a和next b吗？其实有很多种，比如笔者就发现了下面另外一种：

　　a=((b&n)^n)^(a&~b);
　　b=(b^n)^(a&n);

int singleNumber(vector<int>& nums) {
        int a=0,b=0;
        for(auto n:nums){
            a=((b&n)^n)^(a&~b);
            b=(b^n)^(a&n);
        }
        return a;
    }

　　上面的代码同样AC。

　　更多的方法等你去发现和总结。