求解四只鸭子在同一半圆池塘的概率
- 问题模型
有四只鸭子,随机分布在圆形的池塘中,请问四只鸭子同时处于同一个半圆的概率有多大?
- 统计模拟
使用计算机进行大量的随机实验,统计推断出未知变量的概率。我们将进行100万次独立采样试验,每次试验中让四只鸭子随机分布在圆形池塘中,统计四只鸭子处于同一半圆的试验次数。那么使用该次数除以100万,就可以大概得到题目所求的概率。
- 建立模型
假设以原点为中心,半径为1的单位圆即为问题里的池塘,四只鸭子为出现在单位圆内部随机位置的四个点,那么这四个点位于同一半圆内的概率即为题目所求的概率值。
- 怎么判断四个点位于同一个半圆?
四个点可能一下子有点抽象,那么不妨将问题弱化:考虑从四个点变为三个点的情况。怎么判断三个点位于同一个半圆?
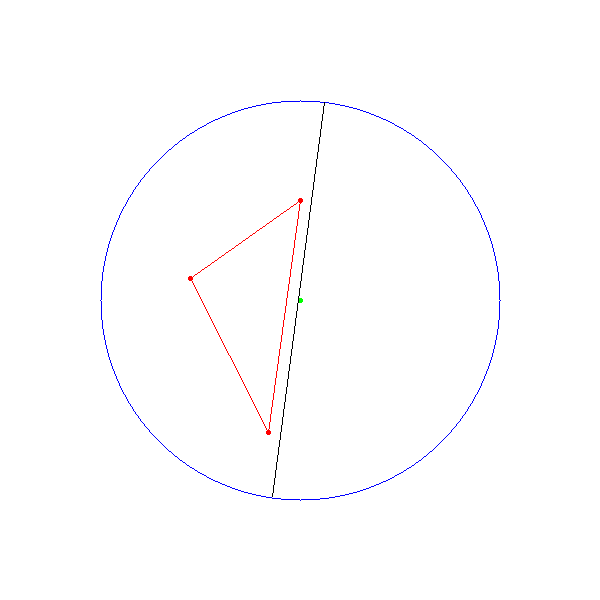
如上图所示,在圆中有三个点,我们可以画出三个点组成的三角形的三条边,不难发现,圆的圆心在三角形的外边,这时我们一定可以找到圆的一条直径,将三角形分在圆的某个半圆中。
那如果圆心在三个点组成的三角形内部呢,能找到一条直径将三个点分在同一个半圆吗?稍微在头脑中模拟一下,不难想到,答案是否定的。如下图所示,无论怎样选取直径,都不能将三个点分到同一个半圆中。
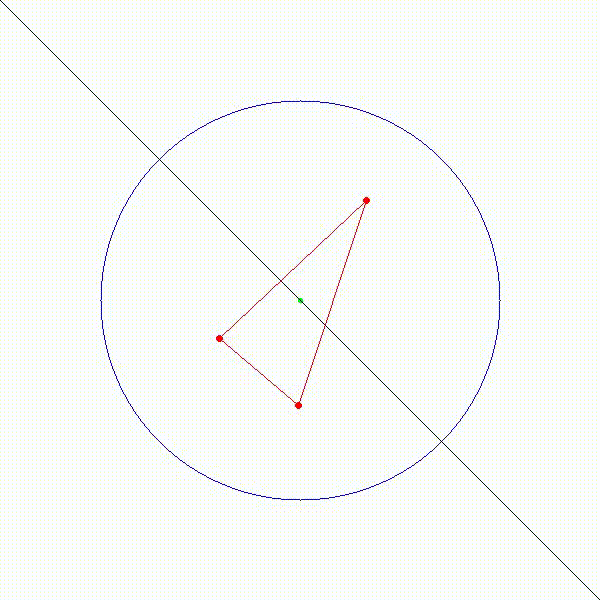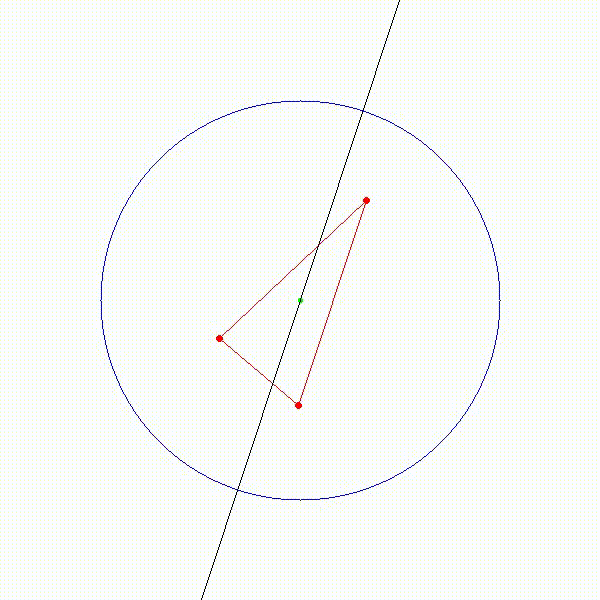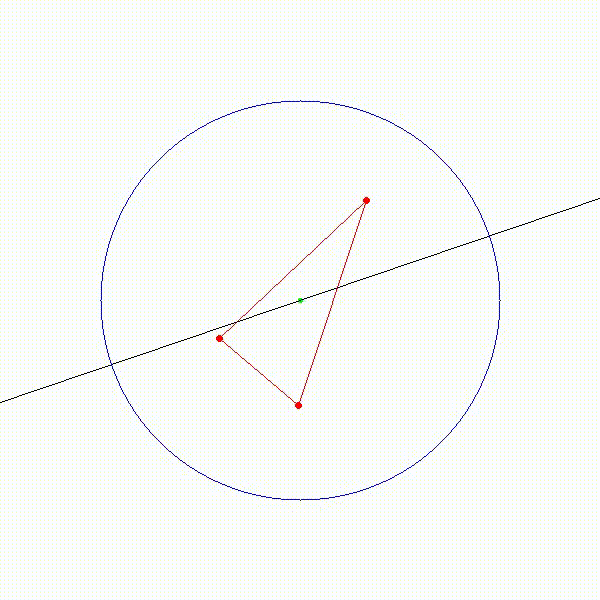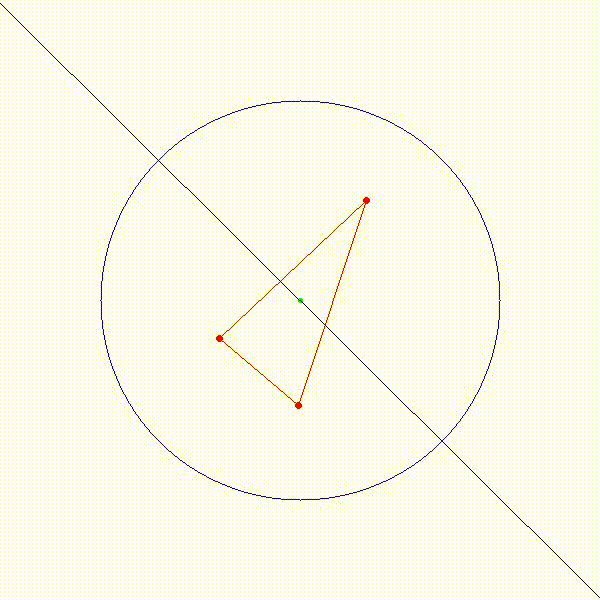
于是我们可以得到一个结论,只要圆心位于三角形外,就一定能将三角形分在同一个半圆中。
- 那么推广到四个点的情况,结论会是怎样的?
首先,如果圆中随机分布的四个点共半圆,那么这四个点中的任意三个也一定共半圆,这个很容易理解。那么结论反过来成立吗?也就是说,圆中有四个点,任意三个点都共半圆,那么这四个点一定共半圆吗?
我们可以使用反证法。
假设存在圆中有四个点,其中任意三个点都共半圆,但是四个点不共半圆的情况。不失一般性,我们假设四个点为a,b,c,d。如下图所示,我们画出a,b,c点和经过这三个点的圆直径。
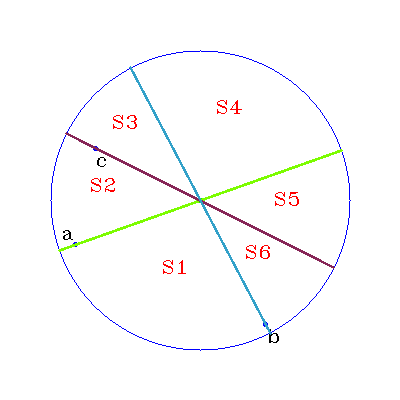
三条直径将圆分为了6个区域,分别为S1~S6。现在我们考虑将第四个点放在什么地方,可以满足任意三个点共半圆,但是四个点不共半圆的情况。
如果d点放在区域S1,S2或者S3,显然,abcd共蓝色直径左边的半圆,矛盾;
如果d点放在区域S6,显然,abcd共紫色半径下方的半圆,矛盾;
如果d点放在区域S4,此时abcd不共半圆,但是此时abd点也不共半圆,与假设任意三个点共半圆,矛盾;
如果d点放在区域S5,此时abcd不共半圆,但是此时acd点也不共半圆,与假设任意三个点共半圆,矛盾。
综上,d点无论放在哪个区域,都不满足假设的条件,因此假设不成立!
因此我们得到结论,圆内随机分布的四个点,如果其中任意三个点都共半圆,那么这四个点也一定共半圆。
于是我们得到了判断四只鸭子位于池塘的同一半圆区域的判别条件。
- 判断点在三角形外部的方法
判断一个点在三角形外部还是内部有很多种方法,我常用的是两种,一种是内角和法:如果点在三角形内部,那么该点与三角形的三个顶点形成的三个角的和为360度,反之,如果点在三角形外部,那么三个角之和一定小于360度。
第二种是同向法。对于三角形Δabc,如果点p在三角形内部,那么对于三角形的每条边构成的向量——例如向量ab——来说,其另外一个顶点c与该边的起始点a构成的向量ca,这两个向量的叉积方向与向量pa和向量ab的叉积方向是一致的,从数值上的表现来看,要么同为正值,要么同为负值。对于向量bc,向量ca的情况,结果也是一致的。而对于在三角形外部的点q来说,至少有一条边的情况不满足叉积方向一致。
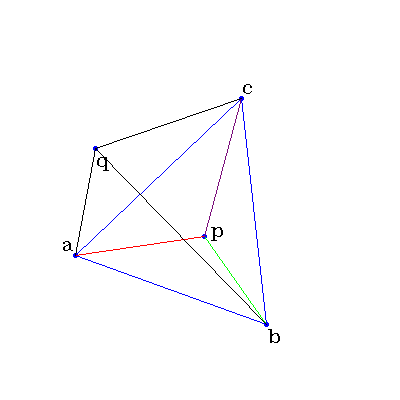
如上图中的例子,先看三角形内部的点p。对于边ab来说,向量ab叉乘向量ca,根据右手定则,叉积的方向指向屏幕里面,向量ab叉乘向量pa,根据右手定则,叉积的方向指向屏幕里面,两个叉积方向一致;对于边bc来说,向量bc叉乘向量ab,根据右手定则,叉积的方向指向屏幕里面,向量bc叉乘向量pb,根据右手定则,方向指向屏幕里面,两个叉积方向一致;对于边ca来说,向量ca叉乘向量bc,根据右手定则,方向指向屏幕里面,ca叉乘pc,方向同样是指向屏幕里面。因此可以判断点p在三角形内部。
而对于q点,我们可以直接看边ca,向量ca与向量bc的叉乘方向指向屏幕里面,但是向量ca与向量qc叉乘,根据右手定则,叉积的方向指向屏幕外面,两者方向不一致,可以判断q点在三角形外部。
我们可以从数值上来验证这个结论。对于二维向量a(ax,ay)和b(bx,by),其叉积的数值为ax*by-bx*ay。对于笔者所画的上图,如果以左下角为坐标原点,正右方向为x轴方向,正上方向为y轴方向,单个像素为单位长度的话,各点的坐标如下:
a(75, 145), b(266, 76), c(241, 302), p(204, 164), q(95, 252)
先看边ab,
ab X ca = (191, -69) X (-166, -157) = 191 * (-157) - (-69) * (-166) = -41441
ab X pa = (191, -69) X (-129, -19) = 191 * (-19) - (-129) * (-69) = -12530
ab X qa = (191, -69) X (-20, -107) = 191 * (-107) - (-20) * (-69) = -21887
三个叉乘的方向一致,再看边bc
bc X ab = (-25, 226) X (191, -69) = -25 * (-69) - 226 * 191 = -44891
bc X pb = (-25, 226) X (62, -88) = -25 * (-88) - 226 * 62 = -11812
bc X qb = (-25, 226) X (171, -176) = -25 * (-176) - 226 * 171 = -34246
三个叉乘方向一致,最后看边ca,
ca X bc = (-166, -157) X (-25, 226) = -166 * 226 - (-25) * (-157) = -41441
ca X pc = (-166, -157) X (37, 138) = -166 * 138 - 37 * (-157) = -17099
ca X qc = (-166, -157) X (146, 50) = -166 * 50 - 146 * (-157) = 14622
向量ca与向量bc的叉积方向和向量ca与向量pc的叉积方向一致,但是和向量ca与向量qc的叉积方向不一致。所以得出结论,点p在三角形abc内部,而点q在外部。
详细的论述请参考链接http://www.blackpawn.com/texts/pointinpoly/default.html
综上,我们已经得到了求解题目的所有步骤。
- 代码
使用同向法判断点在三角形外部代码
1 bool beyondTriangle(Point2f& a, Point2f& b, Point2f& c, Point2f& p) 2 { 3 Point2f ab = Point2f(b.x - a.x, b.y - a.y); 4 Point2f ca = Point2f(a.x - c.x, a.y - c.y); 5 Point2f pa = Point2f(a.x - p.x, a.y - p.y); 6 double cross_ca_ab = ca.x * ab.y - ab.x * ca.y; 7 double cross_pa_ab = pa.x * ab.y - ab.x * pa.y; 8 double orientation = cross_ca_ab * cross_pa_ab; 9 if (orientation < 0) return true; 10 Point2f bc = Point2f(c.x - b.x, c.y - b.y); 11 Point2f pb = Point2f(b.x - p.x, b.y - p.y); 12 double cross_ab_bc = ab.x * bc.y - bc.x * ab.y; 13 double cross_pb_bc = pb.x * bc.y - bc.x * pb.y; 14 orientation = cross_ab_bc * cross_pb_bc; 15 if (orientation < 0) return true; 16 Point2f pc = Point2f(c.x - p.x, c.y - p.y); 17 double cross_bc_ca = bc.x * ca.y - ca.x * bc.y; 18 double cross_pc_ca = pc.x * ca.y - ca.x * pc.y; 19 orientation = cross_bc_ca * cross_pc_ca; 20 if (orientation < 0) return true; 21 return false; 22 }
求解的主要代码如下:
double calcFourDuckInCirclePoolPolarCoordinates() { int PIECE = 36000; int REGION = 100000; int ITER = 1000000; double PI = acos(-1); uniform_int_distribution<unsigned> theta_d(0, PIECE); uniform_int_distribution<unsigned> r_d(0, REGION); default_random_engine theta_e((unsigned int)time(NULL)); default_random_engine r_e(0); vector<Point2f> pos; pos.resize(4); int candies = 0; Point2f center(0.f, 0.f); for (int i = 0; i < ITER; ++i) { for (int duck = 0; duck < 4; ++duck) { auto theta_ = theta_d(theta_e); auto r_ = r_d(r_e); double theta = ((double)theta_ / 100.0 - 180) / 180 * PI; double r = (double)r_*1.0 / REGION; double x = r * cos(theta); double y = r * sin(theta); pos[duck] = Point2f(x, y); } if (!beyondTriangle(pos[0], pos[1], pos[2], center)) continue; if (!beyondTriangle(pos[0], pos[1], pos[3], center)) continue; if (!beyondTriangle(pos[0], pos[2], pos[3], center)) continue; if (!beyondTriangle(pos[1], pos[2], pos[3], center)) continue; ++candies; } double probability = candies*1.0 / ITER; cout << "probability: " << fixed << setprecision(5) << candies*1.0 / ITER << endl; return probability; }
- 结果
多次的采样实验结果显示,通过统计模拟求解四只鸭子位于池塘同一个半圆的概率的答案为0.5!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号