数学公式/定理/板子整理

1.各种数：

　　全排列：P(n,n)=n!    部分排列：P(n,m)=n!/(n-m)!

　　组合数：公式：C(n,m)=n!/(m!*(n-m)!)   递推式 :C(n,m)=C(n-1,m)+C(n-1,m-1)  

　　　　　　Lucas定理：C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p

　　　　　　

#define long long LL 
//farc[i]表示i！ 
LL C(LL n,LL m,LL p){
    if(n<m)return 0;
    return farc[n]*fpow(farc[m],p-2,p)%p*fpow(farc[n-m],p-2,p)%p;
}
LL Lucas(LL n,LL m,LL p){
    if(n<m)return 0;
    if(!n)return 1;
    return Lucas(n/p,m/p,p)*C(n%p,m%p,p)%p;
}

　　　　　　性质/应用：1.C(n,m)=C(n,n-m)

　　　　　　 　　　　　2.二项式定理：

　　　　　　　　　　　 3.m*C(n,m)=n*C(n-1,m-1)，

　　　　　　　　　　　 4.C(n,1)²+C(n,2)²+C(n,3)²+...+C(n,n)²=C(2n,n)

　　圆排列: Q(n,n)=（n-1)!   n个人坐成一圈有多少种坐法。

　　　　　  Q(n,m)=P(n,m)/m=n!/(m*(n-m)!)   部分圆排列　　

　　重复排列(有限个)：n!/(a1!*a2!*…*ak!)  k种不一样的球，每种球的个数分别是a1,a2,...ak,设n=a1+a2+…+ak，求这n个球的全排列数。

　　重复组合(无限个):  C(n+k-1,k) 　　　  n种不一样的球，每种球的个数是无限的，从中选k个出来的方案数。

　　不相邻组合：C(n-k+1,k)  1~n这n个自然数中选k个，这k个数中任何两个数不相邻数的组合有多少种。

　　错排(错位排列)：d(n)=(n-1)*(dn-1 + dn-2)，n≥3

　　stirling数: 第一类：S(n,m)=S(n-1,m-1)+(n-1)*S(n-1,m)    n个不同元素构成m个圆排列的方案数

　　　　　　　第二类：S(n,m)=S(n-1,m-1)+m*S(n-1,m).       n个不同元素构成m个非空的(无差别)集合的方案数

　　Catalan数：通项式：H(n)=C(2n,n)/(n+1)=(2n)!/( (n+1)!*n!)

　　　　　　　　　　　  Hn=C(2n,n)-C(2n,n-1)

　　　　　　　  递推式：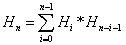

 

 

　　部分转载自：https://www.cnblogs.com/ljc20020730/p/11302718.html　　　

　　　　　　　　https://blog.csdn.net/qq_36808030/article/details/75045129　

2.数论：　　　　　　　阶:

　　　　　　　　　　   原根：

 

　　　　　　　　　　　常见的数的原根： 998244353：3       1e9+7：5       19260817：15 

 

　　部分转载自：https://www.cnblogs.com/zwfymqz/p/8244902.html#_label2_6

2.群论：　　　　　　　轨道稳定子定理：设G是[1,n]上的一个置换群，Ek是[1,n]在G的作用下包含k的等价类，Zk是k不动置换类。有|Ek||Zk|=|G|.

　　　　　　　　　　　拉格朗日定理：设H是有限群G的子群，则H的阶整除G的阶

　　　　　　　　　　　Burnside引理：对于一个置换f,若一个染色方案s经过置换后不变，称s为f的不动点。将f的不动点数目记为C(f)，则可以证明等价类数目为所有C(f)的平均值。

　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　polya引理：假设一个置换有k个循环，易知每个循环对应的所有位置颜色需一致，而任意两个循环之间选什么颜色互不影响。

　　　　　　　　　　　　　　　　  因此，如果有m种可选颜色，则该置换对应的不动点个数为m^k。用其替换burnside引理中的C(f)，得到等价类数目为：

　　　　　　　　　　　　　　　　  

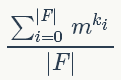
　　　　　　　　　　　　　　　　  其中|F|表示置换的数目，k_i表示第i个置换包含的循环个数　　

　　　　　　　　　　一些群论好题：polya引理模板 burnside引理好题 polya好题

　　部分转载自： https://www.cnblogs.com/beisong/p/4767858.html　　

3.线性代数：

　　1.矩阵：

　　　　加减乘除快速幂模板

struct mat {
  long long ma[sz][sz];
  mat() { memset(ma, 0, sizeof ma); }
}a,b,c;
mat operator+(const mat &A,const mat &B){
    mat res;
    for (int i = 0; i < sz; ++i)
      for (int j = 0; j < sz; ++j)
        res.ma[i][j] = (A.ma[i][j] + B.ma[i][j] + p) % p;
    return res;
}
mat operator-(const mat &A,mat &B) {
    mat res;
    for (int i = 0; i < sz; ++i)
      for (int j = 0; j < sz; ++j) res.ma[i][j] = (A.ma[i][j] - B.ma[i][j]) % p;
    return res;
}
mat operator*(mat &A,mat &B) {
    mat res;
    for (int i = 0; i < sz; ++i)
        for (int j = 0; j < sz; ++j)
            for (int k = 0; k < sz; ++k)
                res.ma[i][j] = (res.ma[i][j] + A.ma[i][k] * B.ma[k][j]) % p;
    return res;
}
mat operator^(mat &A,long long &x){
    mat res, bas;
    for (int i = 0; i < sz; ++i) res.ma[i][i] = 1;
    for (int i = 0; i < sz; ++i)
      for (int j = 0; j < sz; ++j) bas.ma[i][j] = A.ma[i][j];
    while (x) {
      if (x & 1) res = res * bas;
      bas = bas * bas;
      x >>= 1;
    }
    return res;
}

 

　　2.向量/复数：

struct Complex
{
    double x,y;
    Complex(){}
    Complex(double _x,double _y)
    {
        x=_x;
        y=_y;
    }
};
Complex operator +(const Complex &a,const Complex &b)
{
    return Complex(a.x+b.x,a.y+b.y);
}
Complex operator -(const Complex &a,const Complex &b)
{
    return Complex(a.x-b.x,a.y-b.y);
}
Complex operator *(const Complex &a,const Complex &b)
{
    return Complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);
}

　　　　单位根：在代数中，若zⁿ=1，我们把z称为n次单位根

　　　　　　　　在复平面上，以原点为圆心，1为半径作圆，所得的圆叫单位圆。以圆点为起点，圆的n等分点为终点，做n个向量，设幅角为正且最小的向量对应的复数为ω_n，称为n次单位根。

　　　　　　　　性质：1.  2.   

　　部分转载自：https://www.cnblogs.com/zwfymqz/p/8244902.html#_label2_6

 

4.多项式：

　　多项式的一些性质：1.卷积：系数表达：ci=∑ⁱ_j=0 a_j*b_i-j    点值表达：ci=a_i*b_i   

　　FFT板子：

#include<bits/stdc++.h>
using namespace std;
const double Pi = acos(-1.0);
const int MAXN = 1e7 + 7;
int n, m, limit = 1, r[MAXN], L, l, N, M;
inline int read(){
    int res = 0, f = 1;
    char c = getchar();
    while(c < '0' || c > '9'){if(c == '-')f = -1; c = getchar();}
    while(c >= '0' && c <= '9'){res = res * 10 + c - '0', c = getchar();}
    return res * f;
}
struct Complex{
    double x, y;
    Complex (double xx = 0, double yy = 0) {x = xx, y = yy;}
} a[MAXN], b[MAXN];
Complex operator + (Complex a, Complex b){return Complex(a.x + b.x, a.y + b.y);}
Complex operator - (Complex a, Complex b){return Complex(a.x - b.x, a.y - b.y);}
Complex operator * (Complex a, Complex b){return Complex(a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x);}
void FFT (Complex *A, int type){
    for(int i = 0; i < limit; i++){
        if(i < r[i])swap(A[i], A[r[i]]);
    }
    for(int mid = 1; mid < limit; mid <<= 1){
        Complex WN = Complex (cos(Pi / mid), type * sin(Pi / mid));
        for(int len = mid << 1, l = 0; l < limit; l += len){
            Complex W = Complex (1, 0);
            for(int k = 0; k < mid; k++, W = W * WN){
                Complex x = A[l + k], y = W * A[l + k + mid];
                A[l + k] = x + y;
                A[l + k+ mid] = x - y;
            }
        }
    }
}
int main() {
    n = read();
    m = read();
    for(int i = 0; i <= n; i++){
        a[i].x = read();
    }
    for(int i = 0; i <= m; i++){
        b[i].x = read();
    }
    while(limit <= n + m){
        limit <<= 1;
        L++;
    }
    for(int i = 0; i < limit; i++){
        r[i] = (r[i >> 1] >> 1) | ((i & 1) << (L - 1)); 
    }
    FFT(a, 1);
    FFT(b, 1);
    for(int i = 0; i <= limit; i++){
        a[i] = a[i] * b[i];
    }
    FFT(a, -1);
    for(int i = 0; i <= n + m; i++){
        printf("%d ", (int)(a[i].x / limit + 0.5));
    }
} 

#include <bits/stdc++.h>
using namespace std;
const double Pi=acos(-1);
const int MAX_N=1<<21;
struct Complex
{
    double x,y;
    Complex(){}
    Complex(double _x,double _y)
    {
        x=_x;
        y=_y;
    }
};
Complex operator +(const Complex &a,const Complex &b)
{
    return Complex(a.x+b.x,a.y+b.y);
}
Complex operator -(const Complex &a,const Complex &b)
{
    return Complex(a.x-b.x,a.y-b.y);
}
Complex operator *(const Complex &a,const Complex &b)
{
    return Complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);
}
Complex A[MAX_N],B[MAX_N],C[MAX_N];
int n,m; 
int ans[MAX_N],r[MAX_N],limit=1,L; 
void FFT(Complex A[],int flag)
{
    for(int i=0;i<limit;i++)
    {
        if(r[i]>i)swap(A[i],A[r[i]]);
    }
    for(int mid = 1; mid < limit; mid <<= 1){
        Complex WN = Complex (cos(Pi / mid), flag * sin(Pi / mid));
        for(int len = mid << 1, l = 0; l < limit; l += len){
            Complex W = Complex (1, 0);
            for(int k = 0; k < mid; k++, W = W * WN){
                Complex x = A[l + k], y = W * A[l + k + mid];
                A[l + k] = x + y;
                A[l + k+ mid] = x - y;
            }
        }
    }
    if(flag==-1)for(int i=0;i<limit;i++)A[i].x/=limit;
}
int main()
{
    string s1,s2;
    cin>>s1>>s2;
    int n=s1.size()-1,m=s2.size()-1;
    for(int i=0;i<=n;i++)A[i].x=s1[n-i]-'0';
    for(int i=0;i<=m;i++)B[i].x=s2[m-i]-'0';
    while(limit <= n + m){
        limit <<= 1;
        L++;
    }
    for(int i = 0; i < limit; i++){
        r[i] = (r[i >> 1] >> 1) | ((i & 1) << (L - 1)); 
    }
    FFT(A,1);
    FFT(B,1);
    for(int i=0;i<limit;i++)C[i]=A[i]*B[i];
    FFT(C,-1);
    for(int i=0;i<=n+m;i++)ans[i]=(int)(C[i].x+0.5);
    for(int i=0;i<=n+m;i++)
    {
        ans[i+1]+=ans[i]/10;
        ans[i]%=10;
    }
    for(int i=n+m+(ans[n+m+1]!=0);i>=0;i--)cout<<ans[i];
    cout<<endl;
    return 0;
}

 　  NTT板子：

#include<bits/stdc++.h>
using namespace std;
const int p=998244353;
const int D=3;
const int inD=332748118;
long long a[10000100],b[10000100],c[10000010];
int r[10000010];
int n,m,L;
inline int read(){
    char c=getchar();int f=1,res=0;
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){res=res*10+c-'0';c=getchar();}
    return f*res;
}
long long pw(long long a,long long b){
    long long res=1;
    while(b){
        if(b&1)res=res*a%p;
        a=a*a%p;
        b>>=1;
    }
    return res;
}
int limit=1;
void NTT(long long *A,int type){
    for(int i=0;i<limit;i++){
        if(i<r[i])swap(A[i],A[r[i]]);
    }
    for(int mid=1;mid<limit;mid<<=1){
        long long WN=pw((type==1?D:inD), (p-1)/(mid<<1));
        for(int l=0;l<limit;l+=(mid<<1)){
            long long W=1;
            for(int k=0;k<mid;k++,W=(W*WN)%p){
                long long x=A[l+k],y=(W*A[l+k+mid])%p;
                A[l+k]=(x+y)%p;
                A[l+k+mid]=(x-y+p)%p;
            }
        }
    }
    if(type==-1){
        long long inv=pw(limit, p-2);
        for(int i=0;i<limit;i++){
            A[i]=A[i]*inv%p;
        }
    }
}
int main(){
    n=read();
    m=read();
    for(int i=0;i<=n;i++){
        a[i]=read();
    }
    for(int i=0;i<=m;i++){
        b[i]=read();
    }
    while(limit<=n+m){
        limit<<=1;
        L++;
    }
    for(int i=0;i<limit;i++){
        r[i]=(r[i>>1]>>1)|((i&1)<<(L-1));
    }
    NTT(a,1);
    NTT(b,1);
    for(int i=0;i<limit;i++){
        c[i]=(a[i]*b[i])%p;
    }
    NTT(c,-1);
    for(int i=0;i<=n+m;i++){
        printf("%lld ",c[i]);
    }
}

5.其他：

　　约瑟夫问题： 假设编号从0开始   F(i)表示在有i个人参与下 报数为m时 最后获胜的玩家编号 f[1]=0 ，f[i]=(f[i-1]+m) % i ，(i>1）

　　　　　　　　 报数为2时 J(g)表示g个人参与下最终获胜的人的编号   设g=2**t+x (2t>x 且 x≥0) 则 J(g)=2x+1​     2**t为不超过g的最大的二次幂

　　　　　　　　一些约瑟夫问题的好题：罗德岛裁员