外微分 全微分 极限 连续 可导 可微

 

如果函数z = f (x, y)在点(x,y)的全增量

 可表示为

其中A 、B仅与x、y 有关，而不依赖于Δx 、Δy，

 ，则称函数z = f (x, y)在点(x,y)处可微分， AΔx+BΔy称为函数z = f (x, y)在点(x,y)处的全微分。记作dz，即

。

函数若在某平面区域D内处处可微时，则称这个函数是D内的可微函数，全微分的定义可推广到三元及三元以上函数。

 

定理1

如果函数z=f（x，y）在点p0（x0，y0）处可微，则z=f（x，y）在p0（x0，y0）处连续，且各个偏导数存在，并且有f′x（x0，y0）=A，f′y（x0，y0）=B。

定理2

若函数z=f（x，y）在点p0（x0，y0）处的偏导数f′x，f′y连续，则函数f在点p0处可微。

定理3

若函数z = f (x, y)在点(x, y)可微分，则该函数在点(x,y)的偏导数

必存在，且函数z = f (x, y)在点(x,y)的全微分为：

 

判别可微方法

 

1.若f (x,y)在点(x0, y0)不连续，或偏导不存在，则必不可微；

2.若f (x,y)在点(x0, y0)的邻域内偏导存在且连续必可微；

3.检查

是否为

的高阶无穷小，若是则可微，否则不可微。

 

 

 

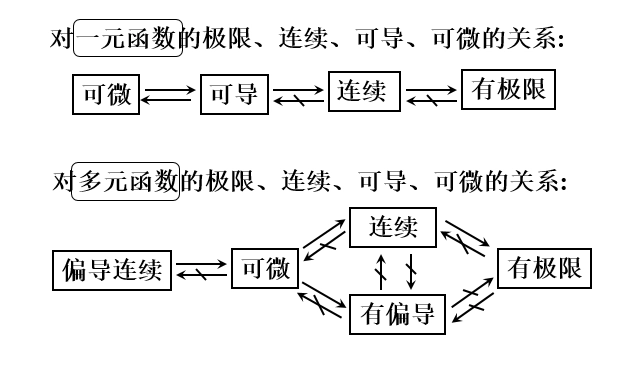
外微分_百度百科 https://baike.baidu.com/item/%E5%A4%96%E5%BE%AE%E5%88%86/1802695?fr=aladdin

 

The exterior derivative of a differential form of degree k is a differential form of degree k + 1.

If  f  is a smooth function (a 0-form), then the exterior derivative of  f  is the differential of  f . That is, df  is the unique 1-form such that for every smooth vector field X, df (X) = d_X f , where d_X f  is the directional derivative of  f  in the direction of X.

There are a variety of equivalent definitions of the exterior derivative of a general k-form.

In terms of axioms

The exterior derivative is defined to be the unique ℝ-linear mapping from k-forms to (k + 1)-forms satisfying the following properties:

1. df  is the differential of  f  for smooth functions  f .
2. d(df ) = 0 for any smooth function  f .
3. d(α ∧ β) = dα ∧ β + (−1)^p (α ∧ dβ) where α is a p-form. That is to say, d is an antiderivation of degree 1 on the exterior algebra of differential forms.

The second defining property holds in more generality: in fact, d(dα) = 0 for any k-form α; more succinctly, d² = 0. The third defining property implies as a special case that if  f  is a function and α a k-form, then d( fα) = d( f ∧ α) = df  ∧ α +  f  ∧ dα because functions are 0-forms, and scalar multiplication and the exterior product are equivalent when one of the arguments is a scalar.

 

翻译

搜索

复制