Cauchy sequence Hilbert space 希尔波特空间的柯西序列
http://mathworld.wolfram.com/HilbertSpace.html
A Hilbert space is a vector space ![]() with an inner product
with an inner product ![]() such that the norm defined by
such that the norm defined by
turns ![]() into a complete metric space. If the metric defined by the norm is not complete, then
into a complete metric space. If the metric defined by the norm is not complete, then ![]() is instead known as an inner product space.
is instead known as an inner product space.
Examples of finite-dimensional Hilbert spaces include
1. The real numbers ![]() with
with ![]() the vector dot product of
the vector dot product of ![]() and
and ![]() .
.
2. The complex numbers ![]() with
with ![]() the vector dot product of
the vector dot product of ![]() and the complex conjugate of
and the complex conjugate of ![]() .
.
An example of an infinite-dimensional Hilbert space is ![]() , the set of all functions
, the set of all functions ![]() such that the integral of
such that the integral of ![]() over the whole real line is finite. In this case, the inner product is
over the whole real line is finite. In this case, the inner product is
A Hilbert space is always a Banach space, but the converse need not hold.
A (small) joke told in the hallways of MIT ran, "Do you know Hilbert? No? Then what are you doing in his space?" (S. A. Vaughn, pers. comm., Jul. 31, 2005).
http://www.gatsby.ucl.ac.uk/~gretton/coursefiles/lecture4_introToRKHS.pdf
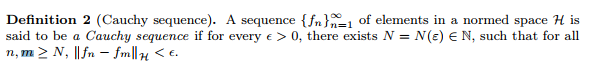
zh.wikipedia.org/wiki/希尔伯特空间
在数学里,希尔伯特空间即完备的内积空间,也就是说一个带有内积的完备向量空间。是有限维欧几里得空间的一个推广,使之不局限于实数的情形和有限的维数,但又不失完备性(而不像一般的非欧几里得空间那样破坏了完备性)。与欧几里得空间相仿,希尔伯特空间也是一个内积空间,其上有距离和角的概念(及由此引伸而来的正交性与垂直性的概念)。此外,希尔伯特空间还是一个完备的空间,其上所有的柯西序列会收敛到此空间里的一点,从而微积分中的大部分概念都可以无障碍地推广到希尔伯特空间中。希尔伯特空间为基于任意正交系上的多项式表示的傅立叶级数和傅立叶变换提供了一种有效的表述方式,而这也是泛函分析的核心概念之一。希尔伯特空间是公设化数学和量子力学的关键性概念之一。
en.wikipedia.org/wiki/Hilbert_space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions. A Hilbert space is an abstract vector space possessing the structure of an inner product that allows length and angle to be measured. Furthermore, Hilbert spaces are complete: there are enough limits in the space to allow the techniques of calculus to be used.
Hilbert spaces arise naturally and frequently in mathematics and physics, typically as infinite-dimensional function spaces. The earliest Hilbert spaces were studied from this point of view in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer)—and ergodic theory, which forms the mathematical underpinning of thermodynamics. John von Neumann coined the term Hilbert space for the abstract concept that underlies many of these diverse applications. The success of Hilbert space methods ushered in a very fruitful era for functional analysis. Apart from the classical Euclidean spaces, examples of Hilbert spaces include spaces of square-integrable functions, spaces of sequences, Sobolev spaces consisting of generalized functions, and Hardy spaces of holomorphic functions.



