函数的光滑化或正则化 卷积 应用 两个统计独立变量X与Y的和的概率密度函数是X与Y的概率密度函数的卷积
http://graphics.stanford.edu/courses/cs178/applets/convolution.html
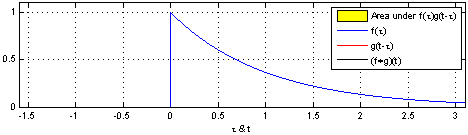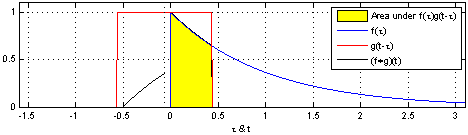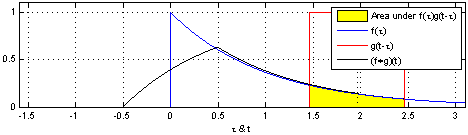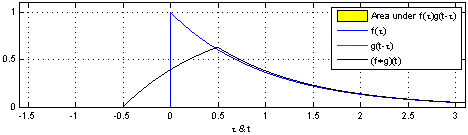
Convolution is an operation on two functions f and g, which produces a third function that can be interpreted as a modified ("filtered") version of f. In this interpretation we call g the filter. If f is defined on a spatial variable like x rather than a time variable like t, we call the operation spatial convolution. Convolution lies at the heart of any physical device or computational procedure that performs smoothing or sharpening. Applied to two dimensional functions like images, it's also useful for edge finding, feature detection, motion detection, image matching, and countless other tasks. Formally, for functions f(x) and g(x) of a continuous variable x, convolution is defined as: 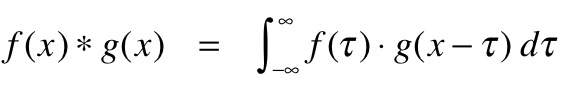
where * means convolution and · means ordinary multiplication. For functions of a discrete variable x, i.e. arrays of numbers, the definition is: 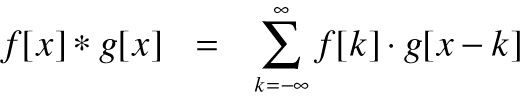
Finally, for functions of two variables x and y (for example images), these definitions become: 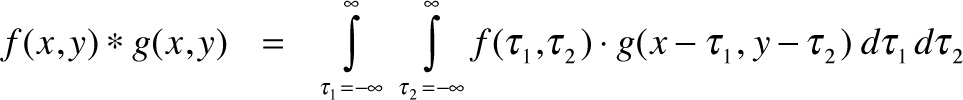
and 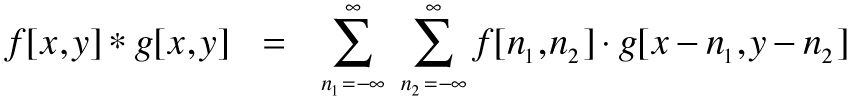
In digital photography, the image produced by the lens is a continuous function f(x,y), Placing an antialiasing filter in front of the sensor convolves this image by a smoothing filter g(x,y). This is the third equation above. Once the image has been recorded by a sensor and stored in a file, loading the file into Photoshop and sharpening it using a filter g[x,y] is the fourth equation.
zh.wikipedia.org/wiki/移動平均
移动平均(英语:moving average,MA),又称“移动平均线”简称均线,是技术分析中一种分析时间序列数据的工具。最常见的是利用股价、回报或交易量等变数计算出移动平均。
移动平均可抚平短期波动,反映出长期趋势或周期。数学上,移动平均可视为一种卷积。
zh.wikipedia.org/wiki/卷积
由卷积得到的函数








卷积的概念还可以推广到数列、测度以及广义函数上去。
卷积在科学、工程和数学上都有很多应用:
- 图像处理中,用作图像模糊、锐化、边缘检测。
- 统计学中,加权的滑动平均是一种卷积。
- 概率论中,两个统计独立变量X与Y的和的概率密度函数是X与Y的概率密度函数的卷积。
- 声学中,回声可以用源声与一个反映各种反射效应的函数的卷积表示。
- 电子工程与信号处理中,任一个线性系统的输出都可以通过将输入信号与系统函数(系统的冲激响应)做卷积获得。
- 物理学中,任何一个线性系统(符合叠加原理)都存在卷积。
https://en.wikipedia.org/wiki/Convolution





 浙公网安备 33010602011771号
浙公网安备 33010602011771号