B tree B+ tree B树 B+树 平衡多叉搜索树

 

 

B-tree - Wikipedia https://en.wikipedia.org/wiki/B-tree

B+ tree - Wikipedia https://en.wikipedia.org/wiki/B%2B_tree

 

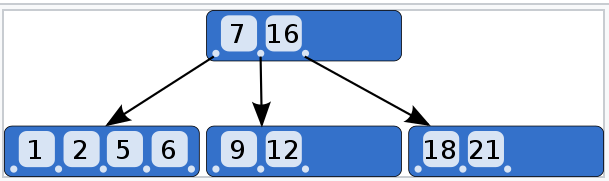
 A B-tree (Bayer & McCreight 1972) of order 5 (Knuth 1998).

 

 

 

 

 

 B tree  B+ tree B树 B+树 平衡多叉搜索树 

Difference between B tree and B+ tree - GeeksforGeeks https://www.geeksforgeeks.org/difference-between-b-tree-and-b-tree/

Basis of ComparisionB treeB+ tree
Pointers All internal and leaf nodes have data pointers Only leaf nodes have data pointers
Search Since all keys are not available at leaf, search often takes more time. All keys are at leaf nodes, hence search is faster and accurate..
Redundent Keys No duplicate of keys is maintained in the tree. Duplicate of keys are maintained and all nodes are present at leaf.
Insertion Insertion takes more time and it is not predictable sometimes. Insertion is easier and the results are always the same.
Deletion Deletion of internal node is very complex and tree has to undergo lot of transformations. Deletion of any node is easy because all node are found at leaf.
Leaf Nodes Leaf nodes are not stored as structural linked list. Leaf nodes are stored as structural linked list.
Access Sequential access to nodes is not possible Sequential access is possible just like linked list
Height For a particular number nodes height is larger Height is lesser than B tree for the same number of nodes
Application B-Trees used in Databases,Search engines B+ Trees used in Multilevel Indexing, Database indexing
Number of Nodes Number of nodes at any intermediary level ‘l’ is 2l. Each intermediary node can have n/2 to n children.

 

Introduction of B-Tree - GeeksforGeeks https://www.geeksforgeeks.org/introduction-of-b-tree-2/

Introduction: 
B-Tree is a self-balancing search tree. In most of the other self-balancing search trees (like AVL and Red-Black Trees), it is assumed that everything is in main memory. To understand the use of B-Trees, we must think of the huge amount of data that cannot fit in main memory. When the number of keys is high, the data is read from disk in the form of blocks. Disk access time is very high compared to the main memory access time. The main idea of using B-Trees is to reduce the number of disk accesses. Most of the tree operations (search, insert, delete, max, min, ..etc ) require O(h) disk accesses where h is the height of the tree. B-tree is a fat tree. The height of B-Trees is kept low by putting maximum possible keys in a B-Tree node. Generally, the B-Tree node size is kept equal to the disk block size. Since the height of the B-tree is low so total disk accesses for most of the operations are reduced significantly compared to balanced Binary Search Trees like AVL Tree, Red-Black Tree, ..etc.
Time Complexity of B-Tree: 
 

Sr. No.AlgorithmTime Complexity
1. Search O(log n)
2. Insert O(log n)
3. Delete O(log n)

“n” is the total number of elements in the B-tree.
Properties of B-Tree: 
 

    1. All leaves are at the same level.
    2. A B-Tree is defined by the term minimum degree ‘t’. The value of t depends upon disk block size.
    3. Every node except root must contain at least t-1 keys. The root may contain minimum 1 key.
    4. All nodes (including root) may contain at most 2*t – 1 keys.
    5. Number of children of a node is equal to the number of keys in it plus 1.
    6. All keys of a node are sorted in increasing order. The child between two keys k1 and k2 contains all keys in the range from k1 and k2.
    7. B-Tree grows and shrinks from the root which is unlike Binary Search Tree. Binary Search Trees grow downward and also shrink from downward.
    8. Like other balanced Binary Search Trees, time complexity to search, insert and delete is O(log n).
    9. Insertion of a Node in B-Tree happens only at Leaf Node.

Introduction of B+ Tree - GeeksforGeeks https://www.geeksforgeeks.org/introduction-of-b-tree/

 

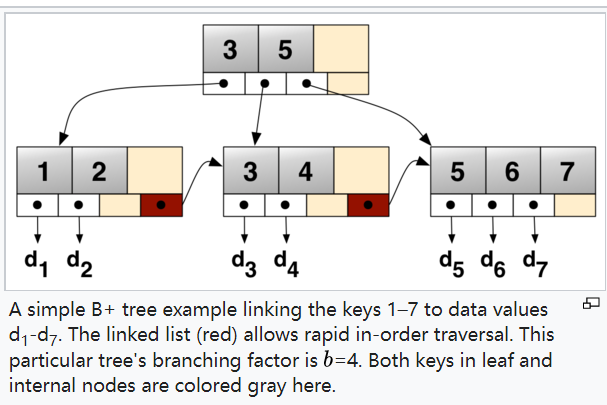
In order, to implement dynamic multilevel indexing, B-tree and B+ tree are generally employed. The drawback of the B-tree used for indexing, however, is that it stores the data pointer (a pointer to the disk file block containing the key value), corresponding to a particular key value, along with that key value in the node of a B-tree. This technique, greatly reduces the number of entries that can be packed into a node of a B-tree, thereby contributing to the increase in the number of levels in the B-tree, hence increasing the search time of a record. B+ tree eliminates the above drawback by storing data pointers only at the leaf nodes of the tree. Thus, the structure of leaf nodes of a B+ tree is quite different from the structure of internal nodes of the B tree. It may be noted here that, since data pointers are present only at the leaf nodes, the leaf nodes must necessarily store all the key values along with their corresponding data pointers to the disk file block, in order to access them. Moreover, the leaf nodes are linked to providing ordered access to the records. The leaf nodes, therefore form the first level of the index, with the internal nodes forming the other levels of a multilevel index. Some of the key values of the leaf nodes also appear in the internal nodes, to simply act as a medium to control the searching of a record. From the above discussion, it is apparent that a B+ tree, unlike a B-tree has two orders, ‘a’ and ‘b’, one for the internal nodes and the other for the external (or leaf) nodes. The structure of the internal nodes of a B+ tree of order ‘a’ is as follows:

  1. Each internal node is of the form: <P1, K1, P2, K2, ….., Pc-1, Kc-1, Pc> where c <= a and each Pi is a tree pointer (i.e points to another node of the tree) and, each Ki is a key-value (see diagram-I for reference).
  2. Every internal node has : K1 < K2 < …. < Kc-1
  3. For each search field values ‘X’ in the sub-tree pointed at by Pi, the following condition holds : Ki-1 < X <= Ki, for 1 < i < c and, Ki-1 < X, for i = c (See diagram I for reference)
  4. Each internal node has at most ‘a’ tree pointers.
  5. The root node has, at least two tree pointers, while the other internal nodes have at least \ceil(a/2) tree pointers each.
  6. If an internal node has ‘c’ pointers, c <= a, then it has ‘c – 1’ key values.

 Diagram-I The structure of the leaf nodes of a B+ tree of order ‘b’ is as follows:

  1. Each leaf node is of the form: <<K1, D1>, <K2, D2>, ….., <Kc-1, Dc-1>, Pnext> where c <= b and each Di is a data pointer (i.e points to actual record in the disk whose key value is Ki or to a disk file block containing that record) and, each Ki is a key value and, Pnext points to next leaf node in the B+ tree (see diagram II for reference).
  2. Every leaf node has : K1 < K2 < …. < Kc-1, c <= b
  3. Each leaf node has at least \ceil(b/2) values.
  4. All leaf nodes are at the same level.

 Diagram-II Using the Pnext pointer it is viable to traverse all the leaf nodes, just like a linked list, thereby achieving ordered access to the records stored in the disk. A Diagram of B+ Tree – 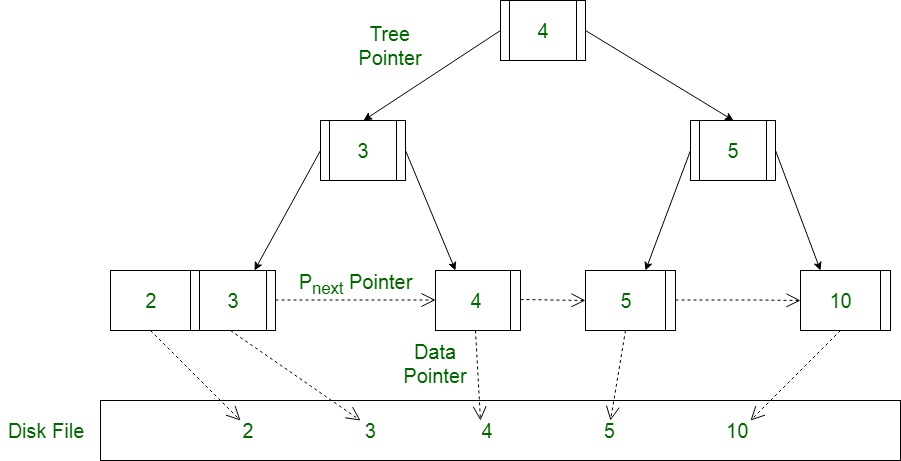 Advantage – A B+ tree with ‘l’ levels can store more entries in its internal nodes compared to a B-tree having the same ‘l’ levels. This accentuates the significant improvement made to the search time for any given key. Having lesser levels and the presence of Pnext pointers imply that the B+ trees is very quick and efficient in accessing records from disks.

Application of B+ Trees:

  • Multilevel Indexing
  • Faster operations on the tree (insertion, deletion, search)
  • Database indexing

 

 

 

 

posted @ 2017-07-02 15:15  papering  阅读(294)  评论(0)  编辑  收藏  举报