AVL 左旋 右旋 左左 左右 右左 右右
Data Structures and Algorithms: Red-Black Trees https://www.cs.auckland.ac.nz/software/AlgAnim/red_black.html

A rotation is a local operation in a search tree that preserves in-order traversal key ordering.
Note that in both trees, an in-order traversal yields:
A x B y C
旋转前后,中序遍历的结果不变。
AVL Tree | Set 1 (Insertion) - GeeksforGeeks https://www.geeksforgeeks.org/avl-tree-set-1-insertion/
AVL Tree | Set 2 (Deletion) - GeeksforGeeks https://www.geeksforgeeks.org/avl-tree-set-2-deletion/
Insertion
To make sure that the given tree remains AVL after every insertion, we must augment the standard BST insert operation to perform some re-balancing. Following are two basic operations that can be performed to re-balance a BST without violating the BST property (keys(left) < key(root) < keys(right)).
- Left Rotation
- Right Rotation
T1, T2 and T3 are subtrees of the tree
rooted with y (on the left side) or x (on
the right side)
y x
/ \ Right Rotation / \
x T3 - - - - - - - > T1 y
/ \ < - - - - - - - / \
T1 T2 Left Rotation T2 T3
Keys in both of the above trees follow the
following order
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere.
Steps to follow for insertion
Let the newly inserted node be w
- Perform standard BST insert for w.
- Starting from w, travel up and find the first unbalanced node. Let z be the first unbalanced node, y be the child of z that comes on the path from w to z and x be the grandchild of z that comes on the path from w to z.
- Re-balance the tree by performing appropriate rotations on the subtree rooted with z. There can be 4 possible cases that needs to be handled as x, y and z can be arranged in 4 ways. Following are the possible 4 arrangements:
- y is left child of z and x is left child of y (Left Left Case)
- y is left child of z and x is right child of y (Left Right Case)
- y is right child of z and x is right child of y (Right Right Case)
- y is right child of z and x is left child of y (Right Left Case)
Following are the operations to be performed in above mentioned 4 cases. In all of the cases, we only need to re-balance the subtree rooted with z and the complete tree becomes balanced as the height of subtree (After appropriate rotations) rooted with z becomes same as it was before insertion. (See this video lecture for proof)
a) Left Left Case
T1, T2, T3 and T4 are subtrees.
z y
/ \ / \
y T4 Right Rotate (z) x z
/ \ - - - - - - - - -> / \ / \
x T3 T1 T2 T3 T4
/ \
T1 T2
b) Left Right Case
z z x
/ \ / \ / \
y T4 Left Rotate (y) x T4 Right Rotate(z) y z
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
T1 x y T3 T1 T2 T3 T4
/ \ / \
T2 T3 T1 T2
c) Right Right Case
z y
/ \ / \
T1 y Left Rotate(z) z x
/ \ - - - - - - - -> / \ / \
T2 x T1 T2 T3 T4
/ \
T3 T4
d) Right Left Case
z z x
/ \ / \ / \
T1 y Right Rotate (y) T1 x Left Rotate(z) z y
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
x T4 T2 y T1 T2 T3 T4
/ \ / \
T2 T3 T3 T4
Insertion Examples:
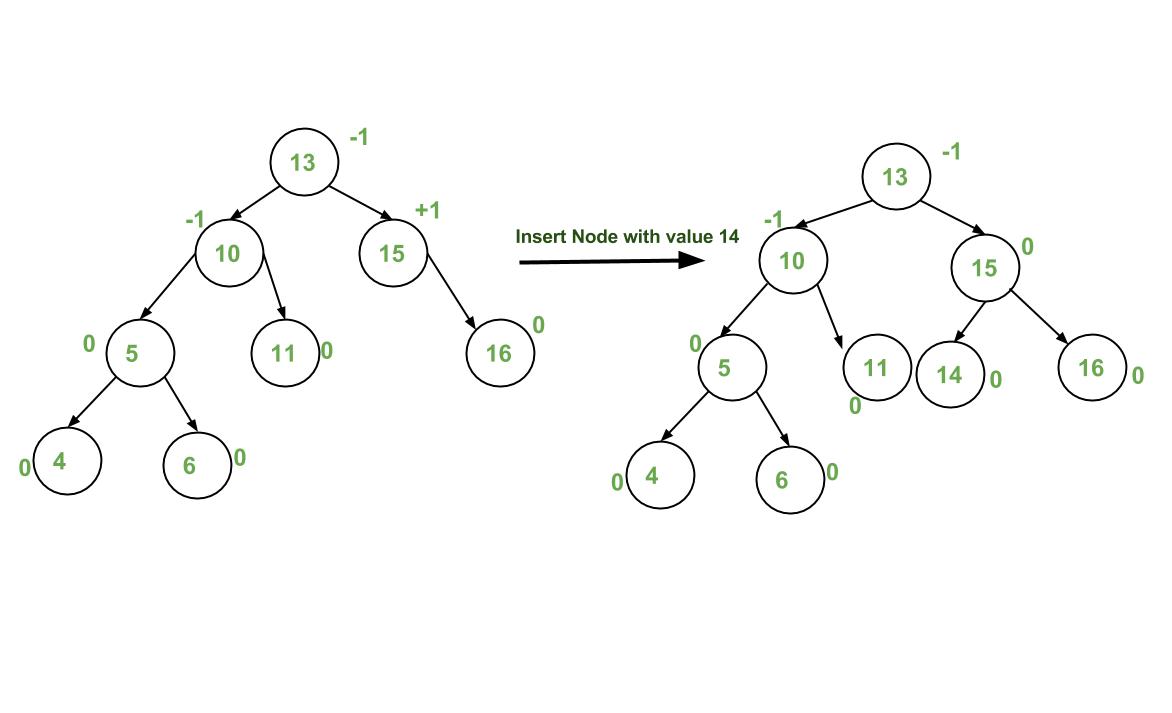
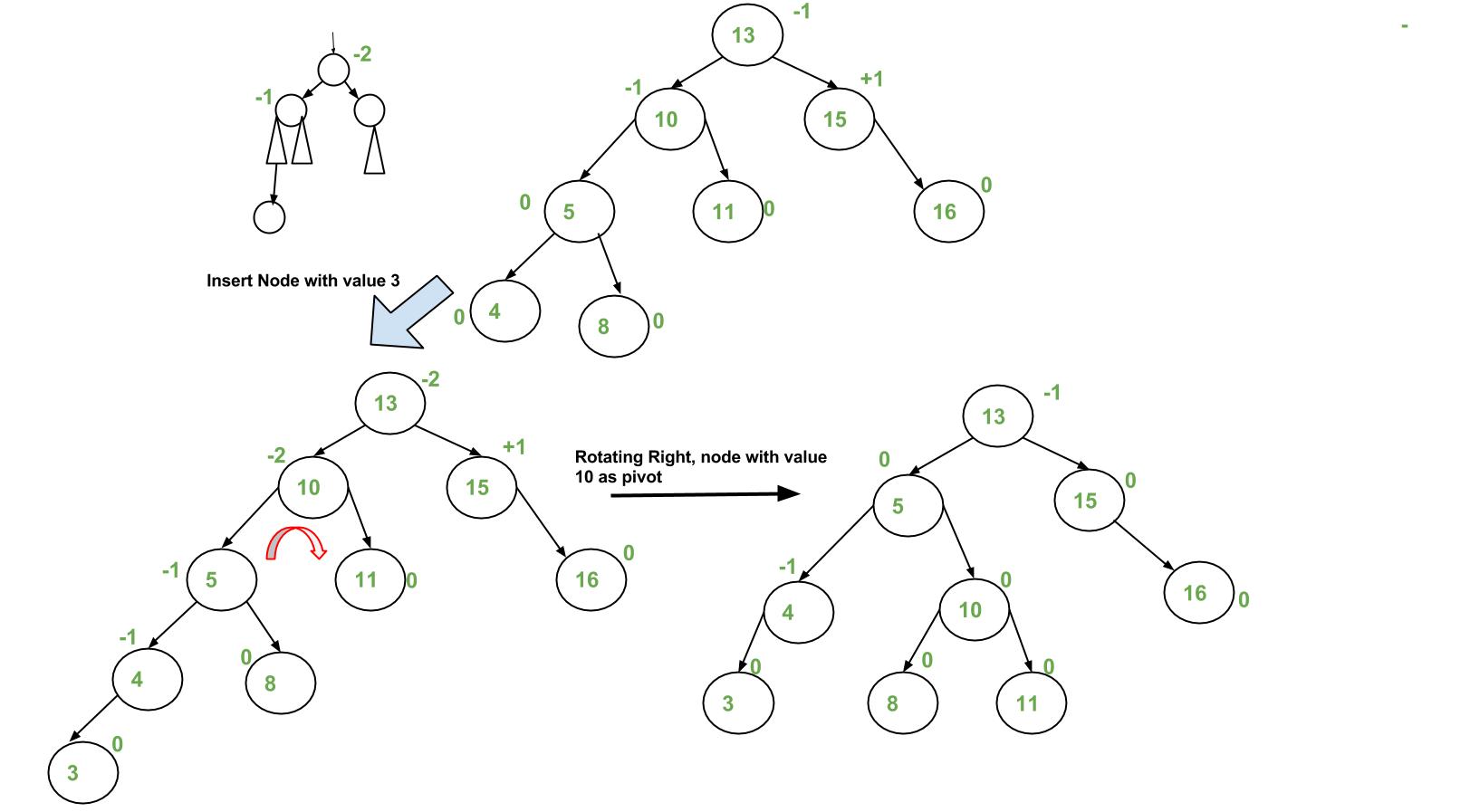
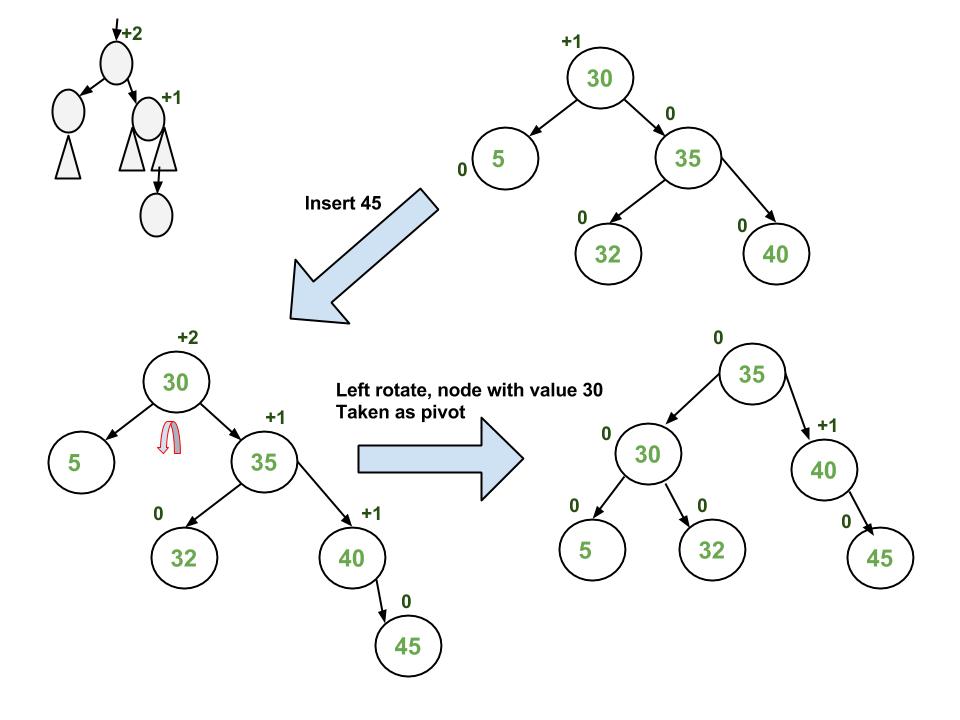
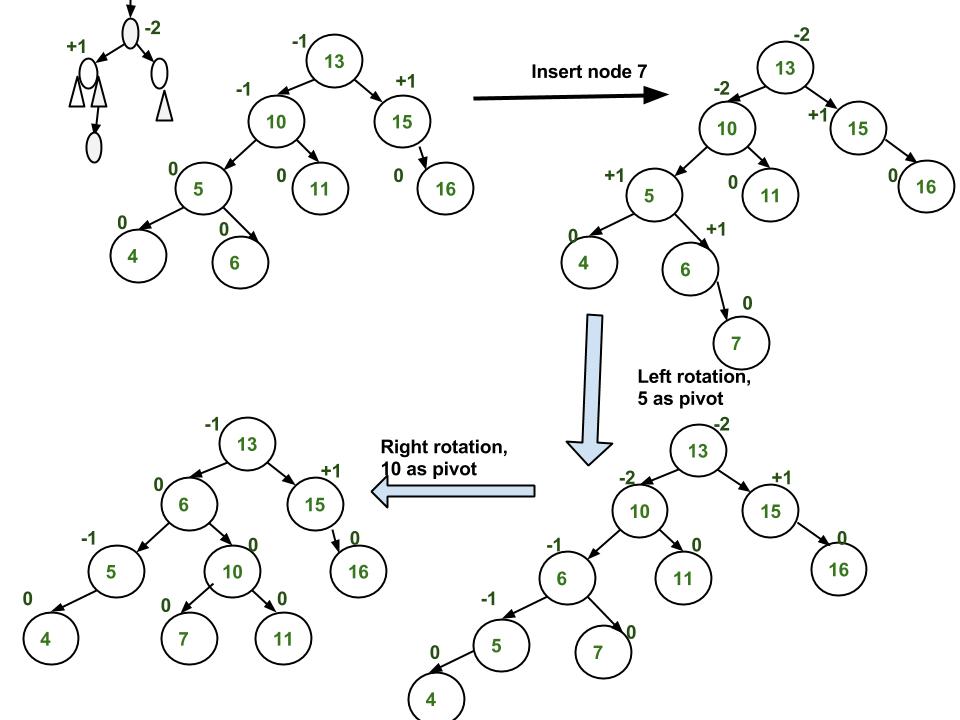
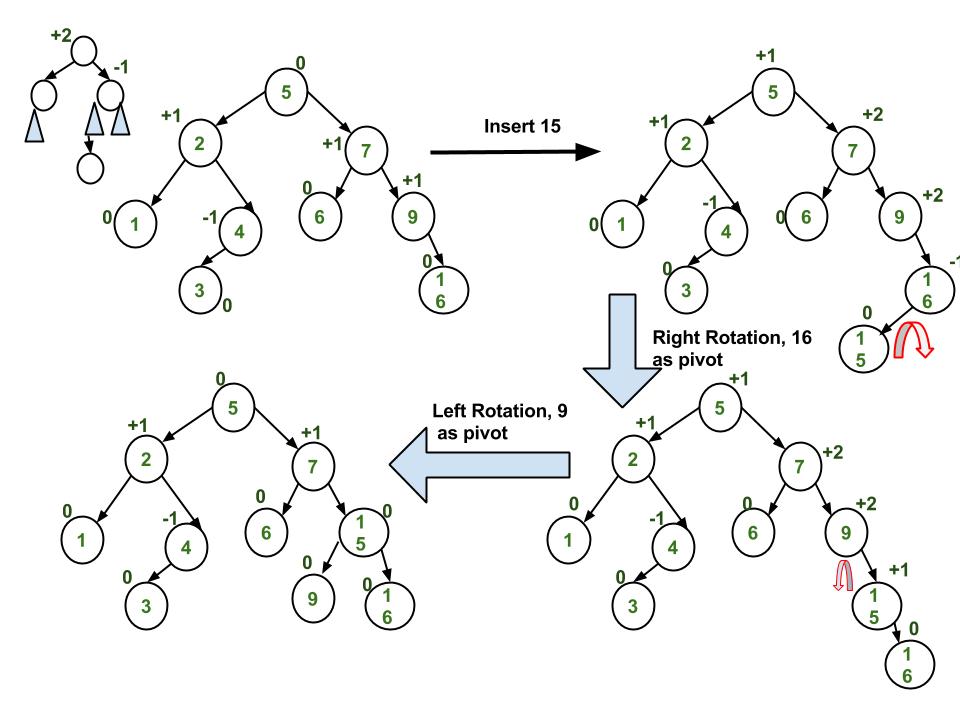
Implementation:
Following is the implementation for AVL Tree Insertion. The following implementation uses the recursive BST insert to insert a new node. In the recursive BST insert, after insertion, we get pointers to all ancestors one by one in a bottom-up manner. So we don’t need parent pointer to travel up. The recursive code itself travels up and visits all the ancestors of the newly inserted node.
- Perform the normal BST insertion.
- The current node must be one of the ancestors of the newly inserted node. Update the height of the current node.
- Get the balance factor (left subtree height – right subtree height) of the current node.
- If balance factor is greater than 1, then the current node is unbalanced and we are either in Left Left case or left Right case. To check whether it is left left case or not, compare the newly inserted key with the key in left subtree root.
- If balance factor is less than -1, then the current node is unbalanced and we are either in Right Right case or Right-Left case. To check whether it is Right Right case or not, compare the newly inserted key with the key in right subtree root.
package avl
// An AVL tree node
type Node struct {
Key int
Left *Node
Right *Node
Height int
}
// Helper function that allocates a new node with the given key and NULL left and right pointers.
func NewNode(key int) *Node {
i := &Node{}
i.Key = key
return i
}
// A utility function to get maximum of two integers
func max(a, b int) int {
if a > b {
return a
}
return b
}
// A utility function to get the height of the tree
func height(n *Node) int {
if n == nil {
return 0
}
return 1 + max(height(n.Left), height(n.Right))
}
/*
T1, T2 and T3 are subtrees of the tree
rooted with y (on the left side) or x (on
the right side)
y x
/ \ Right Rotation / \
x T3 - - - - - - - > T1 y
/ \ < - - - - - - - / \
T1 T2 Left Rotation T2 T3
Keys in both of the above trees follow the
following order
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere.
*/
// 旋转,改变了父子关系
// A utility function to right rotate subtree rooted with y
// See the diagram given above.
func rightRotate(y *Node) *Node {
x := y.Left
T2 := x.Right
// Perform rotation
x.Right = y
y.Left = T2
// Update heights
// 注意:先子后父
y.Height = height(y)
x.Height = height(x)
// Return new root
return x
}
func leftRotate(x *Node) *Node {
y := x.Right
T2 := y.Left
y.Left = x
x.Right = T2
x.Height = height(x)
y.Height = height(y)
return y
}
// 左子树高度-右子树的高度差
// Get Balance factor of node N
func getBalance(n *Node) int {
if n == nil {
return 0
}
return height(n.Left) - height(n.Right)
}
// Recursive function to insert a key in the subtree rooted
// with node and returns the new root of the subtree.
func Insert(n *Node, key int) *Node {
/* 1. Perform the normal BST insertion */
if n == nil {
return NewNode(key)
}
if key < n.Key {
n.Left = Insert(n.Left, key)
} else if key > n.Key {
n.Right = Insert(n.Right, key)
} else {
// Equal keys are not allowed in BST
return n
}
/* 2. Update height of this ancestor node */
n.Height = height(n)
/* 3. Get the balance factor of this ancestor
node to check whether this node became
unbalanced */
balance := getBalance(n)
// If this node becomes unbalanced, then
// there are 4 cases
// Left Left Case
if balance > 1 && key < n.Left.Key {
return rightRotate(n)
}
// Right Right Case
if balance < -1 && key > n.Right.Key {
return leftRotate(n)
}
// Left Right Case
if balance > 1 && key > n.Left.Key {
n.Left = leftRotate(n.Left)
return rightRotate(n)
}
// Right Left Case
if balance < -1 && key < n.Right.Key {
n.Right = rightRotate(n.Right)
return leftRotate(n)
}
/* return the (unchanged) node pointer */
return n
}
/* Given a non-empty binary search tree, return the
node with minimum key value found in that tree.
Note that the entire tree does not need to be
searched. */
func minValNode(n *Node) *Node {
current := n
/* loop down to find the leftmost leaf */
for current.Left != nil {
current = current.Left
}
return current
}
func deleteNode(root *Node, key int) *Node {
// STEP 1: PERFORM STANDARD BST DELETE
if root == nil {
return nil
}
if key < root.Key {
// If the key to be deleted is smaller than the
// root's key, then it lies in left subtree
root.Left = deleteNode(root.Left, key)
} else if key > root.Key {
// If the key to be deleted is greater than the
// root's key, then it lies in right subtree
root.Right = deleteNode(root.Right, key)
} else {
// if key is same as root's key, then This is
// the node to be deleted
// node with only one child or no child
if root.Left == nil || root.Right == nil {
// No child case
if root.Left == nil && root.Right == nil {
root = nil
} else {
// One child case
var temp *Node
if root.Left != nil {
temp = root.Left
} else {
temp = root.Right
}
// Copy the contents of the non-empty child
root = temp
}
} else {
// node with two children: Get the inorder
// successor (smallest in the right subtree)
var temp *Node
temp = minValNode(root.Right)
// Copy the inorder successor's data to this node
root.Key = temp.Key
// Delete the inorder successor
root.Right = deleteNode(root.Right, temp.Key)
}
}
// If the tree had only one node then return
if root == nil {
return nil
}
// STEP 2: UPDATE HEIGHT OF THE CURRENT NODE
root.Height = 1 + max(height(root.Left), height(root.Right))
// STEP 3: GET THE BALANCE FACTOR OF THIS NODE (to
// check whether this node became unbalanced)
balance := getBalance(root)
// If this node becomes unbalanced, then there are 4 cases
// Left Left Case
if balance > 1 && getBalance(root.Left) >= 0 {
return rightRotate(root)
}
// Left Right Case
if balance > 1 && getBalance(root.Left) < 0 {
root.Left = leftRotate(root.Left)
return rightRotate(root)
}
// Right Right Case
if balance < -1 && getBalance(root.Right) <= 0 {
return leftRotate(root)
}
// Right Left Case
if balance < -1 && getBalance(root.Right) > 0 {
root.Right = rightRotate(root.Right)
return leftRotate(root)
}
return root
}
Time Complexity: The rotation operations (left and right rotate) take constant time as only few pointers are being changed there. Updating the height and getting the balance factor also take constant time. So the time complexity of AVL delete remains same as BST delete which is O(h) where h is height of the tree. Since AVL tree is balanced, the height is O(Logn). So time complexity of AVL delete is O(Log n).
Advantages Of AVL Trees
- It is always height balanced
- Height Never Goes Beyond LogN, where N is the number of nodes
- It give better search than compared to binary search tree
- It has self balancing capabilities
Summary of AVL Trees
- These are self-balancing binary search trees.
- Balancing Factor ranges -1, 0, and +1.
- When balancing factor goes beyond the range require rotations to be performed
- Insert, delete, and search time is O(log N).
- AVL tree are mostly used where search is more frequent compared to insert and delete operation.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号