Red Black Tree 红黑树 BST AVL trees 2-3 trees 2-3-4 trees B-trees Red-black trees Balanced search tree 平衡搜索树 左旋 右旋 二叉搜索树 平衡二叉树 AVL 哈希表


https://www.cs.usfca.edu/~galles/visualization/AlgorithmLibrary/RedBlack.js
红黑树的叶子节点: sentinel nodes 哨兵节点
平衡二叉搜索树的高度 保证了搜索的时间复杂度为 O(logN)
Data Structures and Algorithms: Red-Black Trees https://www.cs.auckland.ac.nz/software/AlgAnim/red_black_op.html
| Data Structures and Algorithms |
| 8.2 Red-Black Tree Operation |
Here's an example of insertion into a red-black tree (taken from Cormen, p269).
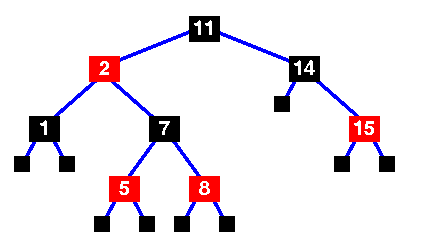 |
Here's the original tree .. Note that in the following diagrams, the black sentinel nodes have been omitted to keep the diagrams simple. |
 |
The tree insert routine has just been called to insert node "4" into the tree.
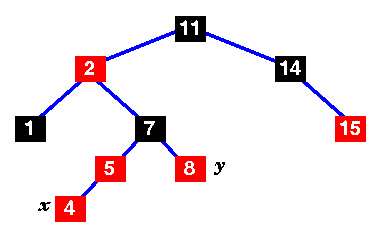
This is no longer a red-black tree - there are two successive red nodes on the path Mark the new node, x, and it's uncle, y. y is red, so we have case 1 ... |
 |
Change the colours of nodes 5, 7 and 8. |
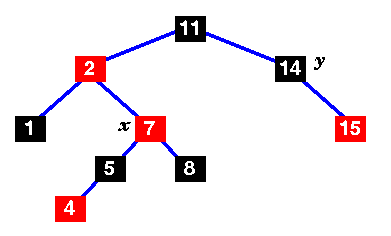 |
Move x up to its grandparent, 7.
x's parent (2) is still red, so this isn't a red-black tree yet. Mark the uncle, y. In this case, the uncle is black, so we have case 2 ... |
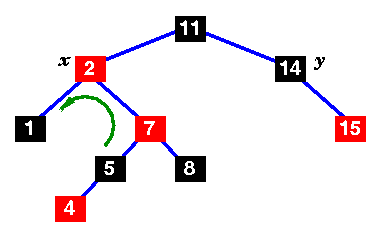 |
Move x up and rotate left. |
 |
Still not a red-black tree .. the uncle is black, but x's parent is to the left .. |
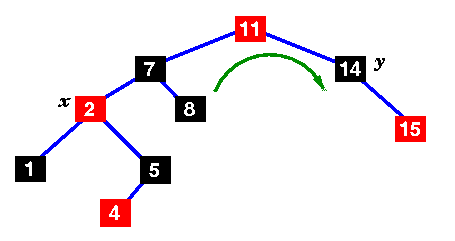 |
Change the colours of 7 and 11 and rotate right .. |
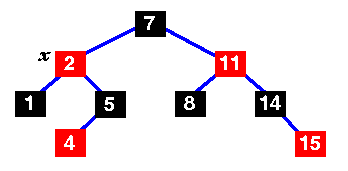 |
This is now a red-black tree, so we're finished!
O(logn) time! |
| Back to Red Black Trees | Back to the Table of Contents |
©  , 1998
, 1998
Data Structures and Algorithms: Red-Black Trees https://www.cs.auckland.ac.nz/software/AlgAnim/red_black.html
| Data Structures and Algorithms |
| 8.2 Red-Black Trees |
A red-black tree is a binary search tree with one extra attribute for each node: the colour, which is either red or black. We also need to keep track of the parent of each node, so that a red-black tree's node structure would be:
struct t_red_black_node {
enum { red, black } colour;
void *item;
struct t_red_black_node *left,
*right,
*parent;
}
For the purpose of this discussion, the NULL nodes which terminate the tree are considered to be the leaves and are coloured black.
Definition of a red-black tree
A red-black tree is a binary search tree which has the following red-black properties:
|
|
 |
A basic red-black tree |
 |
Basic red-black tree with the sentinel nodes added. Implementations of the red-black tree algorithms will usually include the sentinel nodes as a convenient means of flagging that you have reached a leaf node.
They are the NULL black nodes of property 2. |
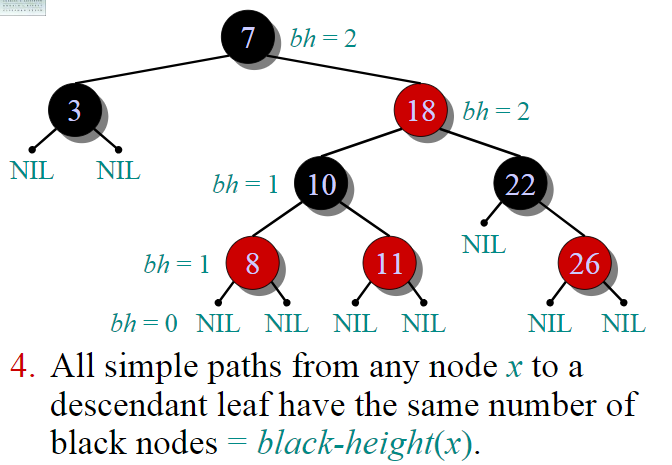
The number of black nodes on any path from, but not including, a node x to a leaf is called the black-height of a node, denoted bh(x). We can prove the following lemma:
Lemma
A red-black tree with n internal nodes has height at most 2log(n+1).
(For a proof, see Cormen, p 264)
This demonstrates why the red-black tree is a good search tree: it can always be searched in O(log n) time.
As with heaps, additions and deletions from red-black trees destroy the red-black property, so we need to restore it. To do this we need to look at some operations on red-black trees.
Rotations
| A rotation is a local operation in a search tree that preserves in-order traversal key ordering.
Note that in both trees, an in-order traversal yields:
A x B y C |
 |
The left_rotate operation may be encoded:
left_rotate( Tree T, node x ) {
node y;
y = x->right;
/* Turn y's left sub-tree into x's right sub-tree */
x->right = y->left;
if ( y->left != NULL )
y->left->parent = x;
/* y's new parent was x's parent */
y->parent = x->parent;
/* Set the parent to point to y instead of x */
/* First see whether we're at the root */
if ( x->parent == NULL ) T->root = y;
else
if ( x == (x->parent)->left )
/* x was on the left of its parent */
x->parent->left = y;
else
/* x must have been on the right */
x->parent->right = y;
/* Finally, put x on y's left */
y->left = x;
x->parent = y;
}
Insertion
Insertion is somewhat complex and involves a number of cases. Note that we start by inserting the new node, x, in the tree just as we would for any other binary tree, using the tree_insert function. This new node is labelled red, and possibly destroys the red-black property. The main loop moves up the tree, restoring the red-black property.
rb_insert( Tree T, node x ) {
/* Insert in the tree in the usual way */
tree_insert( T, x );
/* Now restore the red-black property */
x->colour = red;
while ( (x != T->root) && (x->parent->colour == red) ) {
if ( x->parent == x->parent->parent->left ) {
/* If x's parent is a left, y is x's right 'uncle' */
y = x->parent->parent->right;
if ( y->colour == red ) {
/* case 1 - change the colours */
x->parent->colour = black;
y->colour = black;
x->parent->parent->colour = red;
/* Move x up the tree */
x = x->parent->parent;
}
else {
/* y is a black node */
if ( x == x->parent->right ) {
/* and x is to the right */
/* case 2 - move x up and rotate */
x = x->parent;
left_rotate( T, x );
}
/* case 3 */
x->parent->colour = black;
x->parent->parent->colour = red;
right_rotate( T, x->parent->parent );
}
}
else {
/* repeat the "if" part with right and left
exchanged */
}
}
/* Colour the root black */
T->root->colour = black;
}
Here's an example of the insertion operation.
Animation
| Red-Black Tree Animation This animation was written by Linda Luo, Mervyn Ng, Anita Lee, John Morris and Woi Ang. |
|
Please email comments to: |
Examination of the code reveals only one loop. In that loop, the node at the root of the sub-tree whose red-black property we are trying to restore, x, may be moved up the tree at least one level in each iteration of the loop. Since the tree originally has O(log n) height, there are O(log n) iterations. The tree_insert routine also has O(log n) complexity, so overall the rb_insert routine also has O(log n) complexity.
Key terms |
- Red-black trees
- Trees which remain balanced - and thus guarantee O(logn) search times - in a dynamic environment. Or more importantly, since any tree can be re-balanced - but at considerable cost - can be re-balanced in O(logn) time.
| Continue on to AVL Trees | Back to the Table of Contents |
©  , 1998
, 1998
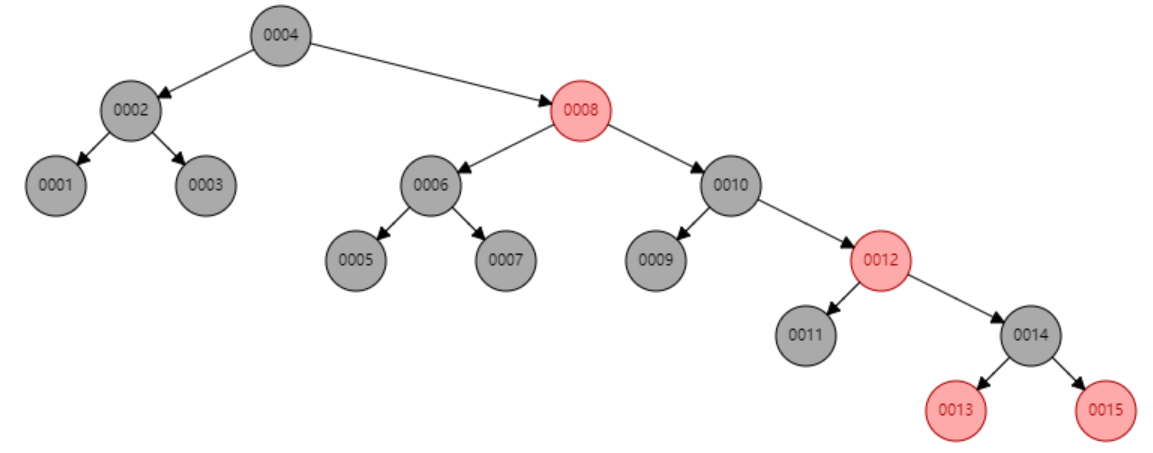
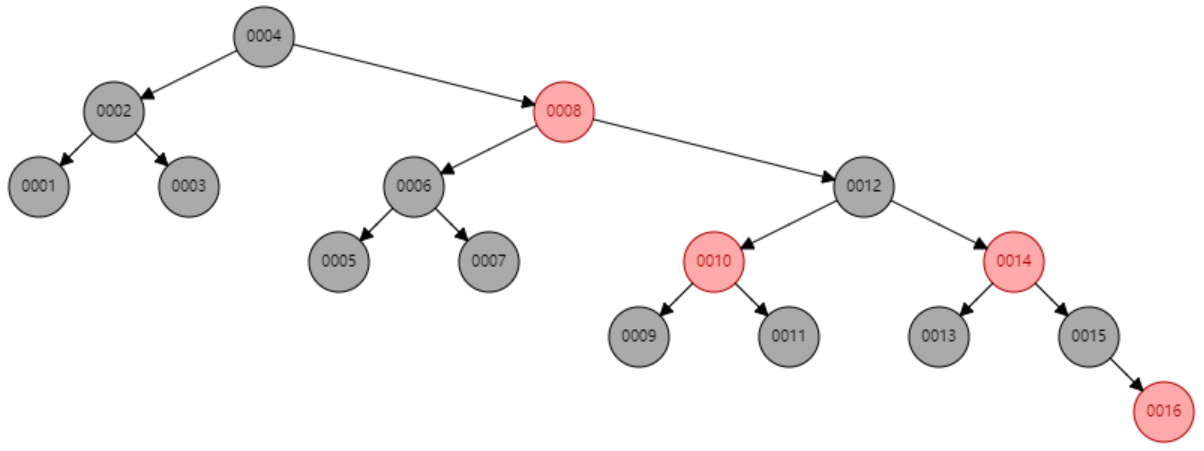
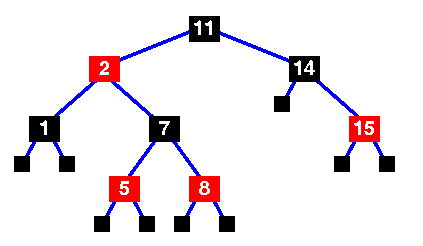
Example: Searching 11 in the following red-black tree.
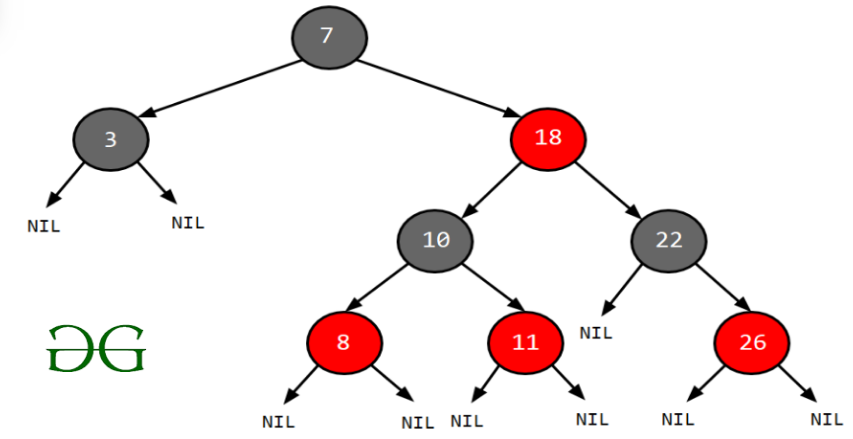
Solution:
- Start from the root.
- Compare the inserting element with root, if less than root, then recurse for left, else recurse for right.
- If the element to search is found anywhere, return true, else return false.
Red-Black Tree | Set 1 (Introduction) - GeeksforGeeks https://www.geeksforgeeks.org/red-black-tree-set-1-introduction-2/
Rules That Every Red-Black Tree Follows:
- Every node has a color either red or black.
- The root of the tree is always black.
- There are no two adjacent red nodes (A red node cannot have a red parent or red child).
- Every path from a node (including root) to any of its descendants NULL nodes has the same number of black nodes.
- All leaf nodes are black nodes.

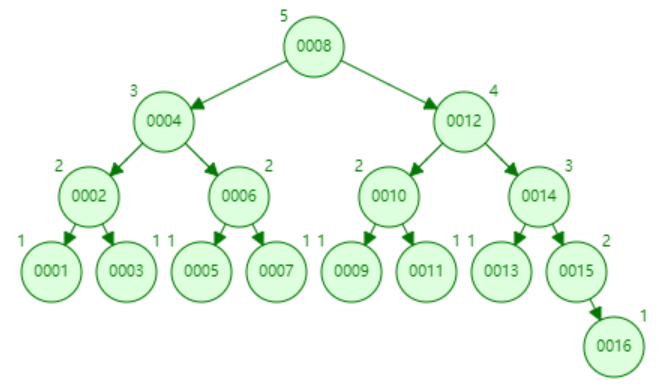
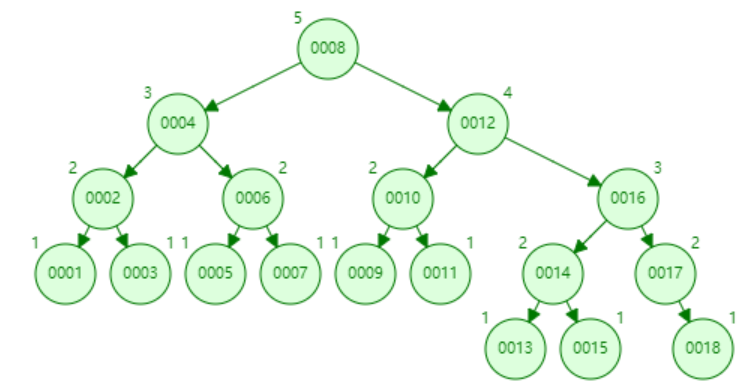
红黑树的左右子树高度差可能为2,故不是AVL树。

AVL 可视化 AVL Tree Visualzation https://www.cs.usfca.edu/~galles/visualization/AVLtree.html

AVL Tree | Set 1 (Insertion) - GeeksforGeeks https://www.geeksforgeeks.org/avl-tree-set-1-insertion/
BST的时间复杂度退化为O(n)
怎样转化为平衡
http://www.cse.chalmers.se/edu/year/2018/course/DAT037/slides/
Parent Directory -
[ ] 1.pdf 16-May-2019 18:34 3.0M
[ ] 2.pdf 16-May-2019 18:34 312K
[ ] 3.pdf 16-May-2019 18:34 253K
[ ] 4.pdf 16-May-2019 18:34 305K
[ ] 5.pdf 16-May-2019 18:34 294K
[ ] 6a-leftist-heaps.pdf 16-May-2019 18:34 107K
[ ] 6b-binary-search-tre..> 16-May-2019 18:34 353K
[ ] 6c-avl-trees.pdf 16-May-2019 18:34 313K
[ ] 7a-more-trees.pdf 16-May-2019 18:34 243K
[ ] 7b-tree-traversals.pdf 16-May-2019 18:34 83K
[ ] 7c-real-world-sortin..> 16-May-2019 18:34 92K
[ ] 8-graphs.pdf 16-May-2019 18:34 784K
[ ] 9-more-graphs.pdf 16-May-2019 18:34 1.1M
[ ] 10-linked-lists.pdf 16-May-2019 18:34 211K
[ ] 11-hash-tables.pdf 16-May-2019 18:34 187K
[ ] 12-tries.pdf 16-May-2019 18:34 538K
[ ] 13.pdf 16-May-2019 18:34 184K
https://baike.baidu.com/item/平衡树/7641279
平衡树(Balance Tree,BT) 指的是,任意节点的子树的高度差都小于等于1。常见的符合平衡树的有,B树(多路平衡搜索树)、AVL树(二叉平衡搜索树)等。平衡树可以完成集合的一系列操作, 时间复杂度和空间复杂度相对于“2-3树”要低,在完成集合的一系列操作中始终保持平衡,为大型数据库的组织、索引提供了一条新的途径。
https://leetcode.cn/problems/kth-smallest-element-in-a-bst/solution/er-cha-sou-suo-shu-zhong-di-kxiao-de-yua-8o07/
二叉搜索树 平衡二叉树 AVL
迭代 查找
https://leetcode-cn.com/problems/search-in-a-binary-search-tree/
func searchBST(root *TreeNode, val int) *TreeNode {
for root != nil {
if val == root.Val {
return root
}
if val < root.Val {
root = root.Left
} else {
root = root.Right
}
}
return nil
}
递归 查找
迭代 插入
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func insertIntoBST(root *TreeNode, val int) *TreeNode {
if root == nil {
return &TreeNode{Val: val}
}
p := root
for p != nil {
if val < p.Val {
if p.Left == nil {
p.Left = &TreeNode{Val: val}
break
}
p = p.Left
} else {
if p.Right == nil {
p.Right = &TreeNode{Val: val}
break
}
p = p.Right
}
}
return root
}
https://leetcode-cn.com/problems/insert-into-a-binary-search-tree/
Advantages of BST over Hash Table - GeeksforGeeks https://www.geeksforgeeks.org/advantages-of-bst-over-hash-table/
Hash Table supports following operations in Θ(1) time. 1) Search 2) Insert 3) Delete The time complexity of above operations in a self-balancing Binary Search Tree (BST) (like Red-Black Tree, AVL Tree, Splay Tree, etc) is O(Logn). So Hash Table seems to beating BST in all common operations. When should we prefer BST over Hash Tables, what are advantages. Following are some important points in favor of BSTs.
- We can get all keys in sorted order by just doing Inorder Traversal of BST. This is not a natural operation in Hash Tables and requires extra efforts.
- Doing order statistics, finding closest lower and greater elements, doing range queries are easy to do with BSTs. Like sorting, these operations are not a natural operation with Hash Tables.
- BSTs are easy to implement compared to hashing, we can easily implement our own customized BST. To implement Hashing, we generally rely on libraries provided by programming languages.
- With Self-Balancing BSTs, all operations are guaranteed to work in O(Logn) time. But with Hashing, Θ(1) is average time and some particular operations may be costly i.e, O(n2 ), especially when table resizing happens.
- In BST we can do range searches efficiently but in Hash Table we cannot do range search efficienly.
- BST are memory efficient but Hash table is not.
https://baike.baidu.com/item/红黑树/2413209
小结:
1、红黑树:典型的用途是实现关联数组
2、旋转
当我们在对红黑树进行插入和删除等操作时,对树做了修改,那么可能会违背红黑树的性质。
为了保持红黑树的性质,我们可以通过对树进行旋转,即修改树中某些结点的颜色及指针结构,以达到对红黑树进行插入、删除结点等操作时,红黑树依然能保持它特有的性质(五点性质)。
https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-046j-introduction-to-algorithms-sma-5503-fall-2005/video-lectures/lecture-10-red-black-trees-rotations-insertions-deletions/lec10.pdf
Balanced BSTs: the problem The BST operations take O(height of tree), so for unbalanced trees can take O(n) time
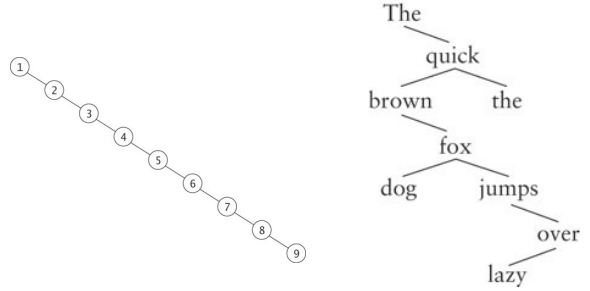
Balanced BSTs: the solution
Take BSTs and add an extra invariant that
makes sure that the tree is balanced
● Height of tree must be O(log n)
● Then all operations will take O(log n) time
One possible idea for an invariant:
● Height of left child = height of right child
(for all nodes in the tree)
● Tree would be sort of “perfectly balanced”
A too restrictive invariant
Perfect balance is too restrictive!
Number of nodes can only be 1, 3, 7, 15, 31, ...
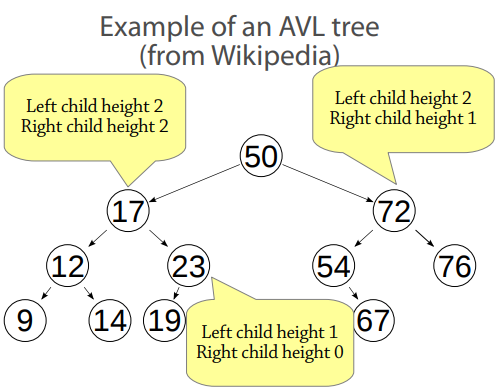
AVL trees – a less restrictive invariant
The AVL tree is the first balanced BST
discovered (from 1962) – it's named after
Adelson-Velsky and Landis
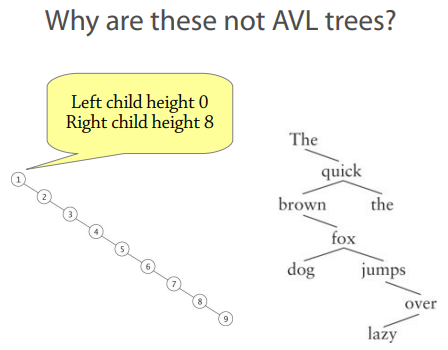
It's a BST with the following invariant:
● The difference in heights between the left and right
children of any node is at most 1
● (compared to 0 for a perfectly balanced tree)
This makes the tree's height O(log n), so it's
balanced

左旋、右旋 使不平衡的二叉搜索树平衡
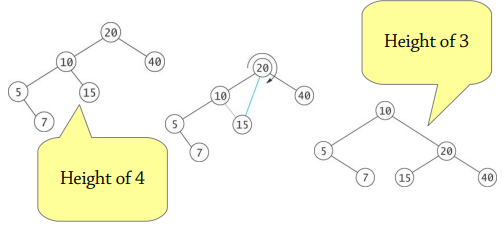
Rotation Rotation rearranges a BST by moving a different node to the root, without changing the BST's contents

We can strategically use rotations to rebalance an unbalanced tree. This is what most balanced BST variants do!
Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when implementing a dynamic set of n items.
AVL trees
2-3 trees
2-3-4 trees
B-trees
Red-black trees
【1】
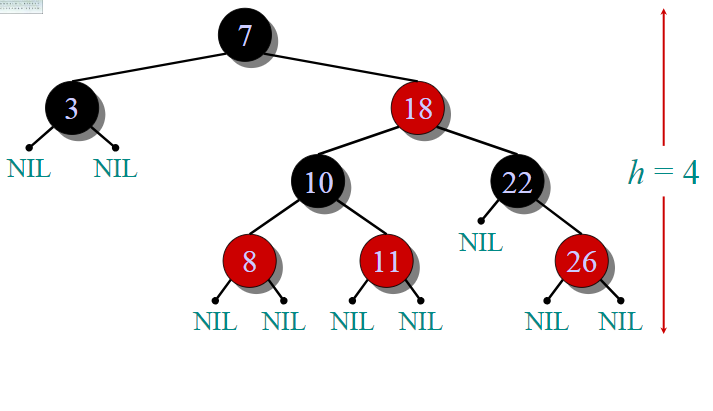
This data structure requires an extra one-bit color field in each node.
Red-black properties:
1. Every node is either red or black.
2. The root and leaves (NIL’s) are black.
3. If a node is red, then its parent is black.
4. All simple paths from any node x to a descendant leaf have the same number of black nodes = black-height(x).
http://pages.cs.wisc.edu/~skrentny/cs367-common/readings/Red-Black-Trees/index.html
Recall that, for binary search trees, although the average-case times for the lookup, insert, and delete methods are all O(log N), where N is the number of nodes in the tree, the worst-case time is O(N). We can guarantee O(log N) time for all three methods by using a balanced tree -- a tree that always has height O(log N)-- instead of a binary search tree.
A number of different balanced trees have been defined, including AVL trees, 2-4 trees, and B trees. You might learn about the first two in an algorithms class and the third in a database class. Here we will look at yet another kind of balanced tree called a red-black tree.
The important idea behind all of these trees is that the insert and delete operations may restructure the tree to keep it balanced. So lookup, insert, and delete will always be logarithmic in the number of nodes but insert and delete may be more complicated than for binary search trees.
A red-black tree is a binary search tree in which
- each node has a color (red or black) associated with it (in addition to its key and left and right children)
- the following 3 properties hold:
- (root property) The root of the red-black tree is black
- (red property) The children of a red node are black.
- (black property) For each node with at least one null child, the number of black nodes on the path from the root to the null child is the same.
An example of a red-black tree is shown below:

https://baike.baidu.com/item/红黑树
- 中文名
- 红黑树
- 外文名
- RED-BLACK-TREE
- 性 质
- 自平衡二叉查找树
- 用 途
- 实现关联数组
- 发明人
- 鲁道夫·贝尔
- 发明时间
- 1972年
- 别 名
- 对称二叉B树
数据结构
质。
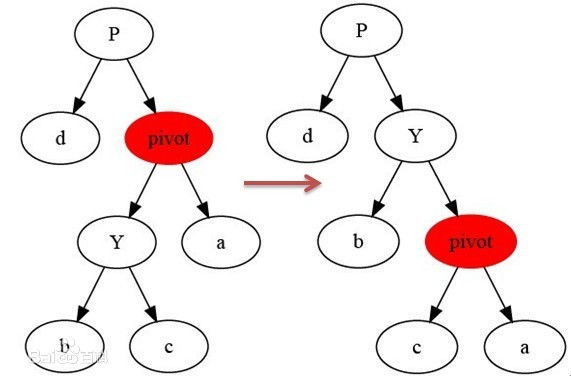
树的左旋

树的右旋
性质
术语
用途
操作
https://zh.wikipedia.org/wiki/平衡树
平衡树是计算机科学中的一类数据结构,为改进的二叉查找树。一般的二叉查找树的查询复杂度取决于目标结点到树根的距离(即深度),因此当结点的深度普遍较大时,查询的均摊复杂度会上升。为了实现更高效的查询,产生了平衡树。
在这里,平衡指所有叶子的深度趋于平衡,更广义的是指在树上所有可能查找的均摊复杂度偏低。
不平衡的树结构
平衡的树结构

基本操作
旋转(rotate):几乎所有平衡树的操作都基于树旋转操作(也有部分基于重构,如替罪羊树),通过旋转操作可以使得树趋于平衡。对一棵查找树(search tree)进行查询、新增、删除等动作,所花的时间与树的高度h成比例,并不与树的容量n成比例。如果可以让树维持平衡,也就是让h维持在O(logN)的左右,就可以在O(logN)的复杂度内完成各种基本操作[1]。
插入(insert):在树中插入一个新值。
删除(delete):在树中删除一个值。
查询前驱(predecessor):前驱定义为小于x,且最大的数。
查询后继(successor):后继定义为大于x,且最小的数。
在维护节点大小(size)后,可以支持以下操作:
查询排名(rank):排名定义为比x小的数的个数加一。
查询第k大:即排名为k的数。
各种平衡树
- AVL树:是最早被发明的自平衡二叉查找树。在AVL树中,任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是O(logN)。增加和删除元素的操作则可能需要借由一次或多次树旋转,以实现树的重新平衡。AVL树得名于它的发明者G. M. Adelson-Velsky和Evgenii Landis,他们在1962年的论文An algorithm for the organization of information 中公开了这一数据结构。 节点的平衡因子是它的左子树的高度减去它的右子树的高度(有时相反)。带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子 -2或2的节点被认为是不平衡的,并需要重新平衡这个树。平衡因子可以直接存储在每个节点中,或从可能存储在节点中的子树高度计算出来。
- 树堆(Treap):是有一个随机附加域满足堆的性质的二叉搜索树,其结构相当于以随机数据插入的二叉搜索树。其基本操作的期望时间复杂度为O(logN)。相对于其他的平衡二叉搜索树,Treap的特点是实现简单,且能基本实现随机平衡的结构。
- 伸展树(Splay tree):能在均摊O(logN)的时间内完成基于伸展(Splay)操作的插入、查找、修改和删除操作。它是由丹尼尔·斯立特(Daniel Sleator)和罗伯特·塔扬在1985年发明的。在伸展树上的一般操作都基于伸展操作:假设想要对一个二叉查找树执行一系列的查找操作,为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法,在每次查找之后对树进行调整,把被查找的条目搬移到离树根近一些的地方。伸展树应运而生。伸展树是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去。 它的优势在于不需要记录用于平衡树的冗余信息。
- 红黑树 (Red–black tree):在1972年由鲁道夫·贝尔发明,被称为"对称二叉B树",它现代的名字源于Leo J. Guibas和Robert Sedgewick于1978年写的一篇论文。红黑树的结构复杂,但它的操作有着良好的最坏情况运行时间,并且在实践中高效:它可以在O(logN)时间内完成查找,插入和删除,这里的n是树中元素的数目。
- 加权平衡树(Weight balanced tree):加权平衡树的每个结点储存这个结点下子树的大小,可以用来实现顺序统计树操作。优势在于占用空间相对较小。
- 2-3树:其内部节点(存在子节点的节点)要么有2个孩子和1个数据元素,要么有3个孩子和2个数据元素,叶子节点没有孩子,并且有1个或2个数据元素。2–3树和AA树是等距同构的,换句话说,对于每个2–3树,都至少有1个AA树和它的元素排列是相同的。
- AA树:AA树是红黑树的一种变种,是Arne Andersson教授在1993年年在他的论文"Balanced search trees made simple"中介绍,设计的目的是减少红黑树考虑的不同情况,区别于红黑树的是,AA树的红节点只能作为右叶子,从而大大简化了维护2-3树的模拟。
- 替罪羊树:其平衡基于部分重建,在非平衡的二叉搜索树中,每次操作以后检查操作路径,找到最高的满足左右子树大小大于平衡因子(alpha)乘以自身大小的结点,重建整个子树。这样就得到了替罪羊树,而被重建的子树的原来的根就被称为替罪羊节点。
其他类型
以下数据结构支持平衡树大多数操作,但实现有根本不同:
应用
用于表示有序的线性数据结构,如优先队列、关联数组、键(key)-值(value)的映射等。自平衡的二叉查找树与哈希表的相比,各有优缺。平衡树在按序遍历所有键值时是量级最优的,哈希表不能。自平衡二叉查找树在查找一个键值时,最坏情况下时间复杂度优于哈希表,O(logN)对比O(logN);但平均时间复杂度逊于hash表,O(logN)对比O(log1)。
平衡树的排序方法,虽然在平均时间复杂度上也是O(nlogN),但由于cache性能、树的调整操作等,性能上不如快速排序、堆排序、归并排序等同为O(nlogN)复杂度的排序。
参考文献
- ^ 跳转至:1.0 1.1 Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Second Edition. Addison-Wesley, 1998. ISBN 0-201-89685-0. Section 6.2.3: Balanced Trees, pp.458–481.



