负数表示法 原码 反码 补码 C语言整数 带符号整数 浮点数 浮点精度 IEEE754


单精度 双精度



小结:
1、为什么有补码:解决 正负相加为0。
3+(-3)=0
x+(-x)=0
对x各位取反,之后和原x且运算
则,各位均为1,此时不为0,
此时再+1,则为0。
补码:无论x正负、0,各位取反,再加1,即得到补码。
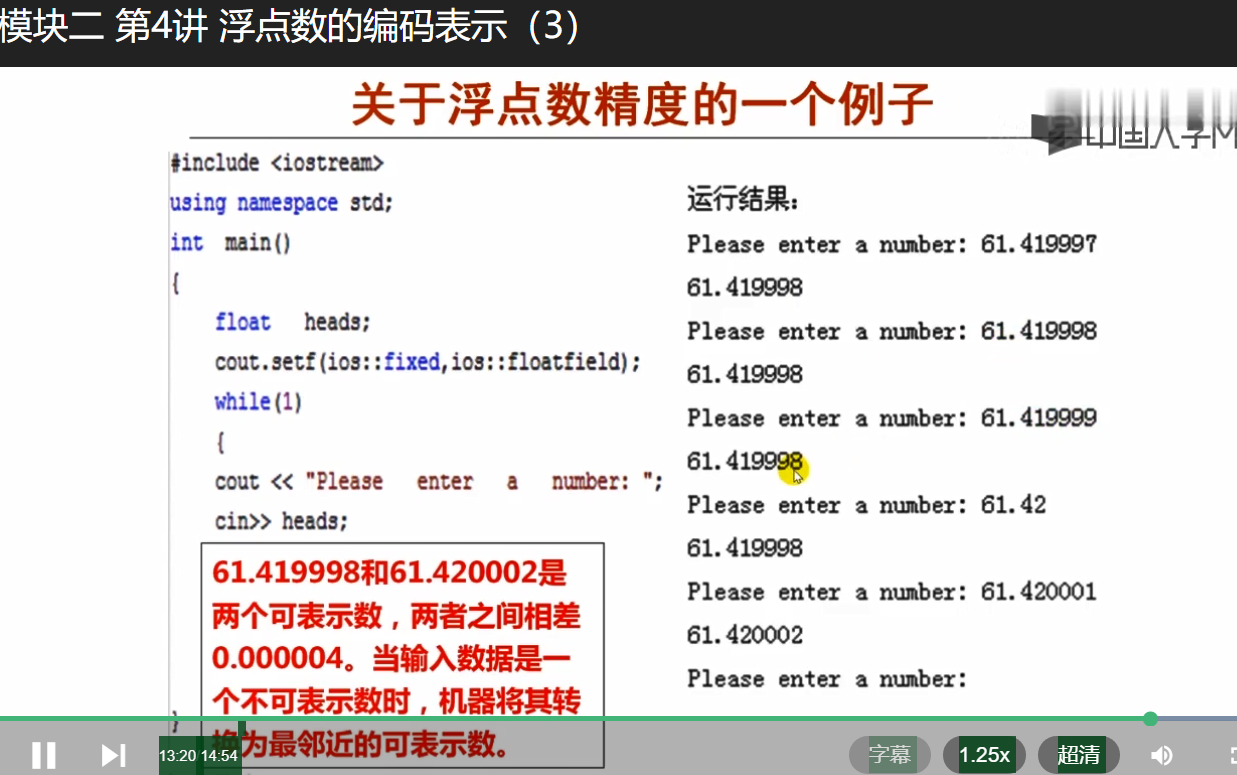


计算机系统基础(一):程序的表示、转换与链接-模块二 第4讲 浮点数的编码表示(2)-网易公开课 https://open.163.com/newview/movie/free?pid=WFVPGEQSL&mid=GFVPGEVLP

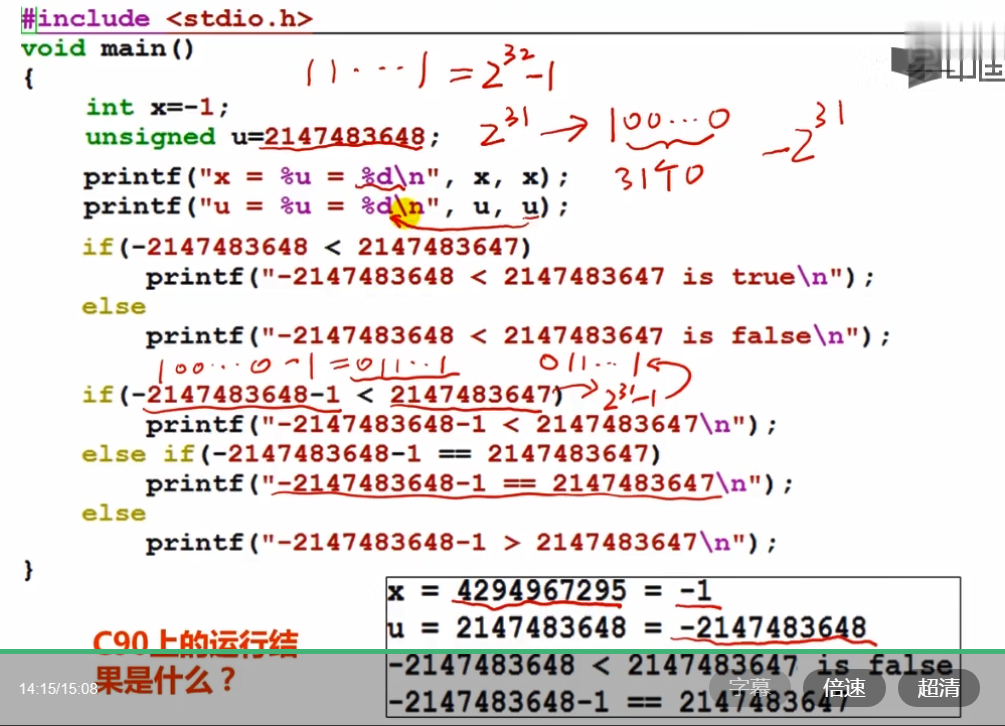

补码运算系统是模运算系统 加减运算统一
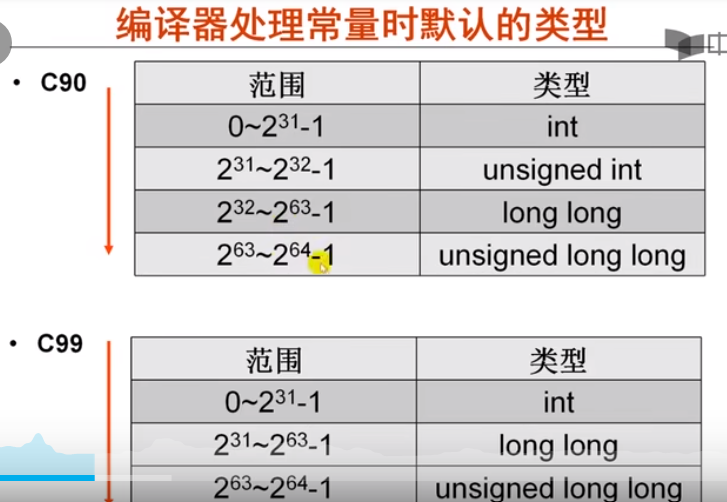


有符号数和无符号数比较,编译器转化为无符号数比较。
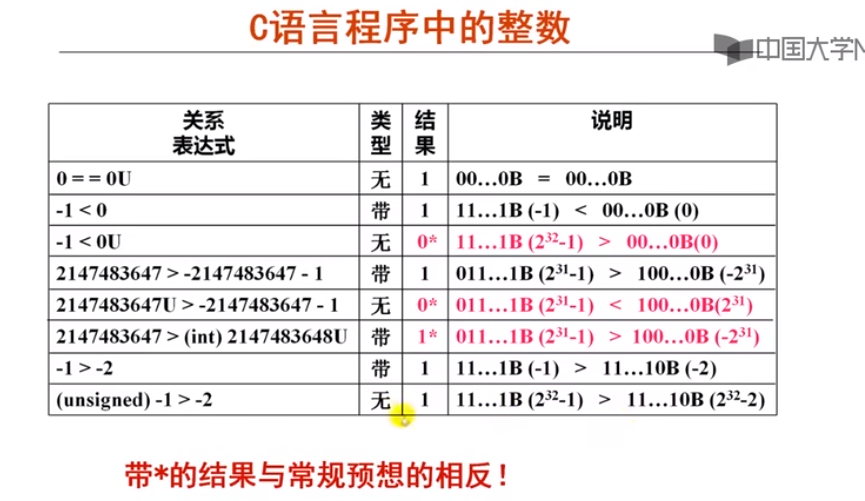
计算机系统基础(一):程序的表示、转换与链接-模块二 第2讲 定点数的编码表示(3)-网易公开课 https://open.163.com/newview/movie/free?pid=WFVPGEQSL&mid=VFVPGEUM3

还搞不懂负数怎么用二进制表示?看完这一篇就懂了 - 知乎 https://zhuanlan.zhihu.com/p/150291780
4
100
-4
32位:
4取反
1111 1111 1111 1111
1111 1111 1111 1111
1111 1111 1111 1111
1111 1111 1111 1011
+1
1111 1111 1111 1111
1111 1111 1111 1111
1111 1111 1111 1111
1111 1111 1111 1100
9
1001
-9
9取反
1111 1111 1111 1111
1111 1111 1111 1111
1111 1111 1111 1111
1111 1111 1111 0110
+1
1111 1111 1111 1111
1111 1111 1111 1111
1111 1111 1111 1111
1111 1111 1111 0111
负数: 绝对值正数的二进制的补码表示
学过计算机组成原理的小伙伴们都知道,在计算机中,负数的二进制是用2的补码表示负数的。
那么,为什么要用这种方式表示负数?有什么好处?
我们一起来看下吧。
为什么用这种方式表示负数
计算机的内存通常都是由8位的字节构成的,所以一个二进制数要存储在很多个的8位的内存中,而通常都是最左边的位为符号位,0表示正,1表示负数。所以不管数字是8位,16位,还是32位,通常都会认为最左边的比特为符号位。
如下图表示:
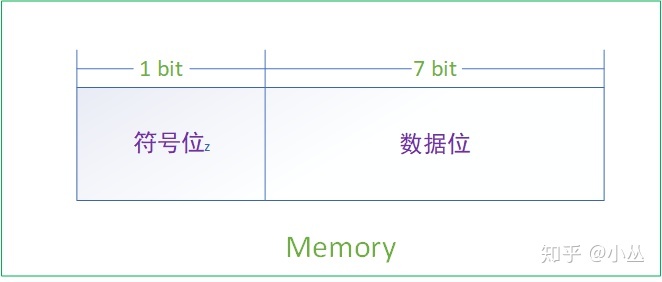
这种方法看起来是解决了问题,在某些计算机上也确实解决了问题。每个数字由符号位的数据位组成,符号位为0表示正数,而1表示负数。数据位只是表示该数据的绝对值。
其实,这种方法只能用于无符号数值的加法运算,即正数加正数,能正确表示出来,要是要执行减法运算,就会出现问题。不信的话,看下面的例子吧。
现在假设用-8去加12,在计算机中,我们用理项状态下的简单的加法电路的方法去加,会发生什么?
以二进制表示+12为00001100;
以二进制表示 -8(假设情况下) 为10001000;
相加结果如下:

所以结果是-20,是不是很出乎意料?
或许有小伙伴看出问题了,上述中把符号位一起进行相加处理了。那么我们反过来想一下。或许就有答案了。
我们用+4去减掉+12,看一下-8在计算机中是怎么表示的。
以二进制表示+4是00000100;
以二进制表示+12是00001100;
那么,相减的结果是什么呢?

`看起来好像不像对不对,但是它就是-8.
`这里的-8的二进制序列,就是2的补码形式。它表示二进制负数。
那么,补码表示法是怎么计算出来的?
从+9的二进制入手:
00001001
现在对每个二进制取反,将变成,变成0:
11110110
这就叫做1的二进制的补码形式,给这个数加上1,就能得到2的二进制补码形式
11110111
那么,回到原题,我们用-8加到+12上的普通运算:
以二进制表示+12是00001100;
以二进制表示-8是11111000;
加到一起,就是

化为10进制,就是+4.
所以,这种方法是有效的。进位会传递到最左边的所有1上,把他们同时设置为0,所以正确的表示了这种计算方式。
这种方式有什么好处
对于计算机来说,最简便的方法就是最好的办法。使用2进制补码是最高效的办法,使用它的原因是,所有的加法计算都可以用同一种电路完成。上面的例子中,用理想状态下的方法去计算,会得到-20,这并不是正确的结果。所以,这说明了正常的加法运算并不适合正数与负数的加法运算,所以,就需要确定两套规则了,正数加正数,正数加负数,那么,就有两种电路了。
而使用2进制的补码形式,可以用正常的方法去运算,只需要将式子改写成12+(-8)= ? ,这样一来,一套电路就可以实现全部整数的加法了。只需要再开发个补码电路,就可以用一套加法电路实现所有加法运算。
https://baike.baidu.com/item/负数表示法/20855568
- 中文名
- 负数表示法
- 外文名
- negative number representation
- 符号位
- 用1表示
- 表示方法
- 原码、反码、补码
- 类 型
- 十进制数
- 应用学科
- 计算机原理
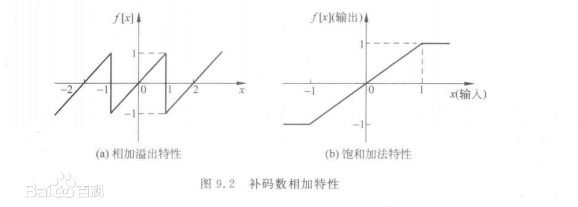
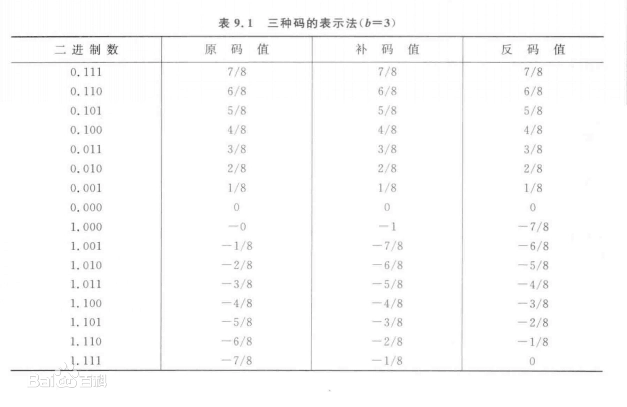
原码
补码




反码








 浙公网安备 33010602011771号
浙公网安备 33010602011771号