调度器 堆 优先级队列 数据结构的堆和栈 非完全二叉树 优先队列 堆队列优先队列

 

GO语言heap剖析及利用heap实现优先级队列 - 随风飘雪012 - 博客园 https://www.cnblogs.com/huxianglin/p/6925119.html

数据结构STL——golang实现优先队列priority_queue - 知乎 https://zhuanlan.zhihu.com/p/425095786

GO语言heap剖析及利用heap实现优先级队列

 

GO语言heap剖析

本节内容

1. heap使用
2. heap提供的方法
3. heap源码剖析
4. 利用heap实现优先级队列

1. heap使用

在go语言的标准库container中，实现了三中数据类型：heap,list,ring，list在前面一篇文章中已经写了，现在要写的是heap（堆）的源码剖析。

首先，学会怎么使用heap，第一步当然是导入包了，代码如下：

package main

import (
	"container/heap"
	"fmt"
)

这个堆使用的数据结构是最小二叉树，即根节点比左边子树和右边子树的所有值都小。源码里面只是实现了一个接口，它的定义如下：

type Interface interface {
	sort.Interface
	Push(x interface{}) // add x as element Len()
	Pop() interface{}   // remove and return element Len() - 1.
}

从这个接口可以看出，其继承了sort.Interface接口，那么sort.Interface的定义是什么呢？源码如下：

type Interface interface {
	// Len is the number of elements in the collection.
	Len() int
	// Less reports whether the element with
	// index i should sort before the element with index j.
	Less(i, j int) bool
	// Swap swaps the elements with indexes i and j.
	Swap(i, j int)
}

也就是说，我们要使用go标准库给我们提供的heap，那么必须自己实现这些接口定义的方法，需要实现的方法如下：

• Len() int
• Less(i, j int) bool
• Swap(i, j int)
• Push(x interface{})
• Pop() interface{}

实现了这五个方法的数据类型才能使用go标准库给我们提供的heap，下面简单示例为定义一个IntHeap类型，并实现上面五个方法。

type IntHeap []int  // 定义一个类型

func (h IntHeap) Len() int { return len(h) }  // 绑定len方法,返回长度
func (h IntHeap) Less(i, j int) bool {  // 绑定less方法
	return h[i] < h[j]  // 如果h[i]<h[j]生成的就是小根堆，如果h[i]>h[j]生成的就是大根堆
}
func (h IntHeap) Swap(i, j int) {  // 绑定swap方法，交换两个元素位置
	h[i], h[j] = h[j], h[i]
}

func (h *IntHeap) Pop() interface{} {  // 绑定pop方法，从最后拿出一个元素并返回
	old := *h
	n := len(old)
	x := old[n-1]
	*h = old[0 : n-1]
	return x
}

func (h *IntHeap) Push(x interface{}) {  // 绑定push方法，插入新元素
	*h = append(*h, x.(int))
}

针对IntHeap实现了这五个方法之后，我们就可以使用heap了，下面是具体使用方法：

func main() {
	h := &IntHeap{2, 1, 5, 6, 4, 3, 7, 9, 8, 0}  // 创建slice
	heap.Init(h)  // 初始化heap
	fmt.Println(*h)
	fmt.Println(heap.Pop(h))  // 调用pop
	heap.Push(h, 6)  // 调用push
	fmt.Println(*h)
	for len(*h) > 0 {
		fmt.Printf("%d ", heap.Pop(h))
	}

}
输出结果：
[0 1 3 6 2 5 7 9 8 4]
0
[1 2 3 6 4 5 7 9 8 6]
1 2 3 4 5 6 6 7 8 9 

上面就是heap的使用了。

2. heap提供的方法

heap提供的方法不多，具体如下：

h := &IntHeap{3, 8, 6}  // 创建IntHeap类型的原始数据
func Init(h Interface)  // 对heap进行初始化，生成小根堆（或大根堆）
func Push(h Interface, x interface{})  // 往堆里面插入内容
func Pop(h Interface) interface{}  // 从堆顶pop出内容
func Remove(h Interface, i int) interface{}  // 从指定位置删除数据，并返回删除的数据
func Fix(h Interface, i int)  // 从i位置数据发生改变后，对堆再平衡，优先级队列使用到了该方法

3. heap源码剖析

heap的内部实现，是使用最小(最大)堆，索引排序从根节点开始，然后左子树，右子树的顺序方式。 内部实现的down和up分别表示对堆中的某个元素向下保证最小(最大)堆和向上保证最小(最大)堆。

当往堆中插入一个元素的时候，这个元素插入到最右子树的最后一个节点中，然后调用up向上保证最小(最大)堆。

当要从堆中推出一个元素的时候，先吧这个元素和右子树最后一个节点交换，然后弹出最后一个节点，然后对root调用down，向下保证最小(最大)堆。

好了，开始分析源码：

首先，在使用堆之前，必须调用它的Init方法，初始化堆，生成小根(大根)堆。Init方法源码如下:

// A heap must be initialized before any of the heap operations
// can be used. Init is idempotent with respect to the heap invariants
// and may be called whenever the heap invariants may have been invalidated.
// Its complexity is O(n) where n = h.Len().
//
func Init(h Interface) {
	// heapify
	n := h.Len()  // 获取数据的长度
	for i := n/2 - 1; i >= 0; i-- {  // 从长度的一半开始，一直到第0个数据，每个位置都调用down方法，down方法实现的功能是保证从该位置往下保证形成堆
		down(h, i, n)
	}
}

接下来看down的源码：

func down(h Interface, i0, n int) bool {
	i := i0  // 中间变量，第一次存储的是需要保证往下需要形成堆的节点位置
	for {  // 死循环
		j1 := 2*i + 1  // i节点的左子孩子
		if j1 >= n || j1 < 0 { // j1 < 0 after int overflow  // 保证其左子孩子没有越界
			break
		}
		j := j1 // left child  // 中间变量j先赋值为左子孩子，之后j将被赋值为左右子孩子中最小（大）的一个孩子的位置
		if j2 := j1 + 1; j2 < n && !h.Less(j1, j2) {
			j = j2 // = 2*i + 2  // right child
		}  // 这之后，j被赋值为两个孩子中的最小（大）孩子的位置（最小或最大由Less中定义的决定）
		if !h.Less(j, i) {
			break
		}  // 若j大于（小于）i，则终止循环
		h.Swap(i, j)  // 否则交换i和j位置的值
		i = j  // 令i=j，继续循环，保证j位置的子数是堆结构
	}
	return i > i0
}

这是建立堆的核心代码，其实，down并不能完全保证从某个节点往下每个节点都能保持堆的特性，只能保证某个节点的值如果不满足堆的性质，则将该值与其孩子交换，直到该值放到适合的位置，保证该值及其两个子孩子满足堆的性质。

但是，如果是通过Init循环调用down将能保证初始化后所有的节点都保持堆的特性，这是因为循环开始的i := n/2 - 1的取值位置，将会取到最大的一个拥有孩子节点的节点，并且该节点最多只有两个孩子，并且其孩子节点是叶子节点，从该节点往前每个节点如果都能保证down的特性，则整个列表也就符合了堆的性质了。

同样，有down就有up，up保证的是某个节点如果向上没有保证堆的性质，则将其与父节点进行交换，直到该节点放到某个特定位置保证了堆的性质。代码如下：

func up(h Interface, j int) {
	for {  // 死循环
		i := (j - 1) / 2 // parent  // j节点的父节点
		if i == j || !h.Less(j, i) {  // 如果越界，或者满足堆的条件，则结束循环
			break
		}
		h.Swap(i, j)  // 否则将该节点和父节点交换
		j = i  // 对父节点继续进行检查直到根节点
	}
}

以上两个方法就是最核心的方法了，所有暴露出来的方法无非就是对这两个方法进行的封装。我们来看看以下这些方法的源码：

func Push(h Interface, x interface{}) {
	h.Push(x)  // 将新插入进来的节点放到最后
	up(h, h.Len()-1)  // 确保新插进来的节点网上能保证堆结构
}

func Pop(h Interface) interface{} {
	n := h.Len() - 1  // 把最后一个节点和第一个节点进行交换，之后，从根节点开始重新保证堆结构，最后把最后那个节点数据丢出并返回
	h.Swap(0, n)
	down(h, 0, n)
	return h.Pop()
}

func Remove(h Interface, i int) interface{} {
	n := h.Len() - 1  pop只是remove的特殊情况，remove是把i位置的节点和最后一个节点进行交换，之后保证从i节点往下及往上都保证堆结构，最后把最后一个节点的数据丢出并返回
	if n != i {
		h.Swap(i, n)
		down(h, i, n)
		up(h, i)
	}
	return h.Pop()
}

func Fix(h Interface, i int) {
	if !down(h, i, h.Len()) {  // i节点的数值发生改变后，需要保证堆的再平衡，先调用down保证该节点下面的堆结构，如果有位置交换，则需要保证该节点往上的堆结构，否则就不需要往上保证堆结构，一个小小的优化
		up(h, i)
	}
}

以上就是go里面的heap所有的源码了，我也就不贴出完整版源码了，以上理解全部基于个人的理解，如有不当之处，还望批评指正。

4. 利用heap实现优先级队列

既然用到了heap，那就用heap实现一个优先级队列吧，这个功能是很好的一个功能。
源码如下：

package main

import (
	"container/heap"
	"fmt"
)

type Item struct {
	value    string // 优先级队列中的数据，可以是任意类型，这里使用string
	priority int    // 优先级队列中节点的优先级
	index    int    // index是该节点在堆中的位置
}

// 优先级队列需要实现heap的interface
type PriorityQueue []*Item

// 绑定Len方法
func (pq PriorityQueue) Len() int {
	return len(pq)
}

// 绑定Less方法，这里用的是小于号，生成的是小根堆
func (pq PriorityQueue) Less(i, j int) bool {
	return pq[i].priority < pq[j].priority
}

// 绑定swap方法
func (pq PriorityQueue) Swap(i, j int) {
	pq[i], pq[j] = pq[j], pq[i]
	pq[i].index, pq[j].index = i, j
}

// 绑定put方法，将index置为-1是为了标识该数据已经出了优先级队列了
func (pq *PriorityQueue) Pop() interface{} {
	old := *pq
	n := len(old)
	item := old[n-1]
	*pq = old[0 : n-1]
	item.index = -1
	return item
}

// 绑定push方法
func (pq *PriorityQueue) Push(x interface{}) {
	n := len(*pq)
	item := x.(*Item)
	item.index = n
	*pq = append(*pq, item)
}

// 更新修改了优先级和值的item在优先级队列中的位置
func (pq *PriorityQueue) update(item *Item, value string, priority int) {
	item.value = value
	item.priority = priority
	heap.Fix(pq, item.index)
}

func main() {
	// 创建节点并设计他们的优先级
	items := map[string]int{"二毛": 5, "张三": 3, "狗蛋": 9}
	i := 0
	pq := make(PriorityQueue, len(items)) // 创建优先级队列，并初始化
	for k, v := range items {             // 将节点放到优先级队列中
		pq[i] = &Item{
			value:    k,
			priority: v,
			index:    i}
		i++
	}
	heap.Init(&pq) // 初始化堆
	item := &Item{ // 创建一个item
		value:    "李四",
		priority: 1,
	}
	heap.Push(&pq, item)           // 入优先级队列
	pq.update(item, item.value, 6) // 更新item的优先级
	for len(pq) > 0 {
		item := heap.Pop(&pq).(*Item)
		fmt.Printf("%.2d:%s index:%.2d\n", item.priority, item.value, item.index)
	}
}

输出结果：
03:张三 index:-01
05:二毛 index:-01
06:李四 index:-01
09:狗蛋 index:-01

 

分类: golang

 

 

 

 

 

小结：

1、

在优先队列中，元素被赋予优先级。

优先队列具有最高级先出 （first in, largest out）的行为特征。

 

Heaps are arrays for which a[k] <= a[2*k+1] and a[k] <= a[2*k+2] for

all k, counting elements from 0.

 

 

 

 https://en.wikipedia.org/wiki/Binary_heap

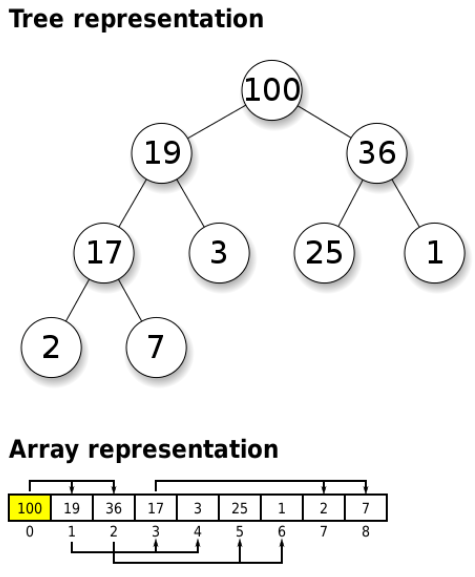
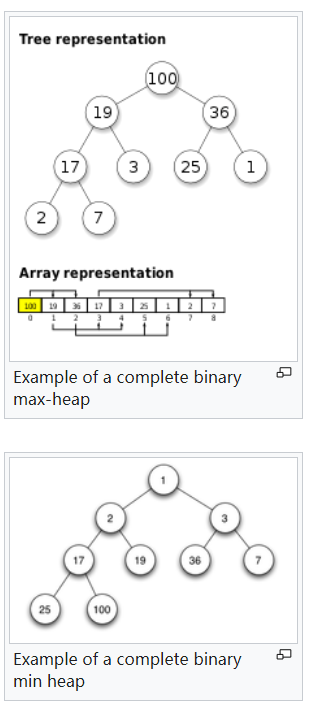
 Example of a complete binary max-heap

 

Example of a complete binary min heap

Binary (min) heap

Type

binary tree/heap

Invented

1964

Invented by

J. W. J. Williams

Time complexity in big O notation

Algorithm		Average	Worst case
Space		O(n)	O(n)
Search		O(n)	O(n)
Insert		O(1)	O(log n)
Find-min		O(1)	O(1)
Delete-min		O(log n)	O(log n)

 

 

 

 heapq — Heap queue algorithm — Python 3.10.4 documentation https://docs.python.org/3/library/heapq.html

 应用：

任务调度

A heapsort can be implemented by pushing all values onto a heap and then popping off the smallest values one at a time:

>>>

>>> def heapsort(iterable):
...     h = []
...     for value in iterable:
...         heappush(h, value)
...     return [heappop(h) for i in range(len(h))]
...
>>> heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0])
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

This is similar to sorted(iterable), but unlike sorted(), this implementation is not stable.

Heap elements can be tuples. This is useful for assigning comparison values (such as task priorities) alongside the main record being tracked:

>>>

>>> h = []
>>> heappush(h, (5, 'write code'))
>>> heappush(h, (7, 'release product'))
>>> heappush(h, (1, 'write spec'))
>>> heappush(h, (3, 'create tests'))
>>> heappop(h)
(1, 'write spec')

 

 优先队列是堆的常见应用

Priority Queue Implementation Notes

A priority queue is common use for a heap, and it presents several implementation challenges:

• Sort stability: how do you get two tasks with equal priorities to be returned in the order they were originally added?

• Tuple comparison breaks for (priority, task) pairs if the priorities are equal and the tasks do not have a default comparison order.

• If the priority of a task changes, how do you move it to a new position in the heap?

• Or if a pending task needs to be deleted, how do you find it and remove it from the queue?

 

 

 

 

调度器 堆 优先级队列

 

堆和栈的理解和区别，C语言堆和栈完全攻略 http://c.biancheng.net/c/stack/ 

数据结构的堆和栈

在数据结构中，栈是一种可以实现“先进后出”（或者称为“后进先出”）的存储结构。假设给定栈 S=（a₀，a₁，…，a_n-1），则称 a₀ 为栈底，a_n-1 为栈顶。进栈则按照 a₀，a₁，…，a_n-1 的顺序进行进栈；而出栈的顺序则需要反过来，按照“后存放的先取，先存放的后取”的原则进行，则 a_n-1 先退出栈，然后 a_n-2 才能够退出，最后再退出 a₀。

在实际编程中，可以通过两种方式来实现：使用数组的形式来实现栈，这种栈也称为静态栈；使用链表的形式来实现栈，这种栈也称为动态栈。

相对于栈的“先进后出”特性，堆则是一种经过排序的树形数据结构，常用来实现优先队列等。假设有一个集合 K={k₀，k₁，…，k_n-1}，把它的所有元素按完全二叉树的顺序存放在一个数组中，并且满足：

 

Python - DS Introduction - Tutorialspoint https://www.tutorialspoint.com/python_data_structure/python_data_structure_introduction.htm

 

Liner Data Structures

These are the data structures which store the data elements in a sequential manner.

• Array: It is a sequential arrangement of data elements paired with the index of the data element.
• Linked List: Each data element contains a link to another element along with the data present in it.
• Stack: It is a data structure which follows only to specific order of operation. LIFO(last in First Out) or FILO(First in Last Out).
• Queue: It is similar to Stack but the order of operation is only FIFO(First In First Out).
• Matrix: It is two dimensional data structure in which the data element is referred by a pair of indices.

Non-Liner Data Structures

These are the data structures in which there is no sequential linking of data elements. Any pair or group of data elements can be linked to each other and can be accessed without a strict sequence.

• Binary Tree: It is a data structure where each data element can be connected to maximum two other data elements and it starts with a root node.
• Heap: It is a special case of Tree data structure where the data in the parent node is either strictly greater than/ equal to the child nodes or strictly less than it’s child nodes.
• Hash Table: It is a data structure which is made of arrays associated with each other using a hash function. It retrieves values using keys rather than index from a data element.
• Graph: .It is an arrangement of vertices and nodes where some of the nodes are connected to each other through links.

 

栈 stack是线性的数据结构

堆 heap是非线性的数据结构

 

 

完全二叉树

 

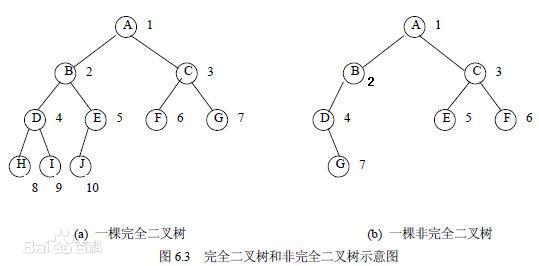
https://baike.baidu.com/item/完全二叉树/7773232

完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

 

 

中文名

完全二叉树

外文名

Complete Binary Tree

实    质

效率很高的数据结构

特    点

叶子结点只可能在最大的两层出现

性    质

度为1的点只有1个或0个

应用学科

计算机科学

 

算法思路

判断一棵树是否是完全二叉树的思路

1>如果树为空，则直接返回错
　　2>如果树不为空：层序遍历二叉树
　　2.1>如果一个结点左右孩子都不为空，则pop该节点，将其左右孩子入队列；
　　2.1>如果遇到一个结点，左孩子为空，右孩子不为空，则该树一定不是完全二叉树；
　　2.2>如果遇到一个结点，左孩子不为空，右孩子为空；或者左右孩子都为空；则该节点之后的队列中的结点都为叶子节点；该树才是完全二叉树，否则就不是完全二叉树；

 

 

class Stack:
    def __init__(self):
        self.stack = []

    def add(self, dataval):
        if dataval not in self.stack:
            self.stack.append(dataval)
            return True
        else:
            return False

    def peek(self):
        return self.stack[-1]

    def remove(self):
        if len(self.stack) <= 0:
            return 'No element in the Stack'
        else:
            return self.stack.pop()


AStack = Stack()
AStack.add('Mon')
AStack.peek()
print(AStack.peek())
AStack.add('Wed')
AStack.add('Thu')
print(AStack.peek())
AStack.remove()



Python - Stack - Tutorialspoint https://www.tutorialspoint.com/python_data_structure/python_stack.htm

 

 

 

py381\Lib\heapq.py

 Python - Heaps - Tutorialspoint https://www.tutorialspoint.com/python_data_structure/python_heaps.htm

 大顶堆 小顶堆

 二元竞标赛（binary tournament）

"""Heap queue algorithm (a.k.a. priority queue).

Heaps are arrays for which a[k] <= a[2*k+1] and a[k] <= a[2*k+2] for
all k, counting elements from 0.  For the sake of comparison,
non-existing elements are considered to be infinite.  The interesting
property of a heap is that a[0] is always its smallest element.

Usage:

heap = []            # creates an empty heap
heappush(heap, item) # pushes a new item on the heap
item = heappop(heap) # pops the smallest item from the heap
item = heap[0]       # smallest item on the heap without popping it
heapify(x)           # transforms list into a heap, in-place, in linear time
item = heapreplace(heap, item) # pops and returns smallest item, and adds
                               # new item; the heap size is unchanged

Our API differs from textbook heap algorithms as follows:

- We use 0-based indexing.  This makes the relationship between the
  index for a node and the indexes for its children slightly less
  obvious, but is more suitable since Python uses 0-based indexing.

- Our heappop() method returns the smallest item, not the largest.

These two make it possible to view the heap as a regular Python list
without surprises: heap[0] is the smallest item, and heap.sort()
maintains the heap invariant!
"""

# Original code by Kevin O'Connor, augmented by Tim Peters and Raymond Hettinger

__about__ = """Heap queues

[explanation by François Pinard]

Heaps are arrays for which a[k] <= a[2*k+1] and a[k] <= a[2*k+2] for
all k, counting elements from 0.  For the sake of comparison,
non-existing elements are considered to be infinite.  The interesting
property of a heap is that a[0] is always its smallest element.

The strange invariant above is meant to be an efficient memory
representation for a tournament.  The numbers below are `k', not a[k]:

                                   0

                  1                                 2

          3               4                5               6

      7       8       9       10      11      12      13      14

    15 16   17 18   19 20   21 22   23 24   25 26   27 28   29 30


In the tree above, each cell `k' is topping `2*k+1' and `2*k+2'.  In
a usual binary tournament we see in sports, each cell is the winner
over the two cells it tops, and we can trace the winner down the tree
to see all opponents s/he had.  However, in many computer applications
of such tournaments, we do not need to trace the history of a winner.
To be more memory efficient, when a winner is promoted, we try to
replace it by something else at a lower level, and the rule becomes
that a cell and the two cells it tops contain three different items,
but the top cell "wins" over the two topped cells.

If this heap invariant is protected at all time, index 0 is clearly
the overall winner.  The simplest algorithmic way to remove it and
find the "next" winner is to move some loser (let's say cell 30 in the
diagram above) into the 0 position, and then percolate this new 0 down
the tree, exchanging values, until the invariant is re-established.
This is clearly logarithmic on the total number of items in the tree.
By iterating over all items, you get an O(n ln n) sort.

A nice feature of this sort is that you can efficiently insert new
items while the sort is going on, provided that the inserted items are
not "better" than the last 0'th element you extracted.  This is
especially useful in simulation contexts, where the tree holds all
incoming events, and the "win" condition means the smallest scheduled
time.  When an event schedule other events for execution, they are
scheduled into the future, so they can easily go into the heap.  So, a
heap is a good structure for implementing schedulers (this is what I
used for my MIDI sequencer :-).

Various structures for implementing schedulers have been extensively
studied, and heaps are good for this, as they are reasonably speedy,
the speed is almost constant, and the worst case is not much different
than the average case.  However, there are other representations which
are more efficient overall, yet the worst cases might be terrible.

Heaps are also very useful in big disk sorts.  You most probably all
know that a big sort implies producing "runs" (which are pre-sorted
sequences, which size is usually related to the amount of CPU memory),
followed by a merging passes for these runs, which merging is often
very cleverly organised[1].  It is very important that the initial
sort produces the longest runs possible.  Tournaments are a good way
to that.  If, using all the memory available to hold a tournament, you
replace and percolate items that happen to fit the current run, you'll
produce runs which are twice the size of the memory for random input,
and much better for input fuzzily ordered.

Moreover, if you output the 0'th item on disk and get an input which
may not fit in the current tournament (because the value "wins" over
the last output value), it cannot fit in the heap, so the size of the
heap decreases.  The freed memory could be cleverly reused immediately
for progressively building a second heap, which grows at exactly the
same rate the first heap is melting.  When the first heap completely
vanishes, you switch heaps and start a new run.  Clever and quite
effective!

In a word, heaps are useful memory structures to know.  I use them in
a few applications, and I think it is good to keep a `heap' module
around. :-)

--------------------
[1] The disk balancing algorithms which are current, nowadays, are
more annoying than clever, and this is a consequence of the seeking
capabilities of the disks.  On devices which cannot seek, like big
tape drives, the story was quite different, and one had to be very
clever to ensure (far in advance) that each tape movement will be the
most effective possible (that is, will best participate at
"progressing" the merge).  Some tapes were even able to read
backwards, and this was also used to avoid the rewinding time.
Believe me, real good tape sorts were quite spectacular to watch!
From all times, sorting has always been a Great Art! :-)
"""







数据结构与算法(4)——优先队列和堆 - 我没有三颗心脏 - 博客园 https://www.cnblogs.com/wmyskxz/p/9301021.html

 https://baike.baidu.com/item/优先队列/9354754?fr=aladdin

优先队列(priority queue)

普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出 （first in, largest out）的行为特征。通常采用堆数据结构来实现。

 

中文名

优先队列

外文名

priority queue

特    点

元素被赋予优先级

类    型

数据结构

定    义

一种先进先出的数据结构，元素在队列尾追加，而从队列头删除

实现方式

通常采用堆数据结构

 

 

 

 

 

 

 

可以将优先级队列想象为已修改的队列，但是当一个人从队列中获取下一个元素时，将首先检索优先级最高的元素。

堆栈和队列可以被建模为特定类型的优先级队列。提醒一下，堆栈和队列的行为方式如下：

堆栈 - 元素以最后一个顺序被拉入（例如，一叠纸）

队列 - 元素先进先出（例如，自助餐厅中的一条线）

在堆栈中，每个插入元素的优先级是单调递增的;因此，插入的最后一个元素始终是第一个检索的元素。在队列中，每个插入元素的优先级是单调递减的;因此，插入的第一个元素始终是第一个检索到的元素

 

有限的元素集合,每个元素都有一个优先权

操作

Create ( ):创建一个空的优先队列

Size ( ):返回队列中的元素数目

Max ( ):返回具有最大优先权的元素

Insert (x):将x插入队列

DeleteMax (x):从队列中删除具有最大优先权的元素,并将该元素返回至x

}

优先队列插入和删除元素的复杂度都是O(log2n)，所以很快。

另一种描述方法是采用有序线性表,当元素按递增次序排列,使用链表时则按递减次序排列,这两种描述方法的删除时间均为( 1 ),插入操作所需时间为(n).

例：

假设我们对机器服务进行收费.每个用户每次使用机器所付费用都是相同的,但每个

用户所需要服务时间都不同.为获得最大利润,假设只要有用户机器就不会空闲,我们可以把

等待使用该机器的用户组织成一个最小优先队列,优先权即为用户所需服务时间.当一个新的

用户需要使用机器时,将他/她的请求加入优先队列.一旦机器可用,则为需要最少服务时间

(即具有最高优先权)的用户提供服务.

如果每个用户所需时间相同,但用户愿意支付的费用不同,则可以用支付费用作为优先权,

一旦机器可用,所交费用最多的用户可最先得到服务,这时就要选择最大优先队列.

 

 

 

优先队列的应用

• 数据压缩：赫夫曼编码算法；
• 最短路径算法：Dijkstra算法；
• 最小生成树算法：Prim算法；
• 事件驱动仿真：顾客排队算法；
• 选择问题：查找第k个最小元素；
• 等等等等....

 

 

 

 

 

 

 

 

 

搜索

复制