分位数 四分位距 分位数回归 箱形图
分位数 四分位距 分位数回归
分位数（Quantile），亦称分位点，是指将一个随机变量的概率分布范围分为几个等份的数值点，常用的有中位数（即二分位数）、四分位数、百分位数等。
分位数指的就是连续分布函数中的一个点，这个点对应概率p。若概率0<p<1，随机变量X或它的概率分布的分位数Za，是指满足条件p(X≤Za)=α的实数 。、、、
分布函数（英文Cumulative Distribution Function, 简称CDF），是概率统计中重要的函数，正是通过它，可用数学分析的方法来研究随机变量。分布函数是随机变量最重要的概率特征，分布函数可以完整地描述随机变量的统计规律，并且决定随机变量的一切其他概率特征。
对于任意实数
,
https://baike.baidu.com/item/箱形图/0?fromModule=lemma_inlink
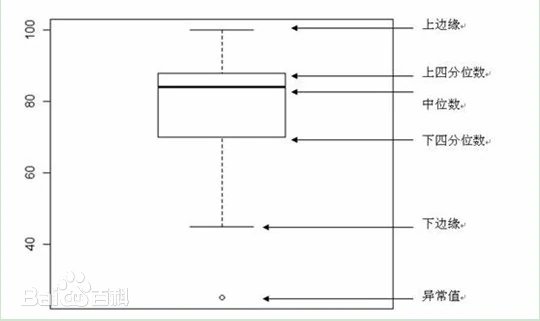
箱形图提供了一种只用5个点对数据集做简单总结的方式。这5个点包括中点、Q1、Q3、分部状态的高位和低位。箱形图很形象的分为中心、延伸以及分布状态的全部范围。
箱形图中最重要的是对相关统计点的计算,相关统计点都可以通过百分位计算方法进行实现。
箱形图的绘制步骤： [2]
3、在Q3+1.5IQR和Q1－1.5IQR处画两条与中位线一样的线段，这两条线段为异常值截断点，称其为内限；在Q3+3IQR和Q1－3IQR处画两条线段，称其为外限。处于内限以外位置的点表示的数据都是异常值，其中在内限与外限之间的异常值为温和的异常值（mild outliers），在外限以外的为极端的异常值(extreme outliers)。四分位距IQR=Q3-Q1。.
4、从矩形盒两端边向外各画一条线段直到不是异常值的最远点，表示该批数据正常值的分布区间。
5、用“〇”标出温和的异常值，用“*”标出极端的异常值。相同值的数据点并列标出在同一数据线位置上，不同值的数据点标在不同数据线位置上。至此一批数据的箱形图便绘出了。统计软件绘制的箱形图一般没有标出内限和外限。
数据异常值
一批数据中的异常值值得关注，忽视异常值的存在是十分危险的，不加剔除地把异常值包括进数据的计算分析过程中，对结果会带来不良影响；重视异常值的出现，分析其产生的原因，常常成为发现问题进而改进决策的契机。箱形图为我们提供了识别异常值的一个标准：异常值被定义为小于Q1－1.5IQR或大于Q3+1.5IQR的值。虽然这种标准有点任意性，但它来源于经验判断，经验表明它在处理需要特别注意的数据方面表现不错。这与识别异常值的经典方法有些不同。众所周知，基于正态分布的3σ法则或z分数方法是以假定数据服从正态分布为前提的，但实际数据往往并不严格服从正态分布。它们判断异常值的标准是以计算数据批的均值和标准差为基础的，而均值和标准差的耐抗性极小，异常值本身会对它们产生较大影响，这样产生的异常值个数不会多于总数0.7%。显然，应用这种方法于非正态分布数据中判断异常值，其有效性是有限的。箱形图的绘制依靠实际数据，不需要事先假定数据服从特定的分布形式，没有对数据作任何限制性要求，它只是真实直观地表现数据形状的本来面貌；另一方面，箱形图判断异常值的标准以四分位数和四分位距为基础，四分位数具有一定的耐抗性，多达25%的数据可以变得任意远而不会很大地扰动四分位数，所以异常值不能对这个标准施加影响，箱形图识别异常值的结果比较客观。由此可见，箱形图在识别异常值方面有一定的优越性。
