仓库选址问题 无约束条件下 最值 Nelder-Mead simplex algorithm
MATLAB实战 | 仓库选址问题(附视频) https://mp.weixin.qq.com/s/uIEmBJGcIm7AK4qsW0n2Aw
https://en.wikipedia.org/wiki/Nelder%E2%80%93Mead_method
fminsearch implements the Nelder-Mead method, see Matlab document: http://www.mathworks.com/help/matlab/ref/fminsearch.html. In the reference section.
To find its equivalent in scipy, you just need to check the doc strings of the methods provided in scipy.optimize. See: http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fmin.html#scipy.optimize.fmin. fmin also implements Nelder-Mead method.
The Nelder–Mead method (also downhill simplex method, amoeba method, or polytope method) is a numerical method used to find the minimum or maximum of an objective function in a multidimensional space. It is a direct search method (based on function comparison) and is often applied to nonlinear optimization problems for which derivatives may not be known. However, the Nelder–Mead technique is a heuristic search method that can converge to non-stationary points[1] on problems that can be solved by alternative methods.[2]
The Nelder–Mead technique was proposed by John Nelder and Roger Mead in 1965,[3] as a development of the method of Spendley et al.[4]
python - numpy/scipy analog of matlab's fminsearch - Stack Overflow https://stackoverflow.com/questions/19070943/numpy-scipy-analog-of-matlabs-fminsearch
Uses a Nelder-Mead simplex algorithm to find the minimum of function of one or more variables.
This algorithm has a long history of successful use in applications. But it will usually be slower than an algorithm that uses first or second derivative information. In practice, it can have poor performance in high-dimensional problems and is not robust to minimizing complicated functions. Additionally, there currently is no complete theory describing when the algorithm will successfully converge to the minimum, or how fast it will if it does. Both the ftol and xtol criteria must be met for convergence.
01
应用实战
【例7-19】仓库选址问题。某公司有A、B、C、D、E共5个工厂,分别位于xy平面上的坐标点(10,10)、(30,50)、(16.667,29)、(0.555,29.888)和(22.2221,49.988)处。设两点之间的距离表示在工厂之间开车的距离,以千米为单位。公司计划在平面上某点处建造一座仓库,预期平均每周到A、B、C、D、E工厂分别有10、18、20、14和25次送货。理想情况下,要使每周送货车的里程最小,仓库应建在xy平面的什么位置?
这是一个无约束最优化问题。总里程既取决于仓库与5个工厂之间的距离,也取决于送货车每周向5个工厂送货的次数,相当于权重。假设仓库所选点的坐标为(x,y),则总里程表达式为:
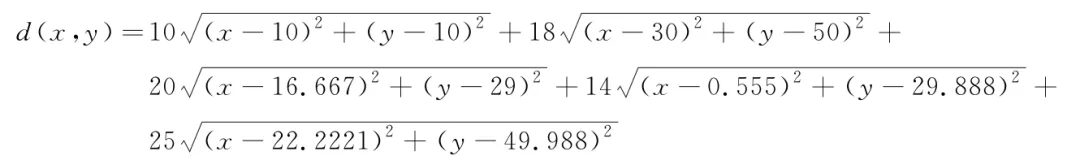
所以原问题即求无约束条件下d(x,y)的最小值。
用向量a表示5个工厂的横坐标,向量b表示5个工厂的纵坐标,向量c表示预期平均每周向5个工厂送货的次数,定义目标函数,调用fminsearch或fmincon函数求解。程序如下:
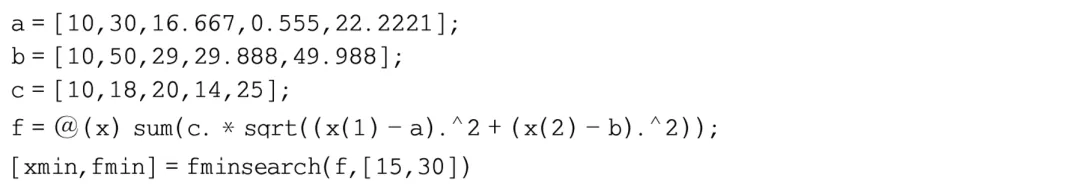
程序运行结果如下:

所以当仓库建在坐标点(19.8143,41.1247)处时,有最小距离为1.3618e+03千米。



