差分数组 前缀和数组
小结：
1、
有数组d=[1,2,3,4,5,6]，对d[2]到d[4]之间的所有数加上3，变为d=[1,2,6,7,8,6]，那么差分数组也就从[1,1,1,1,1,1]变成了[1,1,4,1,1,-2]
Leetcode刷题笔记——差分数组 - 知乎 https://zhuanlan.zhihu.com/p/478120079
差分数组是与前缀和数组所对应的一种逆操作，类似于求导和积分，也就是说，对差分数组求前缀和，可以得到原数组，同样的，对前缀和数组求差分，也可以得到原数组。
差分数组的性质是：
当我们希望对原数组的某一个区间[l,r]施加一个增量inc时，差分数组d对应的变化是：d[l]增加inc，d[r+1]减少inc，并且这种操作是可以叠加的。
例如：有数组d=[1,2,3,4,5,6]，对d[2]到d[4]之间的所有数加上3，变为d=[1,2,6,7,8,6]，那么差分数组也就从[1,1,1,1,1,1]变成了[1,1,4,1,1,-2]。
也就是说，当我们需要对原数组的不同区间施加不同的增量，我们只要按规则修改差分数组即可。
下面是几个典型的差分数组的应用例子：
1109. 航班预订统计
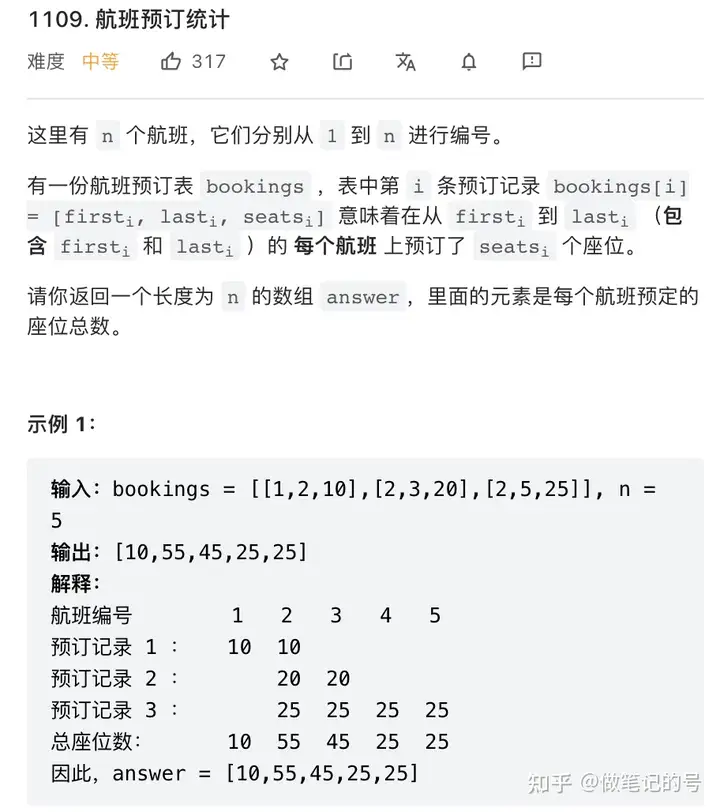
在遍历bookings数组的过程中，我们需要对返回的答案数组不断的做区间增量修改，因此可以使用差分数组来求解。
代码:
class Solution {
public:
vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
//定义差分数组
vector<int> nums(n);
for(auto &booking:bookings){
//在区间的两端对差分数组进行修改，注意bookings的记录从1开始，下标要减去1
nums[booking[0]-1] += booking[2];
if(booking[1]<n){
nums[booking[1]] -= booking[2];
}
}
//计算差分数组的前缀和，得到答案数组
for(int i=1;i<n;i++){
nums[i] += nums[i-1];
}
return nums;
}
};
798. 得分最高的最小轮调
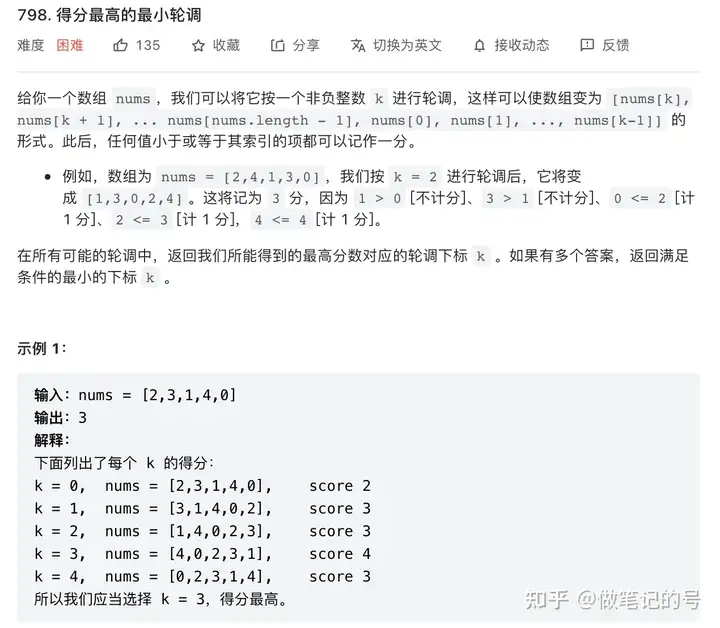
本题首先考虑暴力解法，首先遍历所有可能的k，对下标i，进行轮转之后，新的下标为(i-k+n)%n，计算轮转后的score，选出另score最大的k，复杂度为O(n^2)：
class Solution {
public:
int bestRotation(vector<int>& nums) {
int k=0;
int max_score = INT_MIN;
int n = nums.size();
//枚举k
for(int i=n-1;i>=0;i--){
//算score
int score = 0;
for(int j=0;j<n;j++){
//元素移动后的新下标
int new_idx = (j-i+n)%n;
if(nums[j]<=new_idx){
score++;
}
}
if(score>=max_score){
k=i;
max_score = score;
}
}
return k;
}
};
而这样的方法在数据量比较大的时候会超时。
考虑另一种方法：
对于数组nums 中的每个元素，都可以根据元素值与元素所在下标计算该元素记 1 分的轮调下标范围。遍历所有元素之后，即可得到每个轮调下标对应的计1 分的元素个数，计 1 分的元素个数最多的轮调下标即为得分最高的轮调下标。如果存在多个得分最高的轮调下标，则取其中最小的轮调下标。
所以，可以创建一个长度为n的数组points，points[k]表示轮调为k时的得分，对于数组nums中的每个元素，计算其可以得分的轮调后的下标范围[l,r]，再把points[l]到points[r]范围内的分值加一，这样的区间操作正好可以使用差分数组实现。
由之前的分析可知：下标为i的元素x轮调之后，新的下标为(i-k+n)%n，如果要得分，应该有(i-k+n)%n>=x;
可以得到：k<=(n+i-x)%n，又由(i-k+n)%n<=n-1,得到k>=(i+1)%n，由此，得到：
对于下标为i的元素x，轮训k次可以得分，k的范围为[(i+1)%len,(n+i-x)%n]
class Solution{
public:
int bestRotation(vector<int>& nums){
int len = nums.size();
vector<int> diffs(len);
for (int i = 0; i < len; ++i) {
//计算对于nums[i]进行轮调后，可以加分的k的范围
int low = (i+1)%len;
int high = (i-nums[i]+len+1)%len;
//从low到high区间内所有元素加一，相当于在差分数组上区间两端进行相应操作
diffs[low]++;
diffs[high]--;
if (low >= high){
diffs[0]++;
}
}
int bestIndex = 0;
int maxScore = 0;
int score = 0;
//
for (int i = 0; i < len; ++i) {
score += diffs[i];
if (score > maxScore){
bestIndex = i;
maxScore = score;
}
}
return bestIndex;
}
};
