单调栈 monotonic stack monostack 严格单调 有特殊到一般 归纳推理 特殊化 极端化 左右边界 Both nextSmaller and prevSmaller
小结
1、
Both nextSmaller and prevSmaller
之前、之后的第一个大、小的
func largestRectangleArea(heights []int) int {
/*
1、严格单调栈
2、每个元素都要入栈
序号不连续的原因:缺失的元素比栈顶元素大;尤其当栈底元素不为第一个元素时,说明从第一个元素到。
在元素出栈时求面积
*/
ans := 0
heights = append(heights, 0)
mono := []int{}
for i := 0; i < len(heights); i++ {
toPush := heights[i]
for {
if len(mono) == 0 {
break
}
// 计算待弹出元素为高的区域的左右边界
top := mono[len(mono)-1]
height := heights[top]
if toPush > height {
break
}
var left int
// 左边界
if len(mono) == 1 {
// 左边界为第一个元素
left = 0
} else {
// 左边界为次栈顶元素值+1
left = mono[len(mono)-1-1] + 1
}
// 右边界
right := i - 1
size := height * (right - left + 1)
if size > ans {
ans = size
}
mono = mono[:len(mono)-1]
}
mono = append(mono, i)
}
return ans
}
左边界找对了,但是右边界不对,反例、不通过的用例:1,2,3
func largestRectangleArea(heights []int) int {
/*
1、严格单调栈
2、每个元素都要入栈
序号不连续的原因:缺失的元素比栈顶元素大;尤其当栈底元素不为第一个元素时,说明从第一个元素到。
在元素出栈时求面积
*/
ans := 0
heights = append(heights, 0)
mono := []int{}
for i := 0; i < len(heights); i++ {
toPush := heights[i]
for {
if len(mono) == 0 {
break
}
right := mono[len(mono)-1]
height := heights[right]
if toPush > height {
break
}
var left int
// 左边界
if len(mono) == 1 {
// 左边界为第一个元素
left = 0
} else {
// 左边界为次栈顶元素值+1
left = mono[len(mono)-1-1] + 1
}
size := height * (right - left + 1)
if size > ans {
ans = size
}
mono = mono[:len(mono)-1]
}
mono = append(mono, i)
}
return ans
}
Monotonic Stack - Algorithm https://liuzhenglaichn.gitbook.io/algorithm/monotonic-stack
-
we need to pop smaller elements before pushing.
-
it keep tightening the result as lexigraphically greater as possible. (Because we keep popping smaller elements out and keep greater elements).
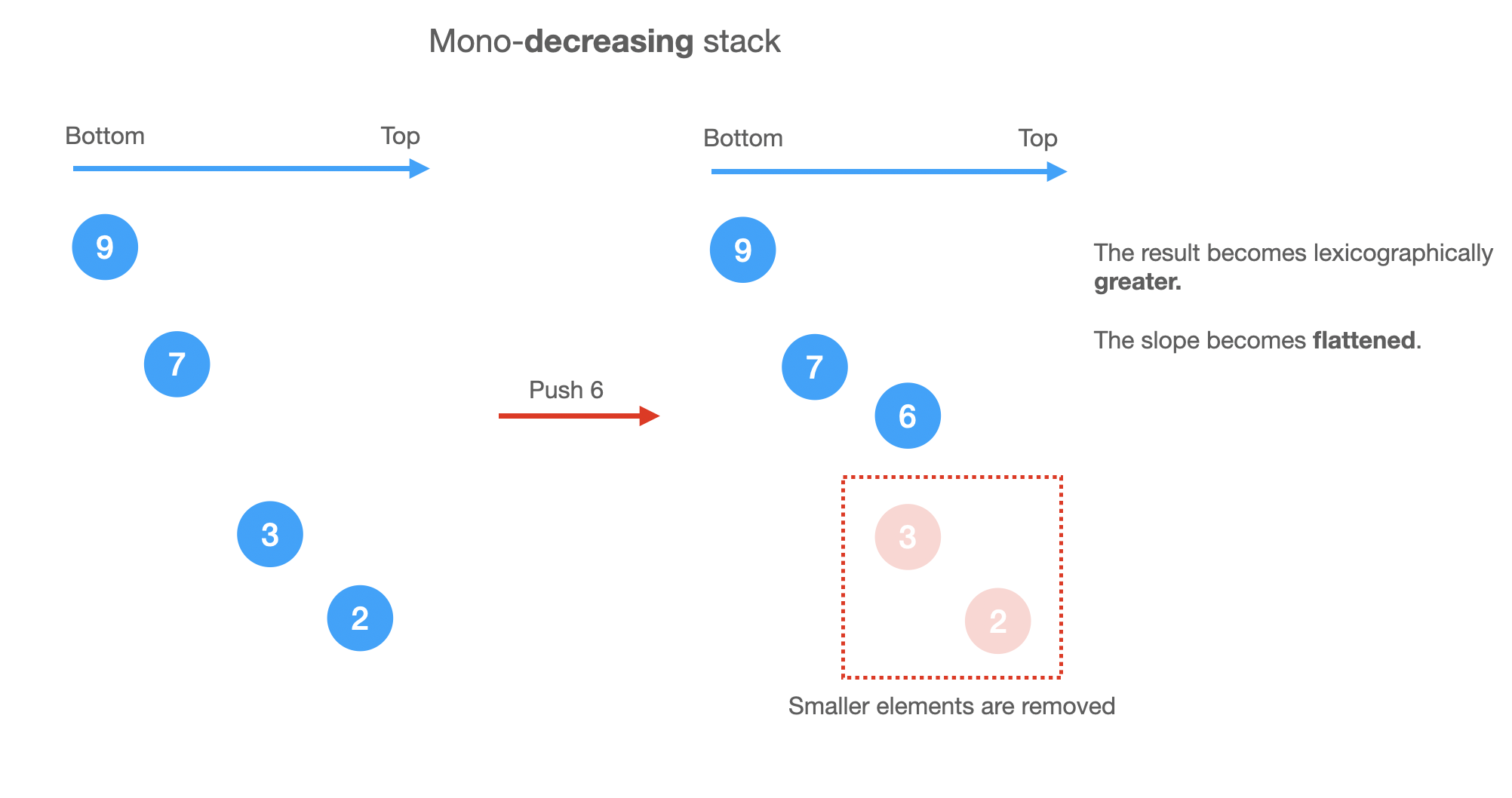
nextSmaller and prevSmaller arrays, we can do it using a mono-stack in one pass.
Largest Rectangular Area in a Histogram | Set 2 - GeeksforGeeks https://www.geeksforgeeks.org/largest-rectangle-under-histogram/
Largest rectangle in histogram - Coding Ninjas CodeStudio https://www.codingninjas.com/codestudio/library/largest-rectangle-in-histogram
Area of largest rectangle in Histogram - Arrays - Tutorial https://takeuforward.org/data-structure/area-of-largest-rectangle-in-histogram/
Largest Rectangle in Histogram - InterviewBit https://www.interviewbit.com/blog/largest-rectangle-in-histogram/
高度呈M形状,两侧足够长
【技巧点拨】经典数据结构:单调栈II https://mp.weixin.qq.com/s/KiPhjpjLjKS_DCnrO09RVg
/*
// OJ: https://leetcode.com/problems/largest-rectangle-in-histogram/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
class Solution {
public:
int largestRectangleArea(vector<int>& A) {
A.push_back(0); // append a zero at the end so that we can pop all elements from the stack and calculate the corresponding areas
int N = A.size(), ans = 0;
stack<int> s; // strictly-increasing mono-stack
for (int i = 0; i < N; ++i) {
while (s.size() && A[i] <= A[s.top()]) { // Take `A[i]` as the right edge
int height = A[s.top()]; // Take the popped element as the height
s.pop();
int left = s.size() ? s.top() : -1; // Take the element left on the stack as the left edge
ans = max(ans, (i - left - 1) * height);
}
s.push(i);
}
return ans;
}
};
*/
func largestRectangleArea(heights []int) int {
var max func(a, b int) int = func(a, b int) int {
if a > b {
return a
}
return b
}
// append a zero at the end so that we can pop all elements from the stack and calculate the corresponding areas
heights = append(heights, 0)
ans := 0
// strictly-increasing mono-stack
mono := []int{}
for i := 0; i < len(heights); i++ {
for {
if !(len(mono) > 0) {
break
}
top := mono[len(mono)-1]
if !(heights[i] <= heights[top]) {
break
}
// Take the popped element as the height
height := heights[top]
mono = mono[:len(mono)-1]
// Take the element left on the stack as the left edge
left := -1
if len(mono) > 0 {
left = mono[len(mono)-1]
}
ans = max(ans, (i-left-1)*height)
}
mono = append(mono, i)
}
return ans
}
{name: "X1", args: args{heights: []int{1, 2, 3}}, want: 4},
{name: "X1-2", args: args{heights: []int{5, 1, 2, 3}}, want: 5},
{name: "X2", args: args{heights: []int{3, 2, 1}}, want: 4},
{name: "X2-2", args: args{heights: []int{3, 2, 1, 1, 1}}, want: 5},
{name: "X2-1", args: args{heights: []int{1, 1, 3, 2, 1}}, want: 5},
{name: "X3", args: args{heights: []int{1, 1, 1}}, want: 3},
{name: "Y1", args: args{heights: []int{1, 0, 2}}, want: 2},
{name: "Y2", args: args{heights: []int{0, 1, 2}}, want: 2},
{name: "M", args: args{heights: []int{1, 1, 1, 8, 4, 1, 4, 8, 1, 1, 1, 1}}, want: 12}, // 高度M形状
小结:
1)
定义
单调栈
对于一列数,所有元素都要入栈,且栈中元素严格单调,即无相等元素。
为了保证栈的严格单调性,就需要考虑已入栈的元素被弹出;
1)新加入元素不大于栈顶元素,则先弹出栈顶元素再入栈;反之,直接入栈。
注意:可能出栈多次,才能入栈。
2)单调性是严格的,栈中无相等的元素。
分析:
遍历每根柱子,
求出高度不低于该高度的柱子(注意不是该根柱子)且包含该高度柱子的柱子连续区间的柱子数(柱子宽均为1),该高度*柱子数=面积。
解:
建立单调递增栈,将柱子高度按顺序入栈。
栈顶元素被弹出前,次栈顶元素的下标+1(如果,栈中只有一个元素,则为第一个元素)即当前连续区间的左边界,将栈顶元素的下标做右边界,求出当前连续区间的面积,和历史最大值比较,即当前此时最大面积;
遍历至最后一根柱子,即的最大面积。
[2,3,1]->(2),(2,3),(1) = (0),(0,1),(2)
[2,5,6,3]->(2),(2,5),(2,5,6),(2,3) = (0),(0,1),(0,1,2),(0,3)
func MonoStackTemperature(l []int) []int {
n := len(l)
ans := make([]int, n, n)
// 建立单调栈
mono := make([]int, 1, 1)
for i := 1; i < n; i++ {
e := l[i]
// 元素入栈
m := len(mono)
for ; m > 0; m-- {
if mono[m-1] > e {
break
} else {
mono = mono[0 : m-1]
}
}
mono = append(mono, e)
// 业务逻辑
for j := 0; j < i; j++ {
if ans[j] == 0 {
if e > l[j] {
ans[j] = i - j
}
}
}
}
return ans
}
func Test_MonoStackTemperature(t *testing.T) {
type args struct {
l []int
}
tests := []struct {
name string
args args
want []int
}{
/*
[2,3,1]->(2),(2,3),(1) = (0),(0,1),(2)-->|1,0,0|
[2,5,6,3]->(2),(2,5),(2,5,6),(2,3) = (0),(0,1),(0,1,2),(0,3)-->|1,1,0,0|
[2,6,5,3]->(2),(2,6),(2,5),(2,3) = (0),(0,1),(0,2),(0,3)-->|1,0,0,0|
[3,2,4]->(3),(2),(2,4) = (0),(1),(1,2)--->|2,1,0|
[8,9,3,2,4]->(8),(8,9),(3),(2),(2,4) = (0),(0,1),(2),(3),(3,4)-->|1,0,2,1,0|
[1,2,3]->(0),(0,1),(0,1,2)-->(1,1,0)
*/
// TODO: Add test cases.
{name: "1", args: args{l: []int{2, 3, 1}}, want: []int{1, 0, 0}},
{name: "2", args: args{l: []int{2, 5, 6, 3}}, want: []int{1, 1, 0, 0}},
{name: "3", args: args{l: []int{2, 6, 5, 3}}, want: []int{1, 0, 0, 0}},
{name: "4", args: args{l: []int{3, 2, 4}}, want: []int{2, 1, 0}},
{name: "5", args: args{l: []int{8, 9, 3, 2, 4}}, want: []int{1, 0, 2, 1, 0}},
{name: "6", args: args{l: []int{1, 2, 3}}, want: []int{1, 1, 0}},
}
for _, tt := range tests {
t.Run(tt.name, func(t *testing.T) {
if got := MonoStackTemperature(tt.args.l); !reflect.DeepEqual(got, tt.want) {
t.Errorf("MonoStackTemperature() = %v, want %v", got, tt.want)
}
})
}
}
注意:上述单调栈没有发挥作用。
选单增、减?
是否严格单调?
func MonoStackTemperature(l []int) []int {
n := len(l)
ans := make([]int, n, n)
// 建立单调栈 增?减
// 怎么选择? :减
mono := make([]int, 1, 1)
for i := 1; i < n; i++ {
e := l[i]
// 元素入栈
m := len(mono)
for ; m > 0; m-- {
if l[mono[m-1]] < e {
// 出栈
// 注意::::这里有重复元素了,不是严格单调了
p := mono[m-1]
ans[p] = i - p
mono = mono[0 : m-1]
} else {
break
}
}
mono = append(mono, i)
}
return ans
}
{name: "1", args: args{l: []int{2, 3, 1}}, want: []int{1, 0, 0}},
{name: "2", args: args{l: []int{2, 5, 6, 3}}, want: []int{1, 1, 0, 0}},
{name: "3", args: args{l: []int{2, 6, 5, 3}}, want: []int{1, 0, 0, 0}},
{name: "4", args: args{l: []int{3, 2, 4}}, want: []int{2, 1, 0}},
{name: "5", args: args{l: []int{8, 9, 3, 2, 4}}, want: []int{1, 0, 2, 1, 0}},
{name: "6", args: args{l: []int{1, 2, 3}}, want: []int{1, 1, 0}},
{name: "7", args: args{l: []int{2, 2, 3}}, want: []int{2, 1, 0}},
{name: "8", args: args{l: []int{2, 2, 1}}, want: []int{0, 0, 0}},
{name: "9", args: args{l: []int{1, 2, 2, 3}}, want: []int{1, 2, 1, 0}},
https://leetcode.cn/problems/next-greater-element-i/solution/xia-yi-ge-geng-da-yuan-su-i-by-leetcode-bfcoj/
https://leetcode.cn/problems/132-pattern/
https://leetcode.cn/problems/daily-temperatures/
https://leetcode.cn/problems/0ynMMM/
https://liuzhenglaichn.gitbook.io/algorithm/monotonic-stack
【西法带你学算法】单调栈解题模板秒杀八道题 https://mp.weixin.qq.com/s/Mb8PAxMj2KLTQ1QrCh8XAA
数据结构-单调栈 https://mp.weixin.qq.com/s/gPv3rndt9wAnglltvfeblw
什么是单调栈
单调栈顾名思义就是满足一定单调性的栈,但是由于栈的特性,单调栈中的元素只能在单调栈的一端进出。
在加入新元素时,如果栈顶元素小于(或大于)新元素,就直接加入,否则不断弹出栈顶元素直到栈顶元素小于(或大于)新元素,这样就能保证栈的单调性。
从一道题说起
LeetCode-84:给定n个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为1。求在该柱状图中,能够勾勒出来的矩形的最大面积。
那么如何思考这道题呢?😕
假设我们有6根柱子,高度分别为114514。注意到,我们找到的矩形一定有一个起始柱子和一个终止柱子,我们的矩形就是在这两个柱子之间找到的。并且最大矩形的高,一定是某一个柱子的高,这个可以用反证法很容易得到。
有了这些,我们来考虑一下以某一个柱子的高度为基准的情况。
假设我们以第三根柱子(高度为4)为基准,我们要得到的起始柱子和终止柱子,其实就是以这根柱子为基准向左右扩展得到的左边界和右边界。什么样的柱子能够作为左右边界呢?显然,高度大于或等于基准柱子是基本要求,并且起始柱子和终止柱子之间的所有柱子也都应该要保证这一点。而在基准高度相等的情况下,自然是柱子越多越好,分析到这里,我们就可以把问题转换成找到基准柱子向左右方向第一根高度小于基准柱子的柱子,在这个例子中,起始柱子和终止柱子分别是第3和第4根柱子。现在,就可以利用单调栈求解了。😏
如果我们把柱子按顺序放入栈中,会发生什么?我们很容易得到这样的不变式:新加入的元素,一定是栈顶要弹出的元素向右数,第一个小于栈顶元素的元素,栈中第二个元素,一定是栈顶元素向左数,第一个小于栈顶元素的元素。下面分析例子中的情况:
-
• 首先是第1根柱子,高度为1,此时栈为空,压入。
-
• 第2根柱子高度与第1根柱子相等,弹出第1根,栈为空,压入。
-
• 第3根柱子比第2根柱子大,压入,此时栈中有第2根柱子和第3根柱子。
-
• 第4根柱子比第3根柱子大,压入,此时栈中有第2根柱子、第3根柱子和第4根柱子。
-
• 第5根柱子比第4根柱子小,弹出第4根柱子,弹出的时候分析第4根柱子,这时候显然第4根柱子的终止柱子是第4根柱子,也就是
5-1=4,因为新加入的元素是向右第一个小于栈顶元素的元素。而起始柱子呢?其实就是弹出栈顶元素后的栈顶元素的位置加上1,也就是3+1=4,那么很容易得到,以第4根柱子为基准的矩形最大是(4-4+1)*4=4。 -
• 重复这个过程。
最后在所有的元素都完成入栈了以后,可以对剩下没有出栈的元素进行出栈操作。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号