内存空间有限情况下的词频统计 Trie树 前缀树
数据结构与算法专题——第十二题 Trie树
https://mp.weixin.qq.com/s/nndr2AcECuUatXrxd3MgCg
今天来聊一聊Trie树,Trie树的名字有很多,比如字典树,前缀树等等。
一:概念
下面有and,as,at,cn,com这几个关键词,构建成 trie 树如下。
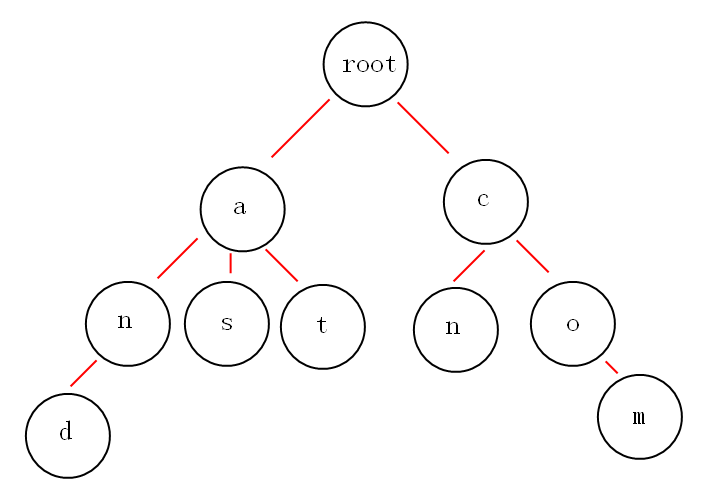
从上面图中,应该可以或多或少的发现一些好玩的特性。
- 根节点不包含字符,除根节点外的每一个子节点都包含一个字符。
- 从根节点到某一节点,路径上经过的字符连接起来,就是该节点对应的字符串。
- 每个单词的公共前缀作为一个字符节点保存。
二:使用范围
既然学Trie树,肯定要知道这玩意是用来干嘛的?
1. 词频统计。
可能有人要说了,词频统计简单啊,一个hash或者一个堆就可以打完收工,但问题来了,如果内存有限呢?还能这么玩吗?这种限制级条件下就可以用trie树来压缩下空间,因为公共前缀都是用一个节点保存的。
2. 前缀匹配
就拿上面的图来说吧,如果我想获取所有以 "a" 开头的字符串,从图中可以很明显的看到是:and,as,at,如果不用trie树,你该怎么做呢?很显然朴素的做法时间复杂度为O(N2) ,用Trie树就不一样了,它可以做到h,h为你检索单词的长度,可以说这是秒杀的效果。
举个例子:现有一个编号为1的字符串”and“,怎样插入到trie树中呢?采用动态规划的思想,将编号”1“计入到每个途径的节点中,那么以后我们要找”a“,”an“,”and"为前缀的字符串的编号将会轻而易举。
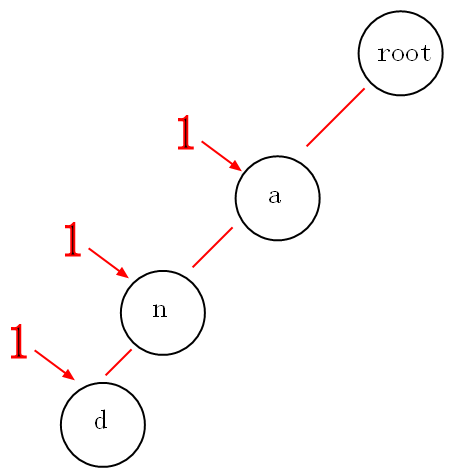
三:实际操作
到现在为止,我想大家已经对trie树有了大概的掌握,下面看看如何来实现。
1:定义trie树节点
为了方便,我也采用纯英文字母,大家都知道字母有26个,所以构建的trie树就是一个26叉树,每个节点包含26个子节点,实现代码如下:
/// <summary>
/// Trie树节点
/// </summary>
public class TrieNode
{
/// <summary>
/// 26个字符,也就是26叉树
/// </summary>
public TrieNode[] childNodes;
/// <summary>
/// 词频统计
/// </summary>
public int freq;
/// <summary>
/// 记录该节点的字符
/// </summary>
public char nodeChar;
/// <summary>
/// 插入记录时的编码id
/// </summary>
public HashSet<int> hashSet = new HashSet<int>();
/// <summary>
/// 初始化
/// </summary>
public TrieNode()
{
childNodes = new TrieNode[26];
freq = 0;
}
}
2: 添加操作
从上面图中,应该可以或多或少的发现一些好玩的特性。
- 根节点不包含字符,除根节点外的每一个子节点都包含一个字符。
- 从根节点到某一节点,路径上经过的字符连接起来,就是该节点对应的字符串。
- 每个单词的公共前缀作为一个字符节点保存。
二:使用范围
既然学Trie树,肯定要知道这玩意是用来干嘛的?
1. 词频统计。
可能有人要说了,词频统计简单啊,一个hash或者一个堆就可以打完收工,但问题来了,如果内存有限呢?还能这么玩吗?这种限制级条件下就可以用trie树来压缩下空间,因为公共前缀都是用一个节点保存的。
2. 前缀匹配
就拿上面的图来说吧,如果我想获取所有以 "a" 开头的字符串,从图中可以很明显的看到是:and,as,at,如果不用trie树,你该怎么做呢?很显然朴素的做法时间复杂度为O(N2) ,用Trie树就不一样了,它可以做到h,h为你检索单词的长度,可以说这是秒杀的效果。
举个例子:现有一个编号为1的字符串”and“,怎样插入到trie树中呢?采用动态规划的思想,将编号”1“计入到每个途径的节点中,那么以后我们要找”a“,”an“,”and"为前缀的字符串的编号将会轻而易举。



