DP 状态 DP 转移方程 动态规划解题思路
练习：
力扣 https://leetcode.cn/problems/partition-equal-subset-sum/solution/fen-ge-deng-he-zi-ji-by-leetcode-solution/
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。
实践：
1、动态规划，在确定状态转移逻辑后，要注意边界条件的正确性，例：
斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：
F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给定 n ，请计算 F(n) 。
func fib(n int) int {
if n <= 1 {
return n
}
a, b, c := 0, 1, 0
for i := 1; i < n; i++ {
c = a + b
a = b
b = c
}
return c
}
链接：https://leetcode.cn/problems/fibonacci-number
注意：可能可以将状态转移表达的逻辑转化为递归表达
func fib(n int) int {
if n <= 1 {
return n
}
return fib(n-1) + fib(n-2)
}
递推关系 和 状态转移 可能可以互相转化、是等价的
区别：
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
https://leetcode.cn/problems/climbing-stairs/
正确
func climbStairs(n int) int {
a, b, c := 0, 0, 1
for i := 1; i <= n; i++ {
a = b
b = c
c = a + b
}
return c
}
错误
func fib(n int) int {
a, b, c := 0, 0, 1
for i := 1; i <= n; i++ {
a = b
b = c
c = a + b
}
return c
}
func maxSubArray(nums []int) int {
n := len(nums) // >0
dp := nums[0]
ans := dp
for i := 1; i < n; i++ {
if dp > ans {
ans = dp
}
if dp > 0 {
dp += nums[i]
} else {
dp = nums[i]
}
}
if dp > ans {
ans = dp
}
return ans
}
https://docs.python.org/3.7/library/functools.html
Example of efficiently computing Fibonacci numbers using a cache to implement a dynamic programming technique:
@lru_cache(maxsize=None)
def fib(n):
if n < 2:
return n
return fib(n-1) + fib(n-2)
>>> [fib(n) for n in range(16)]
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610]
>>> fib.cache_info()
CacheInfo(hits=28, misses=16, maxsize=None, currsize=16)
New in version 3.2.
Changed in version 3.3: Added the typed option.
https://en.wikipedia.org/wiki/Dynamic_programming
https://zh.wikipedia.org/wiki/动态规划
动态规划（英语：Dynamic programming，简称DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划常常适用于有重叠子问题[1]和最优子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。
动态规划背后的基本思想非常简单。大致上，若要解一个给定问题，我们需要解其不同部分（即子问题），再根据子问题的解以得出原问题的解。
通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，从而减少计算量：一旦某个给定子问题的解已经算出，则将其记忆化存储，以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。
动态规划在查找有很多重叠子问题的情况的最优解时有效。它将问题重新组合成子问题。为了避免多次解决这些子问题，它们的结果都逐渐被计算并被保存，从简单的问题直到整个问题都被解决。因此，动态规划保存递归时的结果，因而不会在解决同样的问题时花费时间。
动态规划只能应用于有最优子结构的问题。最优子结构的意思是局部最优解能决定全局最优解（对有些问题这个要求并不能完全满足，故有时需要引入一定的近似）。简单地说，问题能够分解成子问题来解决。
- 最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。最优子结构性质为动态规划算法解决问题提供了重要线索。
- 无后效性。即子问题的解一旦确定，就不再改变，不受在这之后、包含它的更大的问题的求解决策影响。
- 子问题重叠性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率。
背包问题
实验代码
import time
def fib(**kwargs):
n = kwargs['n']
if n < 2:
return n
return fib(n=(n - 1)) + fib(n=(n - 2))
def now():
return time.time()
def runtime(f, **kwargs):
s = now()
f(**kwargs)
e = now()
return e - s
import functools
@functools.lru_cache(maxsize=None)
def fib_cache(**kwargs):
n = kwargs['n']
if n < 2:
return n
return fib_cache(n=(n - 1)) + fib_cache(n=(n - 2))
if __name__ == '__main__':
N = [2, 4, 8, 16, 32, 64]
for i in N:
print(i, ':', fib(n=i), ',', fib_cache(n=i), runtime(fib, n=i), ',', runtime(fib_cache, n=i))
2 : 1 , 1 0.0 , 0.0
4 : 3 , 3 0.0 , 0.0
8 : 21 , 21 0.0 , 0.0 1
6 : 987 , 987 0.0009951591491699219 , 0.0
32 : 2178309 , 2178309 1.3061189651489258 , 0.0
算法萌新如何学好动态规划（1） https://mp.weixin.qq.com/s/RqkrgzQsulFc-PHmB3znmA
算法萌新如何学好动态规划（2） https://mp.weixin.qq.com/s/YeebGBcc5dv2fRYQacgCuQ
算法萌新如何学好动态规划（3） https://mp.weixin.qq.com/s/ssLawuRYafAGd9hVyuUJIg
动态规划问题一直是大厂面试时最频繁出现的算法题，主要原因在于此类问题灵活度高，思维难度大，没有很明显的套路做法。
也正是因为这个原因，我们打算出一个「动态规划」系列文章来尝试破解面试中所涉及的动态规划问题。而本文就是这个系列的第一篇文章，主要目的是说明动态规划是什么，动态规划问题应该如何思考？
本文一共分成三个部分，具体内容框架如下所示：
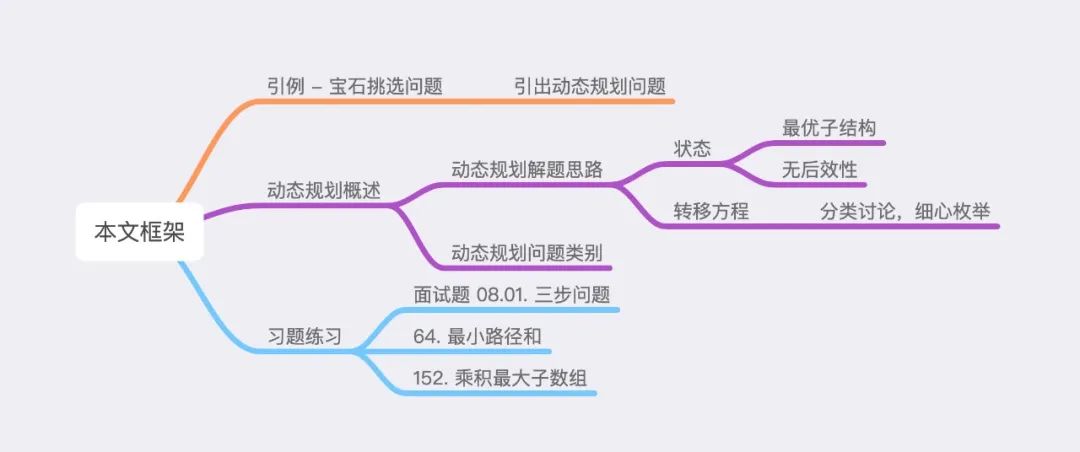
宝石挑选
问题引入
小 Q 是一个宝石爱好者。
这一天，小 Q 来到了宝石古董店，店家觉得小 Q 是个宝石行家，于是决定和小 Q 玩一个游戏。
游戏是这样的，一共有 n 块宝石，每块宝石在小 Q 心中都有其对应的价值。注意，由于某些宝石质量过于差劲，因此存在只有店家倒贴钱，小 Q 才愿意带走的宝石，即价值可以为负数。
小 Q 可以免费带走一个连续区间中的宝石，比如区间 [1,3] 或区间 [2,4] 中的宝石。
请问小 Q 能带走的最大价值是多少？
问题分析
首先思考最暴力的解法。
枚举所有区间，暴力累加区间中宝石的价值，最后选一个价值最大的区间。时间复杂度 O(n^3)。
O(n^3) 显然有些无法接受，因此想想有没有办法优化，比如优化掉暴力累加的部分。
优化 1.0
仔细思考不难发现，我们可以枚举区间右端点，然后固定右端点，左端点不断向左移动，边移动边累加，就可以将时间复杂度优化到 O(n^2)。
例如我们固定右端点是 3，那么左端点就从 3 移动到 1，边移动边累加答案，就可以在移动过程中计算出区间 [3,3]、[2,3]、[1,3] 的答案了。因此枚举所有区间右端点，即可在 O(n^2) 时间复杂度内找到答案。
但是 O(n^2) 时间还是有些过高了，因此思考有没有办法继续优化呢？
优化 2.0
观察 O(n^2) 的解法，不难发现我们用了 O(n) 的时间复杂度才求出了固定某个点为区间右端点时，区间最大价值和。
例如固定了 n 为区间右端点后，我们通过从 n 到 1 枚举左端点，才求出了以 n 为区间右端点时的区间最大价值和，即 O(n) 的时间复杂度。
那么继续思考，「以 n 为区间右端点的区间最大和」，与「以 n - 1 为区间右端点的区间最大和」，这两者是否有关联呢？
为了描述方便，接下来我们用 f[i] 来代替「以 i 为区间右端点的区间最大和」，用 a[i] 来代替第 i 块宝石的价值。
不难发现，如果 f[n - 1] 为正数，则 f[n] 一定等于 f[n - 1] + a[n]；如果 f[n - 1] 为负数，则 f[n] 一定等于 a[n]。因此我们可以推导出如下转移方程：
根据上述转移方程，我们可以在 O(n) 时间复杂度内求出最大的 f[i]，即将此题时间复杂度优化到 O(n)，而这个优化的过程就是「动态规划」的过程。
在上述推导过程中，一共分为两步：
1. 将整个问题划分为一个个子问题，并令 f[i] 为第 i 个子问题的答案
2. 思考大规模的子问题如何从小规模的子问题推导而来，即如何由 f[i - 1] 推出 f[i]
这两个步骤便是「动态规划」解题思路的核心所在，即确定动态规划时的「状态」与「转移方程」。
动态规划概述
动态规划（Dynamic Programming），因此常用 DP 指代动态规划。本块内容我们主要讲解「动态规划解题思路」与「动态规划问题类别」。
动态规划解题思路
动态规划主要分为两个核心部分，一是确定「DP 状态」，二是确定「DP 转移方程」。
DP 状态
「DP 状态」的确定主要有两大原则：
- 最优子结构
- 无后效性
最优子结构
我们仍以「宝石挑选」例题来讲解这两大原则，首先是「最优子结构」。
什么是「最优子结构」？将原有问题化分为一个个子问题，即为子结构。而对于每一个子问题，其最优值均由「更小规模的子问题的最优值」推导而来，即为最优子结构。
因此「DP 状态」设置之前，需要将原有问题划分为一个个子问题，且需要确保子问题的最优值由「更小规模子问题的最优值」推出，此时子问题的最优值即为「DP 状态」的定义。
例如在「宝石挑选」例题中，原有问题是「最大连续区间和」，子问题是「以 i 为右端点的连续区间和」。并且「以 i 为右端点的最大连续区间和」由「以 i - 1 为右端点的最大连续区间和」推出，此时后者即为更小规模的子问题，因此满足「最优子结构」原则。
由此我们才定义 DP 状态 f[i] 表示子问题的最优值，即「以 i 为右端点的最大连续区间和」。
无后效性
而对于「无后效性」，顾名思义，就是我们只关心子问题的最优值，不关心子问题的最优值是怎么得到的。
仍以「宝石挑选」例题为例，我们令 DP 状态 f[i] 表示「以 i 为右端点的最大连续区间和」，我们只关心「以 i 为右端点的区间」这个子问题的最优值，并不关心这个子问题的最优值是从哪个其它子问题转移而来。
即无论 f[i] 所表示区间的左端点是什么，都不会影响后续 f[i + 1] 的取值。影响 f[i + 1] 取值的只有 f[i] 的数值大小。
那怎样的状态定义算「有后效性」呢？
我们对「宝石挑选」例题增加一个限制，即小 Q 只能挑选长度 <= k 的连续区间。此时若我们定义 f[i] 表示「以 i 为右端点的长度 <= k 的最大连续区间和」，则 f[i + 1] 的取值不仅取决于 f[i] 的数值，还取决于 f[i] 是如何得到的。
因为如果 f[i] 取得最优值时区间长度 = k，则 f[i + 1] 不能从 f[i] 转移得到，即 f[i] 的状态定义有后效性。
最后概括一下，「最优子结构」就是「DP 状态最优值由更小规模的 DP 状态最优值推出」，此处 DP 状态即为子问题。而「无后效性」就是「无论 DP 状态是如何得到的，都不会影响后续 DP 状态的取值」。
DP 转移方程
有了「DP 状态」之后，我们只需要用「分类讨论」的思想来枚举所有小状态向大状态转移的可能性即可推出「DP 转移方程」。
我们继续以「宝石挑选」问题为例。
在我们定义「DP 状态」f[i] 之后，我们考虑状态 f[i] 如何从 f[1] ~ f[i - 1] 这些更小规模的状态转移而来。
仔细思考可以发现，由于 f[i] 表示的是连续区间的和，因此其取值只与 f[i - 1] 有关，与 f[1] ~ f[i - 2] 均无关。
我们再进一步思考，f[i] 取值只有两种情况，一是向左延伸，包含 f[i - 1]，二是不向左延伸，仅包含 a[i]，由此我们可以得到下述「DP 转移方程」：
注意，
动态规划问题类别
讲述完 DP 问题的解题思路后，我们来大致列举一下 DP 问题的类别。
DP 问题主要分为两大类，第一大类是 DP 类型，第二大类是 DP 优化方法。
其中在 DP 类型部分，面试中最常考察的就是「线性 DP」，而在优化方法部分，最常见的是「RMQ 优化」，即使用线段树或其它数据结构查询区间最小值，来优化 DP 的转移过程。
习题练习
接下来我们以三道习题为例，来强化一下确定「DP 状态」和「DP 转移方程」的 DP 问题求解思路。
题目描述
三步问题。有个小孩正在上楼梯，楼梯有 n 阶台阶，小孩一次可以上 1 阶、2 阶或 3 阶。实现一种方法，计算小孩有多少种上楼梯的方式。结果可能很大，你需要对结果模 1000000007。
示例 1:
输入：n = 3输出：4说明: 有四种走法
示例 2:
输入：n = 5输出：13
数据范围
n 范围在 [1, 1000000] 之间
解题思路
DP 问题思路主要就是确定「DP 状态」与「DP 转移方程」，因此我们首先考虑「DP 状态」。
「DP 状态」的确定有两大原则，一是「最优子结构」，二是「无后效性」，简要概括就是将原问题划分为多个子问题，且「大规模子问题最优值」仅与「小规模子问题最优值」有关，与「小规模子问题最优值」是如何得到的无关。
此题需要求出爬 n 阶楼梯的总方案数，因此很容易想到子问题是爬 i 阶楼梯的总方案数。接下来再进一步验证该状态是否符合「最优子结构」与「无后效性」两大原则。
令 f[i] 表示爬 i 阶楼梯的总方案数，原问题被划分为了多个求最优值的子问题，继续思考，不难发现小孩爬楼梯只有三种选项，一次上 1、2、3 阶，因此 f[i] 的值仅由 f[i - 1]、f[i - 2]、f[i - 3] 的值决定，因此符合「最优子结构」原则。
再进一步思考，f[i] 的取值与 f[i - 1]、f[i - 2]、f[i - 3] 的数值是如何得到的无关，因此符合「无后效性」原则。
确定完「DP 状态」后，我们再来确定「DP 转移方程」。
由于小孩只有三种爬楼选项，因此 f[i] 的值仅由 f[i - 3] ～ f[i - 1] 决定。且由于爬楼的最后一步不同，因此 f[i] 的值由 f[i - 3] ～ f[i - 1] 累加得到，即如下所示：
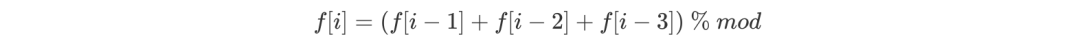
注意，f[1] = 1，且转移时需要注意 f[i - 1]、f[i - 2]、f[i - 3] 不要越界。
C++ 代码实现
class Solution {public:vector<int> f;int mod = 1000000007;int waysToStep(int n) {f.resize(n+1);f[0] = 1;for(int i = 1; i <= n; i++) {f[i] = f[i-1];if(i >= 2) f[i] = (f[i] + f[i-2]) % mod;if(i >= 3) f[i] = (f[i] + f[i-3]) % mod;}return f[n];}};
题目描述
给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。
说明：每次只能向下或者向右移动一步。
示例 1:
输入:[[1,3,1],[[]输出: 7解释: 因为路径 1→3→1→1→1 的总和最小。
解题思路
仍然是相同的解题思路，即依次确定「DP 状态」与「DP 转移方程」，且「DP 状态」的确定需要满足「最优子结构」与「无后效性」。
此题需要求出从左上角出发，到达坐标（m,n）的路径数字和最小值。因此不难想到，子问题就是从左上角出发，到达坐标（i,j）的路径数字和最小值。
令 f[i][j] 表示从左上角到坐标（i,j）的路径数字和最小值，原问题即可被划分为多个求最优值的子问题，且由于每次只能向下或向右移动一步，因此 f[i][j] 的取值由 f[i - 1][j] 和 f[i][j - 1] 的值决定，即符合「最优子结构原则」。
进一步验证，可以发现，f[i][j] 的取值与 f[i - 1][j] 和 f[i][j - 1] 所对应的具体路径无关，因此符合「无后效性」。
此处啰嗦一下。如果题目改为每次可以向上、下、左、右移动一步，且不能走重复的格子，则 f[i][j] 的值虽然与 f[i][j - 1]、f[i][j + 1]、f[i - 1][j]、f[i + 1][j] 的值有关，但由于「不能走重复的格子」这一限制，f[i][j - 1] ～ f[i + 1][j] 所对应的具体路径会影响到 f[i][j] 的取值，即不符合「无后效性」。
确定完「DP 状态」后，继续确定「DP 转移方程」。
由于只能向下或向右移动一步，且由于其最后一步不同，因此 f[i][j] 由 f[i - 1][j] 和 f[i][j - 1] 中的最小值转移得到，即如下所示：
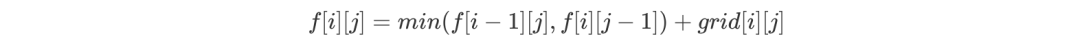
注意，grid[i][j] 表示坐标（i,j）处的数字大小，f[1][1] = grid[1][1] ，转移时需要注意不要越界。
C++ 代码实现
class Solution {public:int minPathSum(vector<vector<int>>& grid) {for(int i = 0; i < grid.size(); i++)for(int j = 0; j < grid[0].size(); j++) {if(i == 0 && j == 0) continue;int tp = 1e9;if(i > 0) tp = min(tp, grid[i-1][j]);if(j > 0) tp = min(tp, grid[i][j-1]);grid[i][j] += tp;}return grid[grid.size()-1][grid[0].size()-1];}};
题目描述
给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。
示例 1:
输入: [2,3,-2,4]输出: 6解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: [-2,0,-1]输出: 0解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
解题思路
继续采用相同的解题思路，即依次确定「DP 状态」与「DP 转移方程」，且「DP 状态」的确定需要满足「最优子结构」与「无后效性」。
此题其实是「宝石挑选」问题的进阶版，即连续区间最大乘积。因此与「宝石挑选」问题的思路一致，令 f[i] 表示以 i 为右端点的连续区间最大乘积，即可将原问题划分为多个求最优值的子问题，但这个状态定义是否符合「最优子结构」原则呢？
我们可以举一个例子来进一步思考。
例如给出 nums = [2,-1,-2]，根据上述 f[i] 的定义，我们可以得到 f = [2,-1,4]。不难发现 
f[i] 的值与 f[i - 1] 的值无关，即 DP 状态最优值无法由更小规模的 DP 状态最优值推出，因此不符合「最优子结构」原则。
于是问题来了，怎样的状态定义才符合「最优子结构」呢？
继续思考可以发现，上述状态定义出错的原因主要在于如果 nums[i] 为负数，则 f[i - 1] * nums[i] 只会越乘越小。因此我们需要根据 nums[i] 的正负值进行分类讨论：
由此可以发现，我们需要引入新的「DP 状态」。令 maxn[i] 表示「以 i 为右端点的连续区间最大乘积」，minn[i] 表示「 以 i 为右端点的连续区间最小乘积」。
不难发现 maxn[i]、minn[i] 的取值由 maxn[i - 1] 、minn[i - 1] 的值推导而来，且与其具体的区间大小无关，因此同时满足「最优子结构」与「无后效性」原则。
最后我们再通过「分类讨论」即可确定如下「DP 转移方程」：
if(nums[i] > 0) {maxn[i] = max(nums[i], maxn[i - 1] * nums[i]);minn[i] = min(nums[i], minn[i - 1] * nums[i]);}else {maxn[i] = max(nums[i], minn[i - 1] * nums[i]);minn[i] = min(nums[i], maxn[i - 1] * nums[i]);}
总结一下，此题根据「最优子结构」原则否定了第一种状态定义。否定之后进一步观察题目性质，得到了新的「DP 状态」，并通过「分类讨论」的方式推出「DP 转移方程」，使得本题得以圆满解决。
C++ 代码实现
class Solution {public:vector<int> maxn, minn;int maxProduct(vector<int>& nums) {int n = nums.size(), ans = nums[0];maxn.resize(n);minn.resize(n);maxn[0] = minn[0] = nums[0];for (int i = 1; i < nums.size(); ++i) {if(nums[i] > 0) {maxn[i] = max(nums[i], maxn[i - 1] * nums[i]);minn[i] = min(nums[i], minn[i - 1] * nums[i]);}else {maxn[i] = max(nums[i], minn[i - 1] * nums[i]);minn[i] = min(nums[i], maxn[i - 1] * nums[i]);}ans = max(ans, maxn[i]);}return ans;}};
总结
最后我们来总结一下 DP 问题的解题思路：
- 确定「DP 状态」
- 符合「最优子结构」原则：DP 状态最优值由更小规模的 DP 状态最优值推出
- 符合「无后效性」原则：状态的得到方式，不会影响后续其它 DP 状态取值
- 确定「DP 转移方程」
- 分类讨论，细心枚举
最后的最后，希望大家在求解 DP 问题时可以参考上述解题思路，祝大家刷题愉快！
BY /
本文作者：Gene_Liu
如何学好动态规划（2） 原创 Gene_Liu LeetCode力扣 今天
算法萌新如何学好动态规划（1） https://mp.weixin.qq.com/s/rhyUb7d8IL8UW1IosoE34g
动态规划概述
动态规划（Dynamic Programming），因此常用 DP 指代动态规划。本块内容我们主要讲解「动态规划解题思路」与「动态规划问题类别」。
动态规划解题思路
动态规划主要分为两个核心部分，一是确定「DP 状态」，二是确定「DP 转移方程」。
DP 状态
「DP 状态」的确定主要有两大原则：
- 最优子结构
- 无后效性
最优子结构
我们仍以「宝石挑选」例题来讲解这两大原则，首先是「最优子结构」。
什么是「最优子结构」？将原有问题化分为一个个子问题，即为子结构。而对于每一个子问题，其最优值均由「更小规模的子问题的最优值」推导而来，即为最优子结构。
因此「DP 状态」设置之前，需要将原有问题划分为一个个子问题，且需要确保子问题的最优值由「更小规模子问题的最优值」推出，此时子问题的最优值即为「DP 状态」的定义。
例如在「宝石挑选」例题中，原有问题是「最大连续区间和」，子问题是「以 i 为右端点的连续区间和」。并且「以 i 为右端点的最大连续区间和」由「以 i - 1 为右端点的最大连续区间和」推出，此时后者即为更小规模的子问题，因此满足「最优子结构」原则。
由此我们才定义 DP 状态 f[i] 表示子问题的最优值，即「以 i 为右端点的最大连续区间和」。
算法萌新如何学好动态规划（2）
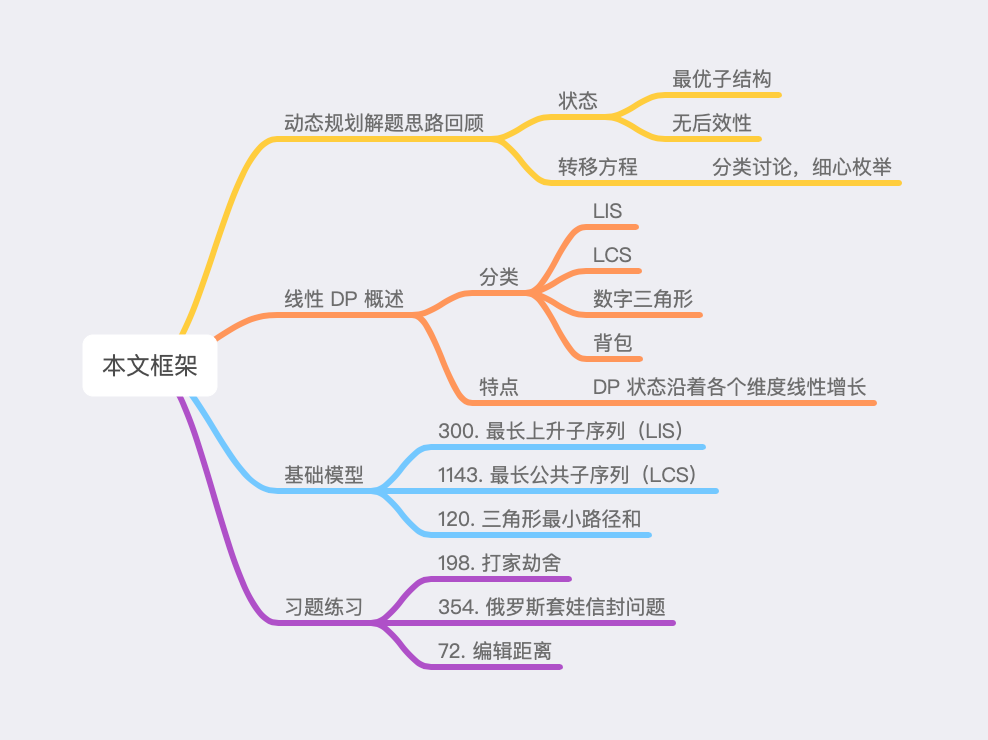
动态规划解题思路回顾
在正式开始线性 DP 的介绍前，我们需要回忆一下「算法萌新如何学好动态规划（一）」中的主要内容，即动态规划的解题思路。
动态规划主要分为两个核心部分，一是确定「DP 状态」，二是确定「DP 转移方程」。「DP 状态」的确定有两大原则，一是「最优子结构」，二是「无后效性」，简要概括就是将原问题划分为多个子问题，且「大规模子问题最优值」仅与「小规模子问题最优值」有关，与「小规模子问题最优值」是如何得到的无关。此处的「大规模」与「小规模」，就是「DP 问题」的关键所在，也是 DP 问题分类的重要标准。确定完「DP 状态」后，只需要分类讨论、细心枚举各种情况，即可得到「DP 转移方程」。大家在做题时，需要仔细体会每道题的「DP 状态」与「DP 转移方程」，认真考虑这两部分是通过怎样的思考得出的，才能不断加深对「动态规划」问题的理解。
线性 DP 概述
线性划分 DP 规模的动态规划算法被统称为线性 DP。在线性 DP 中，DP 状态从「小规模」转移到「大规模」的同时， DP 状态沿着各个维度线性增长。线性 DP 的常见分类如下，其中「最长上升子序列 LIS」、「最长公共子序列 LCS」、「数字三角形」为基础线性 DP 模型，将于本文下一部分介绍，而「背包问题」由于种类繁多，将放到后续系列文章中讲解。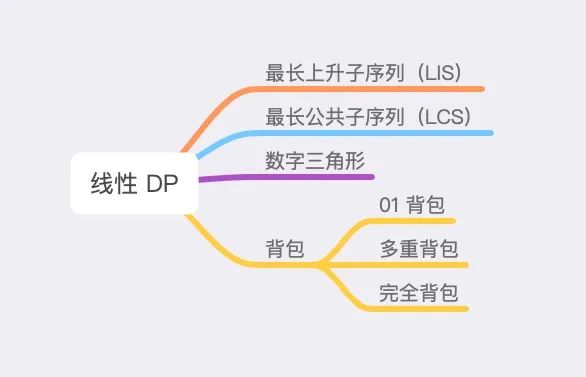
基础模型
熟练掌握「动态规划」问题的基础模型对于后续的习题练习非常重要，因此对于下述的三个模型，大家需要仔细把握其思想，尤其是「DP 状态」的设立思想。300. 最长上升子序列（LIS）
题目描述
给定一个无序的整数数组，找到其中最长上升子序列的长度。
示例
输入: [10,9,2,5,3,7,101,18]输出: 4解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。
模型讲解
求一个无序数组的最长上升子序列，如果是第一次见到这样的问题，那肯定没有什么思路，这个时候我们可以减小长度，从小规模的问题着手思考。如果长度为 1，答案等于多少？很明显，答案也等于 1。那如果长度为 2 呢？那我们需要考虑第二个数是否比第一个数大，如果比第一个数大，则答案为 2，否则为 1。那如果长度为 3 呢？那我们需要枚举第三个数是否比第二个数或第一个数大，如果比它大，则可以直接从第二个数或第一个数的答案直接转移而来。因此我们可以如下制定「DP 状态」，f[i] 表示仅考虑前 i 个数，以第 i 个数为结尾的最长上升子序列的最大长度。由此我们可以推出如下转移方程：
该模型「DP 状态」的关键在于固定了最后一个数字，而这样做的原因在于对于一个最长上升子序列，我们只需要关注它最后一个数字，对于其前面的数字我们并不关心。该模型的时间复杂度为 O(n^2)，其中 n 为数组长度。另外，该模型还可以用二分优化到 O(nlog(n))，大家感兴趣的话可以自行了解。
C++ 代码实现
class Solution {public:int lengthOfLIS(vector<int>& nums) {int sz = nums.size(), ans = 0;vector<int> f(sz, 0);for(int i = 0; i < sz; i++) {int tmp = 1;for(int j = i-1; j >= 0; j--) {if(nums[i] > nums[j])tmp = max(tmp, f[j]+1);}f[i] = tmp;ans = max(ans, tmp);}return ans;}};
1143. 最长公共子序列（LCS）
题目描述
给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。一个字符串的「子序列」是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。若这两个字符串没有公共子序列，则返回 0。示例 1
输入：text1 = "abcde", text2 = "ace"输出：3解释：最长公共子序列是 "ace"，它的长度为 3。
示例 2
输入：text1 = "abc", text2 = "abc"输出：3解释：最长公共子序列是 "abc"，它的长度为 3。
示例 3
输入：text1 = "abc", text2 = "def"输出：0解释：两个字符串没有公共子序列，返回 0。
提示
模型讲解
与 LIS 模型不同的是，最长公共子序列 LCS 涉及到了两个字符数组，不再是基于单数组的问题。根据 LIS 模型「DP 状态」设置的经验，以及「线性 DP」的核心特点，即 DP 状态沿着各个维度线性增长，我们可以如下制定「DP 状态」，f[i][j] 表示第一个串的前 i 个字符与第二个串的前 j 个字符的最长公共子序列长度。该状态的转移方程没有上一个模型这么直接，因此我们需要进行分类讨论。假如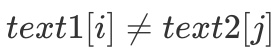
，即 text1[i] 无法与 text2[j] 匹配，因此 f[i][j] = max(f[i][j - 1]，f[i - 1][j])。假如 text1[i] == text2[j]，则 text1[i] 可以与 text2[j] 匹配，因此我们可以增加一种转移方式， f[i][j] = f[i - 1][j - 1] + 1。综合上述情况，我们可以得到最终的「DP 转移方程」：
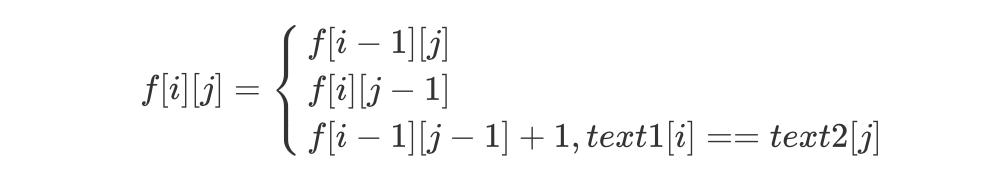
C++ 代码实现
class Solution {public:int longestCommonSubsequence(string text1, string text2) {int n = text1.length(), m = text2.length();vector<vector<int> > f(n+1, vector<int>(m+1, 0));for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {f[i][j] = max(f[i-1][j], f[i][j-1]);if(text1[i-1] == text2[j-1])f[i][j] = max(f[i][j], f[i-1][j-1]+1);}}return f[n][m];}};
120. 三角形最小路径和
题目描述
给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。相邻的结点在这里指的是「下标」与「上一层结点下标」相同或者等于「上一层结点下标 + 1 」的两个结点。例如，给定三角形：[[2],[3,4],[6,5,7],[4,1,8,3]]
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。
说明
如果你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分。模型讲解
该模型即为「线性 DP」基础模型之一：数字三角形，即最常见的二维坐标系「DP 模型」。考虑到「线性 DP」中 DP 状态沿着各个维度线性增长的这一特点，以及本题所求的从上到下的最小路径和，不难得出状态 f[i][j] 表示从顶点出发到达第 i 行第 j 列这个点时的最小路径和。
由于题目中限制（i,j）只能由（i - 1,j - 1）和（i - 1,j）两个点到达，因此我们可以得到如下「DP 转移方程」：
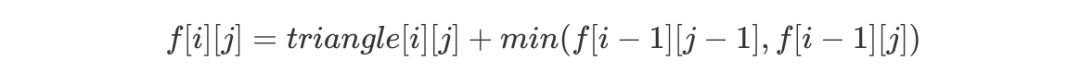
C++ 代码实现
class Solution {public:int minimumTotal(vector<vector<int>>& triangle) {int n = triangle.size(), ans = 1e9;vector<vector<int> > f(n+1, vector<int>(n+1, 0));for(int i = 0; i < n; i++) {for(int j = 0; j < triangle[i].size(); j++) {if(j == triangle[i].size()-1)f[i+1][j+1] = triangle[i][j] + f[i][j];else if(j == 0)f[i+1][j+1] = triangle[i][j] + f[i][j+1];elsef[i+1][j+1] = triangle[i][j] + min(f[i][j+1], f[i][j]);if(i == n-1)ans = min(ans, f[i+1][j+1]);}}return ans;}};
滚动数组优化
上述「DP 转移方程」的时间复杂度为 O(n^2)，空间复杂度也为 O(n^2)，但根据题目中的提示，本题是可以优化至 O(n) 空间复杂度的。这种优化方法称为「滚动数组优化」，在「DP 问题」中非常常见，主要适用于 f[i][j] 仅由 f[i - 1][k] 转移而来的情况。例如在本题中，「DP 转移方程」如下：
不难发现，f[i][j] 仅由 f[i - 1][j - 1] 和 f[i - 1][j] 所决定，因此对于一个固定的 i，我们可以从 n 到 1 倒序枚举 j，由此可以优化至如下转移方程：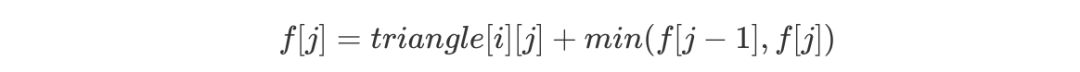
代码形式如下所示：（未进行边界处理，仅作为转移示例）
for(int i = 0; i < n; i++) {for(int j = triangle[i].size()-1; j >= 0; j--) {f[j] = triangle[i][j] + min(f[j-1], f[j]);}}
在上述代码中我们可以发现，在更新 f[j] 时，f[j - 1] 与 f[j] 并未更新，此时的 f[j - 1] 与 f[j] 其实是 f[i - 1][j - 1] 和 f[i - 1][j] 的值，因此这种转移方式正确。
经过滚动数组优化后，该算法的空间复杂度为 O(n) ，时间复杂度不变，仍为 O(n^2)。滚动数组完整代码
class Solution {public:int minimumTotal(vector<vector<int>>& triangle) {int n = triangle.size(), ans = 1e9;vector<int> f(n+1, 0);for(int i = 0; i < n; i++) {for(int j = triangle[i].size()-1; j >= 0; j--) {if(j == triangle[i].size()-1)f[j+1] = triangle[i][j] + f[j];else if(j == 0)f[j+1] = triangle[i][j] + f[j+1];elsef[j+1] = triangle[i][j] + min(f[j+1], f[j]);if(i == n-1)ans = min(ans, f[j+1]);}}return ans;}};
习题练习
了解完三个常见的「线性 DP」模型后，我们来进行适当的习题练习。对于下述习题，大家需要仔细关注三点：-
如何识别这是一道「线性 DP」问题
-
「DP 状态」是如何设置的
-
如何根据「DP 状态」得到「DP 转移方程」
198. 打家劫舍
题目描述
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你「不触动警报装置的情况下」，一夜之内能够偷窃到的最高金额。示例 1
输入：[1,2,3,1]输出：4解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
示例 2
输入：[2,7,9,3,1]输出：12解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示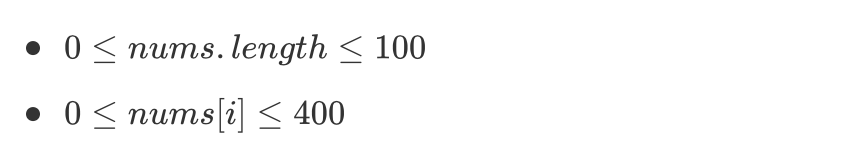
解题思路
首先我们简要概括一下题意，即不能同时偷窃相邻两间房屋，求偷窃的最大金额。不难发现，偷窃的过程是线性增长的，即从左到右，沿街依次偷窃，非常符合「线性 DP」的特征，因此我们可以令 f[i] 表示前 i 间房屋能偷窃到的最高金额，由此得到如下「DP 转移方程」：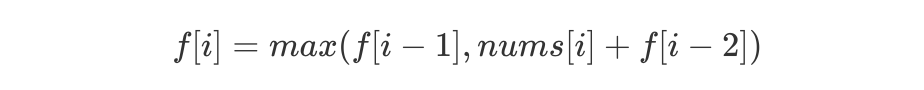
回顾一下之前的最长上升子序列（LIS)，我们令 f[i] 表示以第 i 个数为结尾的最长上升子序列的最大长度，因为最长上升子序列在转移时我们需要知道最后一个数的大小。仿照 LIS 的「DP 状态」，我们也可以令 f[i] 表示前 i 间房屋能偷窃到的最高金额，且第 i 间房屋被偷窃。这样的「DP 状态」也是可以解决本题的，但需要修改「DP 转移方程」，大家可以自行思考并进行尝试。
C++ 代码实现
class Solution {public:int rob(vector<int>& nums) {int n = nums.size();if(n == 0) return 0;vector<int> f(n, 0);for(int i = 0; i < n; i++) {f[i] = nums[i];if(i >= 2) f[i] = max(f[i], f[i-2]+nums[i]);if(i >= 1) f[i] = max(f[i], f[i-1]);}return f[n-1];}};
354. 俄罗斯套娃信封问题
题目描述
给定一些标记了宽度和高度的信封，宽度和高度以整数对形式 (w, h) 出现。当另一个信封的宽度和高度都比这个信封大的时候，这个信封就可以放进另一个信封里，如同俄罗斯套娃一样。请计算最多能有多少个信封能组成一组“俄罗斯套娃”信封（即可以把一个信封放到另一个信封里面）。说明
不允许旋转信封。示例
输入: envelopes = [[5,4],[6,4],[6,7],[2,3]]输出: 3解释: 最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。
解题思路
简要概括题意，求一组二维上升子序列 p1，p2，…，pm，同时满足：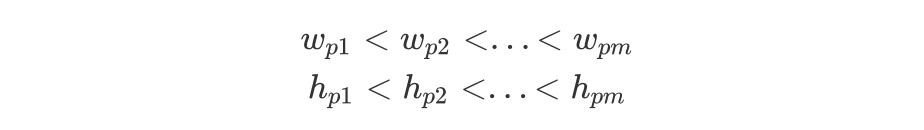
而本题为二维 LIS，若令 f[i][j] 表示以 w = i，h = j 的信封为结尾的最长上升子序列显然不太合适，因此我们需要先控制一维，然后在另一维上进行「DP 转移」。先控制一维，使得「DP 转移」时满足 i < j，则
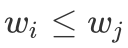，因此我们可以先对于信封进行排序，w 为第一关键字，h 为第二关键字，排完序后再进行初始的一维 LIS「DP 转移」。因此我们排完序后，令 f[i] 表示以第
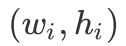为结尾的最长上升子序列，「DP 转移方程」如下：
C++ 代码实现
class Solution {public:int maxEnvelopes(vector<vector<int>>& envelopes) {sort(envelopes.begin(), envelopes.end());int n = envelopes.size(), ans = 0;vector<int> f(n, 0);for(int i = 0; i < n; i++) {int tmp = 0;for(int j = 0; j < i; j++) {if(envelopes[j][1] < envelopes[i][1] && envelopes[j][0] < envelopes[i][0])tmp = max(tmp, f[j]);}f[i] = tmp + 1;ans = max(f[i], ans);}return ans;}};
72. 编辑距离
题目描述
给你两个单词「word1」和「word2」，请你计算出将「word1」转换成「word2」所使用的最少操作数。你可以对一个单词进行如下三种操作：-
插入一个字符
-
删除一个字符
-
替换一个字符
示例 1
输入：word1 = "horse", word2 = "ros"输出：3解释：horse -> rorse (将 'h' 替换为 'r')rorse -> rose (删除 'r')rose -> ros (删除 'e')
示例 2
输入：word1 = "intention", word2 = "execution"输出：5解释：intention -> inention (删除 't')inention -> enention (将 'i' 替换为 'e')enention -> exention (将 'n' 替换为 'x')exention -> exection (将 'n' 替换为 'c')exection -> execution (插入 'u')
解题思路
简要概括题意，使用最少的操作使得「word1」与「word2」相同。很明显所要进行的操作是从左至右线性增长的，不难联想到最长公共子序列（LCS），因此我们令 f[i][j] 表示最少的操作使得「word1」的前 i 个字符与「word2」的前 j 个字符相同。与 LCS 的思考过程一致，假如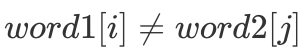 
，则必定涉及删除或增加：
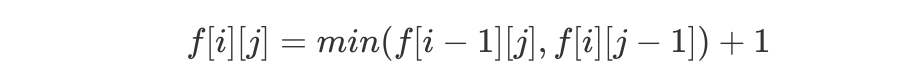
假如 word1[i] == word2[j]，则需要在原先基础上增加一种转移方式：
最后我们需要控制一下边界：
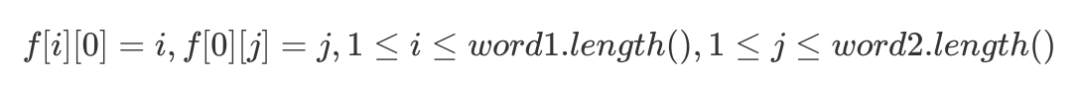
C++ 代码实现
class Solution {public:int minDistance(string word1, string word2) {int n = word1.length(), m = word2.length();vector<vector<int> > f(n+1, vector<int>(m+1, 0));for(int i = 1; i <= n; i++) f[i][0] = i;for(int j = 1; j <= m; j++) f[0][j] = j;for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {if(word1[i-1] == word2[j-1]) f[i][j] = f[i-1][j-1];else f[i][j] = min(f[i-1][j-1]+1, min(f[i][j-1]+1, f[i-1][j]+1));}}return f[n][m];}};
总结
上述习题练习的后两道，「俄罗斯套娃信封问题」与「编辑距离」在力扣上的难度均为困难，但做完题后不难发现其本质仍然是基础线性 DP 模型「LIS」与「LCS」的变形。事实上，大部分「线性 DP」问题（不涉及背包）都可以在最初介绍的三个基础模型「LIS」、「LCS」、「数字三角形」中找到类似的解题思路，因此大家需要熟练掌握。为了方便大家后续查阅，我们将三个模型总结如下：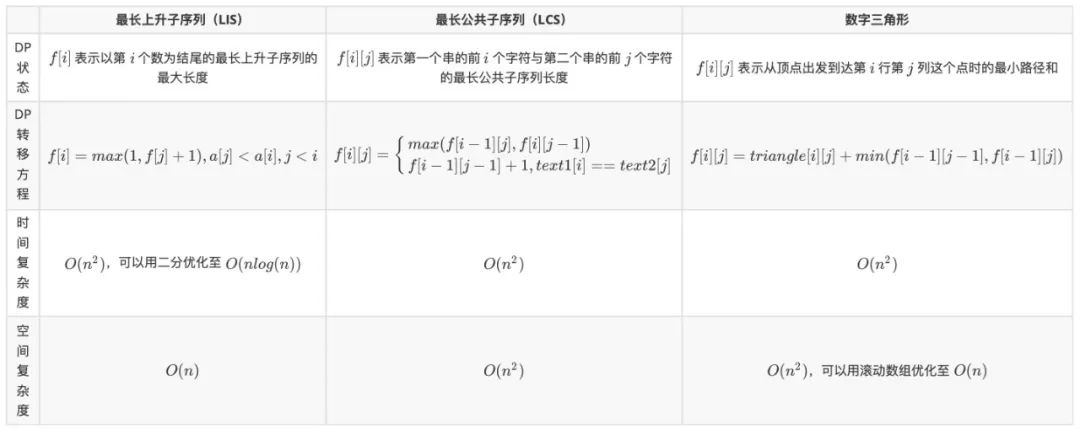
BY /
本文作者：Gene_Liu
算法萌新如何学好动态规划（3）
前文回顾
解题思路回顾
回顾动态规划系列的第一篇文章，动态规划解题过程一共分为两步，一是确定「DP 状态」，二是确定「DP 转移方程」。大家在看本文时，一定要细心体会每一个经典背包模型的「DP 状态」与「DP 转移方程」，认真思考每一个模型中这两部分是如何得到的。学习不同经典模型，理解模型本质，才能不断加深对「动态规划」问题的理解。「DP 状态」的确定有两大原则，一是「最优子结构」，二是「无后效性」，简要概括就是将原问题划分为多个子问题，且「大规模子问题最优值」仅与「小规模子问题最优值」有关，与「小规模子问题最优值」是如何得到的无关。
此处的「大规模」与「小规模」，就是「DP 问题」的关键所在，也是 DP 问题分类的重要标准。
确定完「DP 状态」后，只需要分类讨论、细心枚举各种情况，即可得到「DP 转移方程」。
线性 DP 特点回顾
我们在动态规划系列的第二篇文章中介绍了三个常见的线性 DP 模型，分别是「最长上升子序列 LIS」、「最长公共子序列 LCS」以及「数字三角形」，其特点如下图所示。线性划分 DP 规模的动态规划算法被统称为线性 DP。在线性 DP 中，DP 状态从「小规模」转移到「大规模」的同时，DP 状态沿着各个维度线性增长。
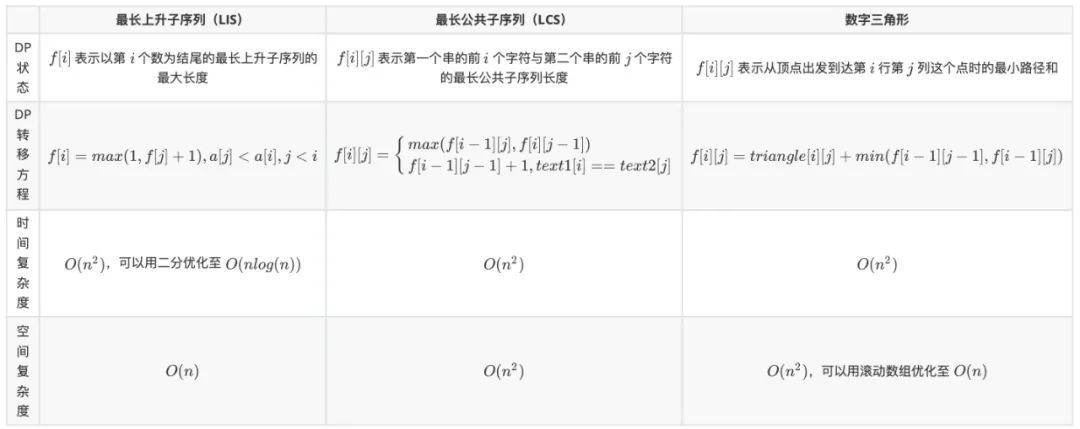本文将介绍第四个线性 DP 模型，即「背包问题」。由于背包问题也是线性 DP 问题，因此也符合线性 DP 的特点，即 DP 状态沿着各个维度线性增长，大家可以在下文中着重关注一下这一特点。
背包问题概述
常见的背包问题一共有三类，分别是「0/1 背包」、「完全背包」以及「多重背包」，接下来我们将依次进行介绍。0/1 背包
0/1 背包的基本模型如下所示：一共有 N 个物品，其中第 i 个物品的体积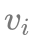为
，价值为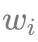 
。现要求选择一些物品放入一个容积为 M 的背包中，使得物品总体积不超过 M 的前提下，物品总价值最大。现在我们来思考下如何根据线性 DP 的知识来解决这个问题。线性 DP 的特点是 DP 状态沿着各个维度线性增长。而本问题中只有三个参数，分别是物品编号、物品体积以及物品价值。由于我们要求的是物品总价值最大，因此不难想到令 DP 状态为 
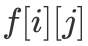，表示仅考虑前 i 个物品，所选物品总体积为 j 时的最大物品总价值。确定「DP 状态」后，我们来考虑「DP 转移方程」是什么。对于第 i 个物品来说，它只有两种状态，即要么取，要么不取。如果不取第 i 个物品，则 
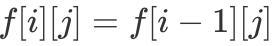；如果取第 i 个物品，则 
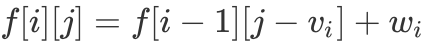，因此我们得到如下「DP 转移方程」：
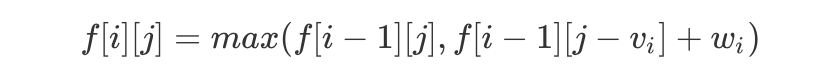其中初值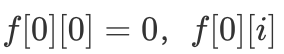 
为负无穷，其中 
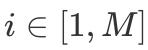，最终答案为 
，代码如下所示。
观察上述代码，不难发现，int DP() {for(int i = 1; i <= M; i++)f[0][j] = -inf; // 负无穷，inf 可以为 1e8f[0][0] = 0;for(int i = 1; i <= N; i++)for(int j = 0; j <= M; j++)if(j >= v[i])f[i][j] = max(f[i-1][j], f[i-1][j-v[i]] + w[i]);elsef[i][j] = f[i-1][j];int ans = 0;for(int i = 0; i <= M; i++)ans = max(ans, f[N][i]);return ans;}
仅由 
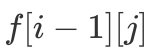和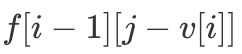 
决定。这就给了我们一个思考角度，即能否将二维数组 f 的第一维去掉？答案显然是可以的，我们可以倒序枚举 j，使得更新 
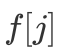时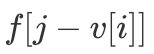
还未被更新，即 
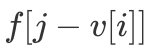代表的实际是 
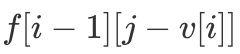的值。这样说可能不好理解，我们先看一下优化后的代码：
根据上述代码，我们不难发现在第 i 轮，更新到int DP() {for(int i = 1; i <= M; i++)f[j] = -inf; // 负无穷，inf 可以为 1e8f[0] = 0;for(int i = 1; i <= N; i++)for(int j = M; j >= v[i]; j--)f[j] = max(f[j], f[j-v[i]] + w[i]);int ans = 0;for(int i = 0; i <= M; i++)ans = max(ans, f[i]);return ans;}
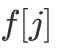时，
与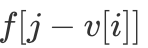 
代表的都是第 i - 1 轮的值，即 
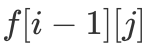与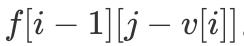 
。而在我们更新完 
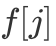后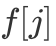， 的值即变为 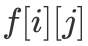的值，由此我们大大降低了该算法的空间开销，这种空间优化方法叫做「滚动数组」。
完全背包
了解完「0/1 背包」模型后，我们继续介绍「完全背包」模型，其基本问题如下所示：一共有 N 类物品，其中第 i 类物品的体积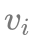为，价值为 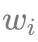，且每类物品可以选无数个。现要求选择一些物品放入一个容积为 M 的背包中，使得物品总体积不超过 M 的前提下，物品总价值最大。不难发现，「完全背包」与「0/1 背包」最大的差别就在于每一类物品可以选多少个，其中「完全背包」每一类物品可以选无数个，而「0/1 背包」中每一类物品只能选 1 个。了解完模型差异后，我们继续思考如何解决该问题。与「0/1 背包」模型比较类似，本问题也只有三个参数，分别是物品编号、物品体积以及物品价值。因此我们可以照搬「0/1 背包」的「DP 状态」，即 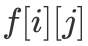表示仅考虑前 i 类物品，所选物品总体积为 j 时的最大物品总价值。由于每一类物品可以选无数次，因此对于 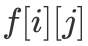来说，如果不取则 
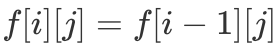，如果取一个则 
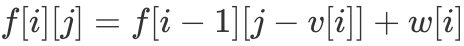，如果取两个则 
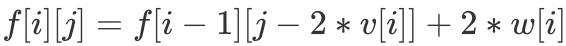，如果取 x 个则 
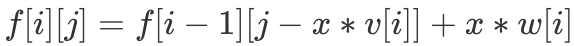。因此我们可以得到
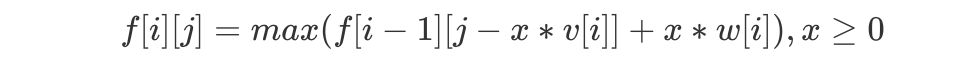但这样的话我们就需要不断遍历 x，显然会导致时间复杂度过高，因此我们还可以继续优化。
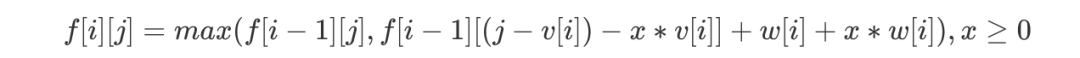又因为 
因此只要正序遍历 j，即保证求取 时，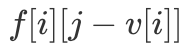
已经得到，「DP 转移方程」就可以优化为
对比「0/1 背包」中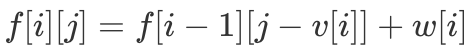 
，「完全背包」由于每类物品可以取多次，因此转移方程变为 
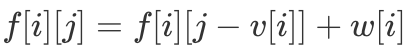，具体代码如下所示。
根据之前介绍的「滚动数组」方法，我们可以将上述代码优化为：int DP() {for(int i = 1; i <= M; i++)f[0][j] = -inf; // 负无穷，inf 可以为 1e8f[0][0] = 0;for(int i = 1; i <= N; i++)for(int j = 0; j <= M; j++)if(j >= v[i])f[i][j] = max(f[i-1][j], f[i][j-v[i]] + w[i]);elsef[i][j] = f[i-1][j];int ans = 0;for(int i = 0; i <= M; i++)ans = max(ans, f[N][i]);return ans;}
int DP() {for(int i = 1; i <= M; i++)f[j] = -inf; // 负无穷，inf 可以为 1e8f[0] = 0;for(int i = 1; i <= N; i++)for(int j = v[i]; j <= M; j++)f[j] = max(f[j], f[j-v[i]] + w[i]);int ans = 0;for(int i = 0; i <= M; i++)ans = max(ans, f[i]);return ans;}
多重背包
最后我们来介绍「多重背包」模型，其基本问题如下所示：一共有 N 类物品，其中第 i 类物品的体积为
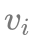，价值为 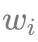，且每类物品只有 
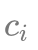个
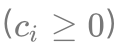。现要求选择一些物品放入一个容积为 M 的背包中，使得物品总体积不超过 M 的前提下，物品总价值最大。将该问题与「0/1 背包」模型进行对比，可以发现唯一差别在于「0/1 背包」中每一类物品的
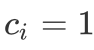，因此我们可以考虑如何将「多重背包」转换为「0/1 背包」进行求解。首先比较容易想到的是，我们可以进行暴力拆分，即将每一类物品拆分为 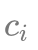个，总物品数量从 N 变为 
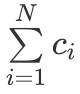，因此我们可以直接使用「0/1 背包」模型进行解决，具体代码如下所示：
直接暴力拆分使得该问题变得简单，但是时间复杂度却显著增加，为int DP() {for(int i = 1; i <= M; i++)f[j] = -inf; // 负无穷，inf 可以为 1e8f[0] = 0;for(int i = 1; i <= N; i++)for(int k = 1; k <= c[i]; k++)for(int j = M; j >= v[i]; j++)f[j] = max(f[j], f[j-v[i]] + w[i]);int ans = 0;for(int i = 0; i <= M; i++)ans = max(ans, f[i]);return ans;}
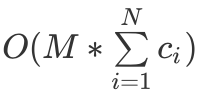。于是我们需要思考有没有什么方法可以对该问题进行优化？答案显然是有的，即对每一类物品进行二进制拆分。首先回顾计算机中二进制的知识，即从 
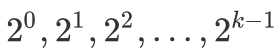这 k 个数字中选取若干个相加，可以表示出 
中的任何整数。因此对于第 i 类物品，其个数为 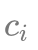，我们可以求出满足 
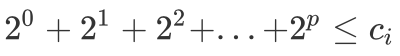的最大的 p，并令 
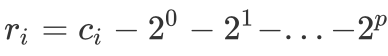。因为 p 是最大的，所以 
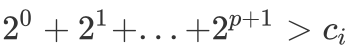，即 
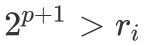。又因为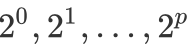 
的最大表示范围为 
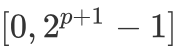，因此我们可以从 
中选取若干个数表示出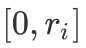 
中的任何整数。又因为 
，因此我们可以使用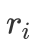 
以及 
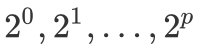表示出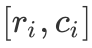 
中的任何整数。所以 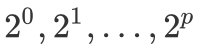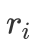，的表示范围恰好为
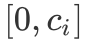，即我们可以将数量为 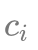的第 i 类物品拆分为 p + 2 个物品，其体积分别为：
其价值分别为：
拆分完每一类物品后，我们再使用「0/1 背包」模型即可求出答案，总时间复杂度为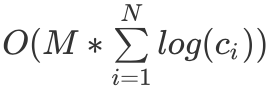 
。
背包问题特点
至此我们介绍完了三大常见的背包模型，分别是「0/1 背包」、「完全背包」、「多重背包」，其区别仅仅在于每一类物品可以选多少个。其中「0/1 背包」是每一类物品只能选一个，「完全背包」则是每一类物品可以选无数个，而「多重背包」则是第 i 类物品最多可以选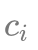个。因此我们可以归纳「背包问题」的特点：有 N 类物品，每类物品可以选 1 个、无数个或 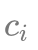个，问是否存在一种选取方案，使其满足某种条件。或者是否存在一种选取方案，使其满足某种条件的同时，得到某种参数的最值。这样归纳可能还是过于抽象，因此我们将在下文「习题练习」中讲解一些具体的题型来帮助大家理解。
习题练习
416. 分割等和子集
题目描述
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。示例 1
输入: [1, 5, 11, 5]输出: true解释: 数组可以分割成 [1, 5, 5] 和 [11].
示例 2
输入: [1, 2, 3, 5]输出: false解释: 数组不能分割成两个元素和相等的子集.
提示
- 每个数组中的元素不会超过 100
- 数组的大小不会超过 200
解题思路
「将数组分割成两个子集，使得两个子集的元素和相等」，假设数组元素个数为N，元素和为 M，则问题可以转化为「现有 N 个数字，是否可以选取若干个数字，使其和为 M/2」。进行这一步转换之后，则可以较为明显的看出该问题本质上是从 N 物品中选取若干个物品，即「背包问题」。并且每个物品只能选一次，因此是「0/1 背包」模型。仿照「0/1 背包」模型，我们可以定义
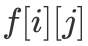为仅考虑前 i 个物品，是否存在一种选择方案使其数值和为 j。我们规定若 
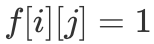则表示存在一种方案；若 
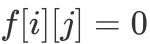则表示不存在可行方案。因此我们可以得到如下「DP 转移方程」：
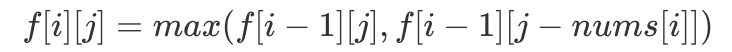定义一下初始条件，
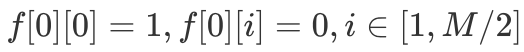。接下来直接套用「0/1 背包」滚动数组版本的代码即可完成本题，具体细节见下述代码。
C++ 代码实现
class Solution {public:vector<int> f;bool canPartition(vector<int>& nums) {// 确保元素和为偶数int sum = 0;for(int item:nums) sum += item;if(sum % 2 != 0) return 0;sum /= 2;// 开辟存储空间f.resize(sum+1);f[0] = 1;// DP 过程for(int i = 1; i <= nums.size(); i++)for(int j = sum; j >= nums[i-1]; j--)if(f[j-nums[i-1]] == 1)f[j] = 1;if(f[sum]) return 1;else return 0;}};
494. 目标和
题目描述
给定一个非负整数数组，
和一个目标数，S。现在你有两个符号 + 和 -。对于数组中的任意一个整数，你都可以从 + 或 - 中选择一个符号添加在前面。返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
示例
输入：nums: [1, 1, 1, 1, 1], S: 3输出：5解释：-1+1+1+1+1 = 3+1-1+1+1+1 = 3+1+1-1+1+1 = 3+1+1+1-1+1 = 3+1+1+1+1-1 = 3一共有5种方法让最终目标和为3。
提示
- 数组非空，且长度不会超过 20 。
- 初始的数组的和不会超过 1000 。
- 保证返回的最终结果能被 32 位整数存下。
解题思路
假设整个数组元素和为 sum，且开头符号为 + 的数字和为 a，则整个开头符号为 - 的数字和为 sum - a。因此若要使数组和为 S，则 a - (sum - a) = S，即 2*a = S + sum。因此问题转变为从 N 个数中选取若干个数，使其总和为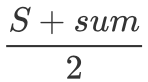
，问有多少种选数方案。由于每个数只能选一次，因此我们可以较为容易地将该问题转化为「0/1 背包」模型。仿照「0/1 背包」，定义 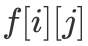表示仅考虑前 i 个数，有多少种选数方案使其数字和为 j。因此我们可以得到如下「DP 转移方程」：
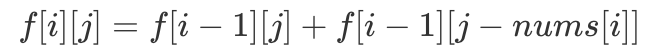定义一下初始条件，
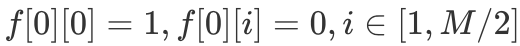。接下来直接套用「0/1 背包」滚动数组版本的代码即可，具体细节见下述代码。
C++ 代码实现
class Solution {public:vector<int> f;int findTargetSumWays(vector<int>& nums, int S) {// 预处理int sum = 0, a = 0;for(int item:nums) sum += item;if(S < -sum || S > sum || (sum + S) % 2) return 0;a = (S + sum) / 2;f.resize(a + 1);// DP 过程f[0] = 1;for(int i = 0; i < nums.size(); i++)for(int j = a; j >= nums[i]; j--)f[j] += f[j-nums[i]];return f[a];}};
322. 零钱兑换
题目描述
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 - 1。示例 1
输入: coins = [1, 2, 5], amount = 11输出: 3解释: 11 = 5 + 5 + 1
示例 2
输入: coins = [2], amount = 3输出: -1
提示
- 你可以认为每种硬币的数量是无限的。
解题思路
从 N 类硬币中选取若干个，使得选取硬币的总金额为 M，求最少所需的硬币个数。很明显这是一道「背包类」问题，且由于每一类硬币可以选取无限个，因此这是一道「完全背包」问题。仿照「完全背包」的思路，定义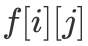表示仅考虑前 i 类硬币，其总金额为 j 时最少所需硬币个数。因此我们可以得到如下「DP 转移方程」：
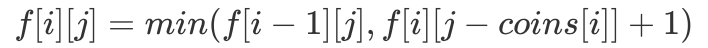定义一下初始条件，
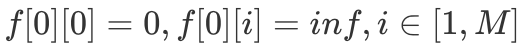。接下来直接套用「完全背包」滚动数组版本的代码即可，具体细节见下述代码。
C++ 代码实现
class Solution {public:vector<int> f;const int inf = 1e8;int coinChange(vector<int>& coins, int amount) {f.resize(amount + 1, inf);f[0] = 0;for(int i = 0; i < coins.size(); i++)for(int j = coins[i]; j <= amount; j++)f[j] = min(f[j], f[j-coins[i]] + 1);if(f[amount] == inf) return -1;else return f[amount];}};
518. 零钱兑换 II
题目描述
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。示例 1
5=55=2+2+15=2+1+1+15=1+1+1+1+1
示例 2
输入: amount = 3, coins = [2]输出: 0解释: 只用面额2的硬币不能凑成总金额3。
示例 3
输入: amount = 10, coins = [10]输出: 1
提示
解题思路
本题与上一题唯一的区别在于，上一题要求的「凑成总金额最少需要的硬币个数」，而本题求的是「凑成总金额的方案数」。因此只需稍微改动一下「DP 状态意义」以及「DP 转移方程」即可。由于本题的硬币依然可以无限取，因此仍然使用「完全背包」模型进行求解。定义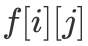 表示仅考虑前 i 类硬币，其总金额为 j 时的组合数。因此可以得到如下「DP 转移方程」：
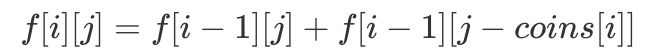初始条件为，
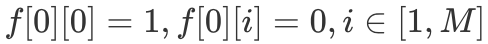。接下来使用「完全背包」滚动数组版本的代码即可，具体细节如下。
C++ 代码实现
class Solution {public:vector<int> f;int change(int amount, vector<int>& coins) {f.resize(amount + 1);f[0] = 1;for(int i = 0; i < coins.size(); i++)for(int j = coins[i]; j <= amount; j++)f[j] += f[j-coins[i]];return f[amount];}};
474. 一和零
题目描述
在计算机界中，我们总是追求用有限的资源获取最大的收益。现在，假设你分别支配着 m 个 0 和 n 个 1。另外，还有一个仅包含 0 和 1 字符串的数组。你的任务是使用给定的 m 个 0 和 n 个 1 ，找到能拼出存在于数组中的字符串的最大数量。每个 0 和 1 至多被使用一次。示例 1
输入: Array = {"10", "0001", "111001", "1", "0"}, m = 5, n = 3输出: 4解释: 总共 4 个字符串可以通过 5 个 0 和 3 个 1 拼出，即 "10","0001","1","0"。
示例 2
输入: Array = {"10", "0", "1"}, m = 1, n = 1输出: 2解释: 你可以拼出 "10"，但之后就没有剩余数字了。更好的选择是拼出 "0" 和 "1"。
提示
- 给定 0 和 1 的数量都不会超过 100。
- 给定字符串数组的长度不会超过 600。
解题思路
简要概括一下题意，一共有 m 个 0，n 个 1。现有 n 个字符串，其中第 i 个字符串需要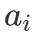
个 0，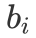
个 1，现问最多可以拼出多少个字符串。这个题看似可能和背包没太大关系，但仔细思考之后，还是可以发现此题的本质仍然是选取若干个字符串，使其 0 和 1 的个数之和分别小于等于 m 和 n，因此仍然是一道背包问题。并且由于每一个字符串只能选一次，因此是一道「0/1 背包」问题。我们仿照「0/1 背包」的思路，定义 
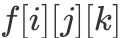表示对于前 i 个字符串，一共有 j 个 0 和 k 个 1 时，能拼出的最大字符串个数。可以发现对比「0/1 背包」的基础模型，我们将「DP 状态」从二维扩展到了三维，主要原因在于本题有两个参数，分别是 0 和 1 的个数。可以理解为有两个背包，要装两种东西，但本质不变，只需在原先基础上扩展一维即可。因此我们可以仿照原先的基础模型，得到如下「DP 转移方程」：
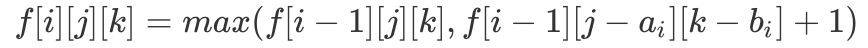初始条件为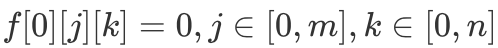 
。由于本题只是在「0/1 背包」模型基础上扩展了一维，因此我们仍然可以使用「滚动数组」的方法将三维空间降低至二维空间，具体代码如下所示。
C++ 代码实现
class Solution {public:vector<vector<int> > f;int findMaxForm(vector<string>& strs, int m, int n) {f.resize(m+1);for(int i = 0; i <= m; i++)f[i].resize(n+1);for(int i = 0; i < strs.size(); i++) {int a = 0, b = 0;for(char c:strs[i]) {if(c == '0') a++;else b++;}for(int j = m; j >= a; j--)for(int k = n; k >= b; k--)f[j][k] = max(f[j][k], f[j-a][k-b] + 1);}return f[m][n];}};
总结
讲解完上述五道例题后，我们可以发现「背包问题」的核心难点在于识别出这是一道「背包问题」。识别出是「背包问题」后，我们只需要观察每一个物品最多能取的次数，然后对应到具体的「0/1 背包」、「完全背包」、「多重背包」模型上即可推出对应的「DP 状态」以及「DP 转移方程」。为了方便大家后续查阅，现将上述三个背包模型总结如下：
BY /
本文作者：Gene_Liu编辑&版式：霍霍
https://baike.baidu.com/item/动态规划/529408?fr=aladdin
- 中文名
- 动态规划
- 外文名
- Dynamic Programming
- 所属学科
- 运筹学
- 简 称
- DP
- 运 用
- 求解决策过程（decision process）最优化的数学方法
- 第一本著作
- 《Dynamic Programming》
概念引入
基本思想
基本概念
-
多阶段决策问题
-
动态规划问题中的术语
基本结构
适用条件
-
最优化原理（最优子结构性质）
-
子问题的重叠性
