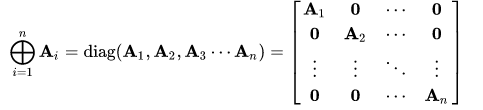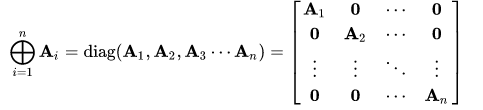小结：
1、xy平面 与 直和
https://en.wikipedia.org/wiki/Direct_sum
For example, the xy-plane, a two-dimensional vector space, can be thought of as the direct sum of two one-dimensional vector spaces, namely the x and y axes. In this direct sum, the x and y axes intersect only at the origin (the zero vector). Addition is defined coordinate-wise, that is 
, which is the same as vector addition.
Given two objects 
and 
, their direct sum is written as 
. Given an indexed family of objects 
, indexed with 
, the direct sum may be written 
. Each Ai is called a direct summand of A. If the index set is finite, the direct sum is the same as the direct product. In the case of groups, if the group operation is written as 
the phrase "direct sum" is used, while if the group operation is written 
the phrase "direct product" is used. When the index set is infinite, the direct sum is not the same as the direct product. In the direct sum, all but finitely many coordinates must be zero.
https://en.wikipedia.org/wiki/Matrix_addition
In general, the direct sum of n matrices is:
