[NOI2015]寿司晚宴
题目描述
为了庆祝NOI的成功开幕,主办方为大家准备了一场寿司晚宴。小G和小W作为参加NOI的选手,也被邀请参加了寿司晚宴。
在晚宴上,主办方为大家提供了n−1种不同的寿司,编号1,2,3,⋯,n-1,其中第种寿司的美味度为i+1(即寿司的美味度为从2到n)。
现在小G和小W希望每人选一些寿司种类来品尝,他们规定一种品尝方案为不和谐的当且仅当:小G品尝的寿司种类中存在一种美味度为x的寿司,小W品尝的寿司中存在一种美味度为y的寿司,而x与y不互质。
现在小G和小W希望统计一共有多少种和谐的品尝寿司的方案(对给定的正整数p取模)。注意一个人可以不吃任何寿司。
输入输出格式
输入格式:
从文件dinner.in中读入数据。
输入文件的第1行包含2个正整数n,p中间用单个空格隔开,表示共有n种寿司,最终和谐的方案数要对p取模。
输出格式:
输出到文件dinner.out中。
输出一行包含1个整数,表示所求的方案模p的结果。
输入输出样例
输入样例#1:
3 10000
输出样例#1:
9
输入样例#2:
4 10000
输出样例#2:
21
输入样例#3:
100 100000000
输出样例#3:
3107203
说明
【数据范围】
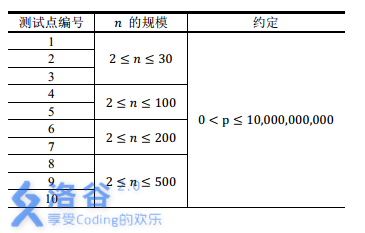
【时限1s,内存512M】
首先,选一个数就相当于把他的质因子全部选了,那么就先把每个数分解质因数.
因为sqrt(500)<23,所以只会有一个>=23的质因数和最多8个<23的质因数.
把<23的质因数状压,记为zt.还剩一个>23的质因数(没有就是1),记为zs.
安装zs排序,那么每个zs相同的都看做一块,这一块要么只能给A,要么只能给B,或者一个都没选.
设g[0/1][i][j]为两个人状态是i,j这一块给A/B的方案数.
主要枚举状态要从大往小枚举,避免重复统计.其实类似于01背包.
设f[i][j]为状态为i,j的方案数.
每次处理完一块用g来更新f.
f[i][j]=g[0][i][j]+g[1][i][j]-f[i][j].
重复统计了一个都没选的,把他减掉.
1 #include<bits/stdc++.h> 2 using namespace std; 3 long long f[260][260],g[2][260][260]; 4 int pm[8]={2,3,5,7,11,13,17,19}; 5 struct data{ 6 int zt,zs; 7 }q[510]; 8 long long ans=0; 9 const int c=(1<<8); 10 inline bool cmp(const data &A,const data &B){ 11 return A.zs<B.zs; 12 } 13 int main(){ 14 int n,mod; 15 scanf("%d%d",&n,&mod); 16 for(int i=2;i<=n;i++){ 17 int xx=i; 18 for(int j=0;j<8;j++){ 19 if(xx%pm[j]==0)q[i].zt|=(1<<j); 20 while(xx%pm[j]==0) xx/=pm[j]; 21 } 22 q[i].zs=xx; 23 } 24 f[0][0]=1; 25 sort(q+2,q+n+1,cmp); 26 for(int i=2;i<=n;i++){ 27 if(i==2 || q[i-1].zs!=q[i].zs || q[i].zs==1) memcpy(g[0],f,sizeof(f)),memcpy(g[1],f,sizeof(f)); 28 int now=q[i].zt; 29 for(int j=c-1;j>=0;j--) 30 for(int k=c-1;k>=0;k--) 31 if(!(j&k)){ 32 if(!(now&k)) g[0][j|now][k]+=g[0][j][k],g[0][j|now][k]%=mod; 33 if(!(now&j)) g[1][j][k|now]+=g[1][j][k],g[1][j][k|now]%=mod; 34 } 35 if(i==n || q[i].zs!=q[i+1].zs || q[i].zs==1) 36 for(int j=c-1;j>=0;j--) 37 for(int k=c-1;k>=0;k--) 38 if(!(j&k)) f[j][k]=(g[0][j][k]+g[1][j][k]-f[j][k]+mod)%mod; 39 } 40 for(int i=0;i<c;i++) 41 for(int j=0;j<c;j++) 42 if(!(i&j)) ans+=f[i][j],ans%=mod; 43 printf("%lld",ans%mod); 44 return 0; 45 }


