[NOI2011]Noi嘉年华

题目描述

NOI2011 在吉林大学开始啦！为了迎接来自全国各地最优秀的信息学选手，吉林大学决定举办两场盛大的 NOI 嘉年华活动，分在两个不同的地点举办。每个嘉年华可能包含很多个活动，而每个活动只能在一个嘉年华中举办。

现在嘉年华活动的组织者小安一共收到了 n个活动的举办申请，其中第 i 个活动的起始时间为 Si，活动的持续时间为Ti。这些活动都可以安排到任意一个嘉年华的会场，也可以不安排。

小安通过广泛的调查发现，如果某个时刻，两个嘉年华会场同时有活动在进行（不包括活动的开始瞬间和结束瞬间），那么有的选手就会纠结于到底去哪个会场，从而变得不开心。所以，为了避免这样不开心的事情发生，小安要求不能有两个活动在两个会场同时进行（同一会场内的活动可以任意进行）。

另外，可以想象，如果某一个嘉年华会场的活动太少，那么这个嘉年华的吸引力就会不足，容易导致场面冷清。所以小安希望通过合理的安排，使得活动相对较少的嘉年华的活动数量最大。

此外，有一些活动非常有意义，小安希望能举办，他希望知道，如果第i 个活动必须举办（可以安排在两场嘉年华中的任何一个），活动相对较少的嘉年华的活动数量的最大值。

输入输出格式

输入格式：

 

输入的第一行包含一个整数 n，表示申请的活动个数。

接下来 n 行描述所有活动，其中第 i 行包含两个整数 Si、Ti，表示第 i 个活动从时刻Si开始，持续 Ti的时间。

 

输出格式：

 

输出的第一行包含一个整数，表示在没有任何限制的情况下，活动较少的嘉年华的活动数的最大值。

接下来 n 行每行一个整数，其中第 i 行的整数表示在必须选择第 i 个活动的前提下，活动较少的嘉年华的活动数的最大值。

 

输入输出样例

输入样例#1：

5 
8 2 
1 5 
5 3 
3 2 
5 3 

输出样例#1：

2 
2 
1 
2 
2 
2 

说明

【样例说明】

在没有任何限制的情况下，最优安排可以在一个嘉年华安排活动1, 4，而在另一个嘉年华安排活动3, 5，活动2不安排。

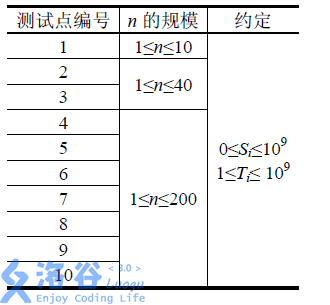
如果输出格式不正确（比如输出不足n+1行），得0分；

如果输出文件第一行不正确，而且后n行至少有一行不正确，得0分；

如果输出文件第一行正确，但后n行至少有一行不正确，得4分；

如果输出文件第一行不正确，但后n行均正确，得6分；

如果输出文件中的n+1行均正确，得10分。

 首先这道题每个点都给了4分的部分分.

那么先考虑40分的,就是没有限制的情况.

首先要将时间离散化.

先预处理一个东西,in[i][j]表示在时间[i,j]只内的活动的数量.这个怎么暴力怎么搞.

设f[i][j]表示时间到了i,一个选了j个活动,另一个的最大值.

那么转移就是f[i][j]=max(min(f[k][j]+in[k+1][i],f[i][j-in[k+1][i])).

就是枚举这一次选的哪些区间,是放到哪个嘉年华中.

然后40分就到手了..

考虑剩下的60分.

每次限制了一个区间必须选.

那么将状态转化一下,设num[i][j]表示必须选[i,j]内的区间,且没有其他选了的越过这个区间
的最大值.

设g[i][j]表示时间从后面到了i,一个选了j个活动,另一个的最大值.

这个和f就是反着的.

那么num[i][j]=max(min(x+y+in[i][j],f[i-1][x]+g[j+1][y])).

这样是n^4的,要考虑怎么优化.

可以看出来这个式子是具有单调性的.

当x增大时,y只有减小才能取得更大的答案.

所以就可以搞两个指针扫一遍即可,哪边大往哪边走.

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<map>
#include<complex>
#include<queue>
#include<stack>
#include<cmath>
#include<set>
#include<vector>
#define maxn 210
using namespace std;
struct data{
  int l,r;
}k[maxn];
int li[maxn*2],in[maxn*2][maxn*2],f[maxn*2][maxn],g[maxn*2][maxn],num[maxn*2][maxn*2],ans=0;
int main(){
  int n,tot=0;
  scanf("%d",&n);
  for(int i=1;i<=n;i++)
    scanf("%d%d",&k[i].l,&k[i].r),k[i].r=k[i].l+k[i].r-1,li[++tot]=k[i].l,li[++tot]=k[i].r;
  sort(li+1,li+tot+1);
  int p=unique(li+1,li+tot+1)-li-1;
  for(int i=1;i<=n;i++){
    k[i].l=lower_bound(li+1,li+p+1,k[i].l)-li;
    k[i].r=lower_bound(li+1,li+p+1,k[i].r)-li;
  }
  for(int i=1;i<=p;i++)
    for(int j=i;j<=p;j++)
      for(int l=1;l<=n;l++)
    if(k[l].l>=i && k[l].r<=j) in[i][j]++;
  memset(f,-127/3,sizeof(f));memset(g,-127/3,sizeof(g));
  for(int i=0;i<=p+1;i++)
    f[i][0]=0,g[i][0]=0;
  f[1][0]=in[1][1],f[1][in[1][1]]=0;
  g[p][0]=in[p][p],g[p][in[p][p]]=0;
  for(int i=0;i<=p+1;i++)
    for(int j=0;j<=n;j++)
      for(int k=0;k<i;k++){
    int l=max(f[k][j]+in[k+1][i],(j-in[k+1][i]>=0)?f[k][j-in[k+1][i]]:0);
    f[i][j]=max(f[i][j],l);
    ans=max(ans,min(j,f[i][j]));
      }
  printf("%d\n",ans);
  for(int i=p+1;i>=0;i--)
    for(int j=0;j<=n;j++)
      for(int k=p+1;k>i;k--){
    int l=max(g[k][j]+in[i][k-1],(j-in[i][k-1]>=0)?g[k][j-in[i][k-1]]:0);
    g[i][j]=max(g[i][j],l);
      }
  memset(num,-127/3,sizeof(num));
  for(int i=0;i<=p+1;i++)
    for(int j=i;j<=p+1;j++){
      int l=0,r=n;
      while(l<=n && r>=0){
    int x=min(l+1+r+in[i][j],f[i-1][l+1]+g[j+1][r]);
    int y=min(l+r-1+in[i][j],f[i-1][l]+g[j+1][r-1]);
    //if(max(x,y)<num[i][j]) break;
    if(x<y) r--,num[i][j]=max(num[i][j],y);
    else l++,num[i][j]=max(num[i][j],x);
      }
      //num[i][j]=ans;
    }
  for(int i=1;i<=n;i++){
    ans=0;
    for(int j=0;j<=k[i].l;j++)
      for(int w=k[i].r;w<=p+1;w++)
    ans=max(ans,num[j][w]);
    printf("%d\n",ans);
  }
  return 0;
}