对抗遗忘的算法

一年多前，为了学习英语，我设计了一个学习英语的 web 程序，采用了固定的学习间隔：

1天，2天，4天，7天，15天，30天，90天，180天，1年，两年..(从网上找来的一种通用的艾宾浩斯间隔)
后记：艾宾浩斯发表的仅仅只有他的曲线，这种间隔方案不知道是谁发明的，没有相关资料

这种学习方式太死板，主要问题是：

1. 对于简单的单词没必要这么频繁，每天学习新单词的堆积，会造成有一天需要同时复习大量的单词
2. 难的单词又需要更加紧凑的复习间隔，否则往往在第7天、30天、90天，又得重新推翻其复习间隔，再次从 1 天开始

也就是说，我需要一种根据我的记忆情况，调整新的复习间隔
于是最近几天，我开始考虑新的记忆方案，找了许久终于找到了一种符合我的要求的，关于遗忘的算法: SM-2

SM-2 算法，是 SuperMemo(一种主流的记忆软件)的第二代的算法，开源。是现今主流的算法，被 Anki（也是主流的记忆软件）采用
值得一提的是，SuperMemo 已经更新到 18 代了，18 代有啥优势，暂且不表

SM-2 算法代码实现

SM-2 算法伪代码：

1. Split the knowledge into smallest possible items.
2. With all items associate an E-Factor equal to 2.5.
3. Repeat items using the following intervals:
   I(1):=1
   I(2):=6
   for n>2: I(n):=I(n-1)*EF
   where:
   I(n) – inter-repetition interval after the n-th repetition (in days),
   EF – E-Factor of a given item
   If interval is a fraction, round it up to the nearest integer.
4. After each repetition assess the quality of repetition response in 0-5 grade scale:
   5 – perfect response
   4 – correct response after a hesitation
   3 – correct response recalled with serious difficulty
   2 – incorrect response; where the correct one seemed easy to recall
   1 – incorrect response; the correct one remembered
   0 – complete blackout.
5. After each repetition modify the E-Factor of the recently repeated item according to the formula:
   EF’:=EF+(0.1-(5-q)(0.08+(5-q)0.02))
   where:
   EF’ – new value of the E-Factor,
   EF – old value of the E-Factor,
   q – quality of the response in the 0-5 grade scale.
   If EF is less than 1.3 then let EF be 1.3.
6. If the quality response was lower than 3 then start repetitions for the item from the beginning without changing the E-Factor (i.e. use intervals I(1), I(2) etc. as if the item was memorized anew).
7. After each repetition session of a given day repeat again all items that scored below four in the quality assessment. Continue the repetitions until all of these items score at least four.

TypeScript 实现：

export type SuperMemo2Item = {
    interval: number, // 下一次的复习周期，默认 0，表示当天第一次复习
    EF: number, // easer factor，容易度因子
}
export type SuperMemo2ReturnItem = {
    interval: number,
    EF: number,
    isRepeat: boolean,
}

export type SuperMemo2Quality = 5 | 4 | 3 | 2 | 1 | 0;

const getEF = (EF: number, quality: SuperMemo2Quality) => {
    const ans = EF + (0.1 - (5 - quality) * (0.08 + (5 - quality) * 0.02));
    if (ans < 1.3) {
        return 1.3;
    }
    // 在算法 SM-0 中, EF 范围是 [1.3,2.5]，不知道 SM2 是啥
    // if (ans > 2.5) {
    //     return 2.5
    // }
    return ans;
}


const SuperMemo2 = (item: SuperMemo2Item, quality: SuperMemo2Quality): SuperMemo2ReturnItem => {
    // 下一次的因子
    const _EF = getEF(item.EF, quality);
    // 下一次的间隔
    let _interval: number;

    if (quality < 3) {
        _interval = 1;
    } else if (quality === 3) {
        _interval = item.interval === 0 ? 1 : item.interval;;
    } else {
        if (item.interval === 0) {
            _interval = 1;
        } else if (item.interval === 1) {
            _interval = 6;
        } else {
            _interval = Math.ceil(item.interval * item.EF);
        }
    }
    return {
        EF: _EF,
        interval: _interval,
        isRepeat: quality < 4,
    }
}


export default SuperMemo2;

使用

我是学习单词的，每一天的单词，每个单词只调用一次这个函数，不可以反复调用，然后根据是否重复复习标志，进行复习。
下面是我单词在数据库中存放的结构：

字段	类型	释义
id	int(11)
f	double	EF，默认 2.5
i	int(11)	interval 间隔，默认 0
r	int(11)	repetition 重复次数，默认 0
d	int(11)	date 复习日期，采用 unix 时间(秒)

设定今日学习终止时间，这里设定为 dueDate，我自己设置的是晚上 24点前，所以 dueDate 是 23:59:59 的 unix 时间戳（秒）：

1. 调取数据库小于dueDate 的单词，开始学习单词，根据打分情况调用 SuperMemo2 函数
2. 如果 isRepeat === false，根据 i 更新 d（此时 d 至少是 1 天后了 ），结束学习
3. 如果 isRepeat === true，开启复习模式
4. 复习模式（注意 d 不能超过dueDate，我这里是不能超过今晚 24点）：

打分 0，更新 r+=4（注意这里我限制了 r 最大为4，不然复习太多次），更新 d 为5分钟后
打分 1，更新 r+=3，更新 d 为30分钟后
打分 2，更新 r+=2，更新 d 为120分钟后
打分 3，更新 r+=1，更新 d 为180分钟后
打分 4、5，更新 r-=1，更新 d 为180分钟后

5. 直到 r<=0，进入步骤2，结束学习

关于间隔，我插一嘴，我曾经以为是，今天1号，间隔 1天，那么下一次的复习日期就是3号。其实不是的，应该是2号
还有就是 anki 软件的周期，不同于 supermemo2（第一次间隔 1，第二次间隔 6，第三次....）, anki 第二次的间隔是 4

评价

EF因子越大，则复习周期越长。否则，复习周期越短，复习就越频繁，EF 最低是 1.3：

EF 为 1.3 的时候，一年内的复习间隔序列是 [1, 6, 8, 11, 15, 20, 26, 34, 45, 59, 77, 101]
当然，要是学习成果不佳，就会从头开始复习周期

从长期的复习曲线来看，越容易的复习间隔越长，越简单的复习间隔越短复习越频繁！，下面是 SuperMemo2 算法和艾宾浩斯曲线的对比图：

其他

官网 SM-2 算法讲解
SuperMemo - 百度百科
其他人的 SM-2 算法 javascript 代码实现

后续

现在是两个月后，我写下了后续。最近准备考研，在复习高等数学。
学到指数函数，灵光一闪，发现遗忘曲线就是个指数函数，而且这个遗忘算法也是指数函数:

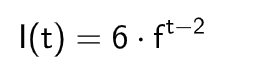
其中，t是第几次复习，t大于等于2，f是相关因子
这个函数的实际意义就是第二轮复习起，每轮的间隔

设x=t-2，则有：

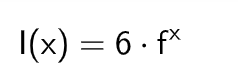
调整成指数增长方程：

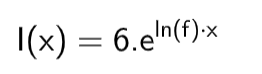
发现f是增长常数，初始总数是6

在上面的指数增长方程可以发现，增长常数只依赖单一因子 EF
但是在supermemo17的算法中，采取了双因子模型，两个因子影响增长常数
在知乎关于supermemo板块经常看见的叶峻峣同学，他的论文已经涉及到三个因子，他公开了算法，参阅