线性规划入门
引入
线性规划是运筹学的一个重要分支，在实际生活中应用非常广泛，其核心问题是如何在资源有限（人力、物力、时间等）的前提下作出最优决策。
以最经典的生产模型为例：
某工厂能生产甲、乙、丙三种产品，生产每种产品都同时需要原料 A 和原料 B 并花费一定工时。同时，由于原料供应链及生产设备限制，每日能使用的原料以及机器工时有限，具体如下表所示。问，应如何安排生产才能使得每日利润最大？
| 甲 | 乙 | 丙 | 每日上限 | |
|---|---|---|---|---|
| 原料 A | 2 | 3 | 2 | 200 |
| 原料 B | 4 | 3 | 1 | 300 |
| 工时 | 2 | 5 | 7 | 500 |
| 利润 | 2 | 3 | 3 | - |
设甲、乙、丙的每日生产数量为 \(x_1, x_2, x_3\)，目标是利润最大化，即
由原料及工时的限制，得
\(x_1, x_2, x_3\) 具有实际意义，因此
其中 (a1) 式称为目标函数，(a2) ~ (a5) 式称为约束条件，记为 s.t. (即 subject to)
诸如此例中的问题便是线性规划问题——在满足约束条件的前提下，使目标函数最大化（或最小化）。
线性规划-标准形式
线性规划的形式多样，目标函数可以为最大化或最小化，约束条件可以为等式或不等式，变量则可以为任意实数。但无论哪种形式的线性规划，都可以化为统一的标准形式。
标准形式如下：
在标准形式中，目标函数为最大化，所有约束条件均为小于等于，所有变量均为非负实数
按以下方法可以将其它形式的线性规划转化为标准形式：
- 若目标为最小化，则将目标函数取反改为最大化
- 若某约束条件为等式，则将其拆分为大于等于和小于等于两条不等式
- 若某约束条件为大于等于，则将不等式两边同时取反，改为小于等于
- 若某变量 \(x\) 没有非负约束，则定义两个新的非负变量 \(x',x''\)，用 \(x'-x''\) 替换原有的变量 \(x\)
注意：
-
之所以没有考虑约束条件为大于或小于的情况，是因为线性规划的最优解总在边界上取得，如果不允许取边界值，那么最优解存在但取不到，通常也不会有不能取边界值的情况。
-
诸如 \(x', x''\) 等引入的新变量并没有实际意义，仅仅是数学上的技巧。或者说，一旦将原问题抽象为线性规划后我们便仅从数学的角度考虑问题。
线性规划-松驰形式
在将线性规划统一为标准形式之后，为了方便计算，我们还需进一步将标准形式转化为松驰形式。
松驰形式如下：
松驰形式与标准形式类似，区别在于松驰形式的约束条件为等式。因此，将标准形式转为松驰形式的方法也很简单，对于标准形式中的第 \(j\) 条约束条件
引入一个松驰变量 \(x_{n+j}\) ，将不等式转为等式
移项，便得到了松驰形式的约束条件
我们将等式左边的变量 \(x_{n+1}, x_{n+2}, ..., x_{n+m}\) 称为基变量，剩下的变量 \(x_1, x_2, ..., x_n\) 称为非基变量。
基变量不会出现在目标函数中，同时除了非负约束，基变量仅包含在一个约束条件中，也就是说基变量的约束是相对最宽松的。
线性规划的解
补充几个线性规划解的概念：
基本解：非基变量全部为零的解
可行解：满足所有约束条件的解
基本可行解：可行解中的基本解
最优解：可行解中能使得目标函数最大化（最小化）的解
Venn 图表示如下：
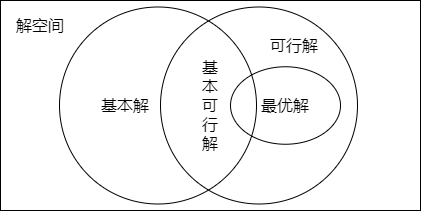
可以证明的是，基本可行解中一定存在最优解
求解线性规划-单纯形法
单纯形法是最经典的求解线性规划的方法，其核心操作是转轴（pivot）操作，即选择一个基变量和一个非基变量，分别称为出基变量和入基变量，令出基变量出基变为非基变量，入基变量则入基变为基变量。这里用开篇引入的例子介绍单纯形法：
该线性规划已经是标准型，将其进一步转化为松驰型：
对于一个松驰形式的线性规划，如果约束条件中的常数 b 均非负，我们可以令所有非基变量为零，得到一个基本可行解。在本例中，令 \(x_1, x_2, x_3\) 等于零，得到基本可行解 \((0, 0, 0, 200, 300, 500)\) ，此时目标函数值为 0。观察目标函数，发现函数中变量的系数均大于零，增大 \(x_1, x_2, x_3\) 中任意一个变量都能使目标函数增大。
接下来进行转轴操作，先选择入基和出基变量。由于 \(x_2\) 的系数最大，对增大目标函数的贡献最大，因此选择 \(x_2\) 作为入基变量（系数相同时选下标小的）。出基变量的选择需要考虑约束条件，由于变量的非负约束，\(x_2\) 不能无限增大，由 (b1) 及 \(x_4 \geq 0\) 得 \(x_2 \leq 200/3\)，由 (b2) 及 \(x_5 \geq 0\) 得 \(x_2 \leq 100\)，由 (b3) 及 \(x_6 \geq 0\) 得 \(x_2 \leq 100\)。为同时满足这 3 个条件，我们需满足最紧的约束 \(x_2 \leq 200/3\)， 因此 (b1) 所对应的基变量 \(x_4\) 作为出基变量。
选定变量后，我们将 \(x_2\) 入基，\(x_4\) 出基，操作上便是将 \(x_2\) 移项到式子左边，\(x_4\) 移项到式子右边，(b1) 式子化为
将其代入目标函数及其它约束条件得
转轴后，同样令非基变量等于零，得到基本可行解 \((0, \frac{200}{3}, 0, 0, 100, \frac{500}{3})\) ，此时目标函数的值增大至 200。经过转轴后的线性规划仍为松驰形式，且没有破坏常数 b 非负性（通过计算不难证明）。
此时目标函数中仍有正系数，因此还能增大，继续转轴。同样地，先通过目标函数系数选择入基变量，再通过基变量对入基变量的约束选择出基变量。如果所有基变量均对入基变量没有约束，则说明该线性规划的解无界 。 本例中此时入基变量只能选 \(x_3\)，约束条件中 \(x_5\) 对 \(x_3\) 没有约束，但 \(x_2, x_6\) 有，且 \(x_6\) 对 \(x_3\) 的约束最紧，作为出基变量。同样移项并代入，得
令非基变量等于零，得到基本可行解 \((0, \frac{400}{11}, \frac{500}{11}, 0, \frac{160}{11}, 0)\) ，目标函数的值继续增大至 \(2700/11\)。以此类推，通过计算不难得出每次转轴操作中目标函数的增量为 \(c_ib_j/A_{j, i}\) ，\(b_j\) 在转轴过程中保持非负，我们通过对入基和出基变量的选择保证了 \(c_i, A_{j, i}\) 也非负，因此 \(c_ib_j/A_{j, i} \geq 0\)，目标函数在每次转轴后只增不减。
以此类推，不断转轴直至目标函数中所有变量的系数均不大于零，此时无论增大哪个变量都只会使目标函数减小，一个局部最优解便找到了。可以证明线性规划问题的局部最优解同时也是全局最优解，于是线性规划的最优解也就得到了。
简单来说，单纯形法就是通过变量的等量代换不断迭代从而逐步逼近并取得最优解。
初始化
单纯形法的转轴操作是以常数 \(b\) 均非负为前提的，对于常数 \(b\) 不全非负的线性规划，我们可以先找到一个基本可行解，而后作为初始值用单纯形法求最优解。
为找到一个基本可行解，可以引入一个辅助线性规划：
对于原线性规划中的任意一个可行解 \((a_1, a_2, ..., a_{n+m})\) ，\((0, a_1, a_2, ..., a_{n+m})\) 是其对应辅助线性规划的可行解，且由于 \(x_0 \geq 0\) ，该解同时也是辅助线性规划的最优解。
反过来，如果辅助线性规划的最优解为 0，即 \(-x_0 = 0\) ，那么将 \(x_0\) 从约束条件中删去，约束条件等式两边仍然相等，此时约束条件与原线性规划等价，因此我们可以用其等价替代原线性规划的约束条件。由于用单纯形法求解辅助线性规划的过程会保证常数 b 的非负性，因此替代后常数 b 均非负，这时便可以用单纯形法求解原线性规划了。
那么问题便转化为如何找到辅助线性规划的初始解，这不难构造。首先选定 \(x_0\) 为入基变量，找到 \(b\) 中的最小值 \(b_k\)（小于零），将对应的 \(x_{n+k}\) 作为出基变量，移项得
而后将其代入目标函数及其它约束条件中，便完成了转轴操作。由于选取的 \(b_k\) 为 \(b\) 中的最小值，因此代入后的各约束条件中的常数 \(b_i\) 均非负。接下来就可以用单纯形法求解辅助线性规划了。
理论上无论什么线性规划都可以通过上述初始化方法找到初始基本可行解，但初始化的过程也需要用单纯形法，即同一问题跑了两遍单纯形法，有时初始化的过程还可能破坏题目原有的一些性质，导致计算时间大幅增加。此外，初始化的代码较为繁琐，写起来也容易出错。综合来看，我们并不能对线性规划盲目初始化，一般会尽量通过其它方法找到初始基本可行解以规避初始化过程。
算法复杂度
在转轴操作中采用 Bland's 法则，即值相同时选下标最小的，可以证明此时单纯形法一定能在有限步内终止。单纯形法最坏情况下的时间复杂度为指数级别，且有构造出让单纯形法的复杂度达到指数级的方法，不过需要出题人刻意留心卡单纯形法。多数情况下（如随机数据）单纯形法的效率还算令人满意。
对偶线性规划
每个线性规划都可以找到与其等价的对偶线性规划，还是借用开篇中的例子，修改一下问题，假设某老板想要租用工厂一天，问最少应支付多少租金。
| 甲 | 乙 | 丙 | 每日上限 | |
|---|---|---|---|---|
| 原料 A | 2 | 3 | 2 | 200 |
| 原料 B | 4 | 3 | 1 | 300 |
| 工时 | 2 | 5 | 7 | 500 |
| 利润 | 2 | 3 | 3 | - |
租用工厂可以看成收购工厂一天内的所有资源，包括原料和工时，设原料 A、原料 B 以及工时的单位收购价格为 \(y_1,y_2,y_3\) ，老板的目标是总租金最小化。即：
对于厂主来说，如果租金小于原有的利润，就不会答应租借，因此约束条件为：
这个线性规划与开篇中的线性规划其实是等价的，尽管目标函数和约束条件不同，但最优解是相同的，区别是两者站在了不同的角度描述问题，我们称这两者互为对偶线性规划。
如果我们用矩阵来描述线性规划的标准形式：
那么对于任意线性规划，其对偶线性规划为：
前面提到，求解线性规划时要尽量避免初始化，一个常用的方法便是利用对偶线性规划，部分原本需要初始化的线性规划在转化为对偶线性规划后可以直接找到初始基本解。
单纯形法的算法实现
通过上文的讲解，我们已经知道了单纯形法的算法流程，代码实现上其实并没有太多思维上的难度，主要是流程比较繁琐，写的时候很容易出错，把它当成大模拟题来写就行了。
值得注意的是，如果一个线性规划有 \(n\) 个变量 \(m\) 个约束条件，那么通常需要 \(m\) 行 \(n+m\) 列（因为引入了 \(m\) 个松驰变量）的二维数组，而其对偶线性规划则需要 \(n\) 行 \(n+m\) 列的二维数组。所以如果 \(m > n\) ，通过转化为对偶线性规划可以达到节省数组空间提高计算速度的目的。但实际上我们可以单独保存这 \(m\) 个松驰变量，类似稀疏链表的存储方式，这样可以节省大量的数组空间。
模板
这里提供一份个人使用的代码模版供大家参考使用，有些地方写得比较繁琐，将就一下。这份代码通过了 200 万组随机数据的测试，应该是没有什么大问题的的。
#include<bits/stdc++.h>
const double eps = 1e-8;
#define eq(a, b) (fabs((a)-(b)) < (eps))
#define ge(a, b) (((a)-(b)) > (eps))
using namespace std;
struct LP //Linear Programming，标准型：max <=
{
int r, c, tc; //r行c列矩阵，tc实际总列数(即包括单位矩阵)
double M[1005][2005], tmp[3005];
//第0行存放目标函数，第0列存放常数b，中间存放约束条件系数矩阵
//所有位置都是从1开始存放，最终结果存放在M[0][0]处
int Bx[3005]; //存放基变量，key为变量编号、val为所在行
int Fy[3005]; //存放非基变量，key为变量编号、val为所在列
//数组大小关系：M[r][c], tmp[tc], Bx[tc], Fy[tc]
void pivot(int id, int x, int y) //转轴，参数为入基变量编号及所在行、列
{
for (int i = 1; i < tc; i++) //根据入基变量所在行查找出基变量，出基
if (Bx[i] == x)
{
Bx[i] = 0;
Fy[i] = y;
break;
}
Fy[id] = 0; //入基变量入基
Bx[id] = x;
}
void gos(int x, int y) //高斯消元，用于消去其它式子中的入基变量，参数为入基变量所在行、列
{
double tmp = M[x][y];
for (int i = 0; i <= c; i++) M[x][i] /= tmp;
M[x][y] = 1/tmp;
for (int i = 0; i < r; i++) //入基变量所在列需特殊处理，转化为出基变量所在列
if (i != x && !eq(M[i][y], 0))
{
tmp = M[i][y];
for (int j = 0; j <= c; j++) M[i][j] -= tmp*M[x][j];
M[i][y] = -tmp*M[x][y];
}
}
bool simplex() //单纯形法
{
while (1)
{
int id, x, y = 0;
for (int i = 1; i < tc; i++) //查找目标函数的最大系数，对应入基变量所在列
if (Fy[i] && (y == 0 || ge(M[0][Fy[i]], M[0][y]))) id = i, y = Fy[i];
if (!ge(M[0][y], 0)) return 0; //最大系数小于0，说明已达到最优解
for (x = 1; x < r && !ge(M[x][y], 0); x++) ; //找到该列中第一个系数a>0的位置
if (x == r) return 1; //该列系数均不大于0时，说明为无界解
for (int i = x+1; i < r; i++) //在该列所有a>0处中找b/a最小处，对应入基变量所在行
if (ge(M[i][y], 0) && ge(M[x][0]/M[x][y], M[i][0]/M[i][y])) x = i;
pivot(id, x, y); //确定入基变量的x、y后，转轴
gos(x, y); //消去其它式子中的入基变量
}
}
bool init() //初始化，寻找初始基本可行解，b全非负时不能初始化
{
for (int i = 1; i < tc; i++) tmp[i] = Fy[i] ? M[0][Fy[i]] : 0;
for (int i = 0; i < c; i++) M[0][i] = 0; //另存并清空目标函数
for (int i = 1; i < r; i++) M[i][c] = -1;
M[0][c++] = -1; //加入辅助变量x'，列数加1
int id = tc++, x = 1, y = c-1; //新变量id为tc，所在列为c-1，作为入基变量
Fy[id] = y;
for (int i = 1; i < r; i++) //查找b中最小值，对应入基变量所在行
if (ge(M[x][0], M[i][0])) x = i;
pivot(id, x, y); //入基变量所在列为c-1
gos(x, y);
simplex(); //求解辅助线性规划
if (ge(M[0][0], 0)) return 1; //当辅助线性规优最优解不为零时原线性规划无解
//基变量中含有x'时需要出基，这不会使目标函数的值变化
if (Bx[tc-1])
{
x = Bx[tc-1];
for (id = 1; !Fy[id] || eq(M[x][Fy[id]], 0); id++) ; //任选一个x行不为0的非基变量入基
y = Fy[id];
Bx[id] = x; Fy[id] = 0;
Fy[tc-1] = y; Bx[tc-1] = 0;
gos(x, y);
}
for (id = 1; Fy[id] != c-1; id++);
for (int i = 0; i < r; i++) swap(M[i][Fy[tc-1]], M[i][Fy[id]]);
Fy[id] = Fy[tc-1];
Bx[tc-1] = 0;
Fy[tc-1] = 0;
c--, tc--; //删云辅助变量x'
for (int i = 1; i < tc; i++)
if (Fy[i]) M[0][Fy[i]] = tmp[i]; //还原目标函数
for (int i = 1; i < tc; i++) //消去目标函数中的基变量
{
if (Bx[i] && !eq(tmp[i], 0))
{
for (int j = 0; j < c; j++) M[0][j] -= tmp[i]*M[Bx[i]][j];
}
}
return 0;
}
void getans() //求各变量最终取值，保存在tmp中
{
for (int i = 1; i < c; i++)
tmp[i] = Bx[i] ? M[Bx[i]][0] : 0;
}
void solve (int n, int m) //n个变量，m个约束
{
r = m+1, c = n+1, tc = n+m+1;
memset(Fy, 0, sizeof(Fy));
memset(Bx, 0, sizeof(Bx));
for (int i = 1; i <= n; i++)
Fy[i] = i;
for (int i = 1; i <= m; i++) //引入松驰变量
Bx[n+i] = i;
if (init()) {printf("No Solution\n"); return;} //部分题中不需要初始化，强行初始化出错
if (simplex()) {printf("Unbounded\n"); return;}
//在此输出结果...
//getans();
printf("%.0f\n", -M[0][0]); //结果要取反
}
}lp;
int main()
{
int n, m;
while (scanf("%d%d", &n, &m) != EOF)
{
//根据题意求出方程在此处填写矩阵...
lp.solve(n, m);
}
return 0;
}
例题
Happiness
Nasa 需要为 \(m\) 名 ACM 参赛选手准备食物，他决定为所有选手准备相同的套餐，套餐由 \(n\) 种不同的食物组成，价格为分别为 \(c_i\)。由于口味不同，不同人吃一个单位的某种食物所获得的满足感可能不同，\(i\) 号选手吃 \(j\) 号食物所得满足感为 \(a_{ij}\)，同时每个人的满足感上限为 \(b_i\)。为了不浪费食物，求在不超过任何人的满足感的前提下 Nasa 最多能花费多少钱。
设第 \(i\) 种食物准备 \(x_i\) 个单位，目标函数为最大化花费：
约束条件为不超过任何人的满足感上限：
建模出来刚好为线性规划标准形，直接跑单纯形法即可。
战线防守
现在需要在一条长度为 \(n\) 的序列上建塔来防守敌兵，在序列第 \(i\) 号位置上建一座塔的花费为 \(c_i\)，且一个位置可以建任意多的塔，费用累加计算。有 \(m\) 个区间 \([L_1, R_1], [L_2, R_2], ..., [L_m, R_m]\)，在第 \(i\) 个区间的范围内要建至少 \(D_i\) 座塔，求最少花费。
设在 \(i\) 位置上建立 \(x_i\) 座塔，目标函数为最小化总花费：
约束条件为各区间内塔的数目足够多：
将其转化为对偶线性规划，可以直接找到初始基本可行解 \((0,0,...,0)\) 从而避开初始化。
Cashier Employment
一家 24 小时超市需要雇佣一些员工，将一天均分为 24 个时间段，超市每天的不同时间段需要不同数量的员工 \(b_i\)，同一时间段内每天需要的员工数是相同的。现有 \(n\) 个人可以雇佣，固定每天从 \(t_i\) 点钟开始，连续工作 8 个小时。求在满足人员数量要求的前提下，最少需要雇佣的员工数。
首先将 \(n\) 个人按工作时间分为 24 类，每类分别有 \(k_i\) 人，设每类雇佣 \(x_i\) 人，目标函数为最小化总员工数：
约束条件为每类员工的人数限制以及每个时间段的员工数限制：
转为标准形后无法直接找到初始可行解，同样可以转为对偶线性规划解决。
Freelancer's Dreams
某人梦想成为一流程序员并购买一套房，这需要 \(p\) 点经验 \(q\) 点金钱。有 \(n\) 份兼职，一天分别能获得 \(a_i\) 经验和 \(b_i\) 金钱，他可以随时更换兼职，但不能同时干多份兼职，问他最少需多少天才能实现梦想，结果可以为小数。
设第 \(i\) 份工作干 \(x_i\) 天，目标函数为最小化工作天数
约束条件显然为经验和金钱：
转为标准形后常数为负，无法直接找到初始可行解，如果转为对偶线性规划，在引入松驰变量后矩阵会变得非常大，因此最终选择直接辅助线性规划进行初始化。当然，其实该线性规划可以用半平面交解，不过就是另一个话题了。
