[洛谷] P4348 Cow Confinement（扫描线）

传送门： Cow Confinement

思路：
先考虑一个更简单的问题，如果没有围栏的限制，只有花和牛。对于这个简化的问题，由于牛只可以向 x 或 y 增大的方向移动，所以我们可以用一条平行于 x 轴的扫描线，按 y 轴从大到小扫描：

如果遇到花，就在数状数组对应位置权值加 1
如果遇到牛，查询 [x, inf] 区间上包括的花的数量（x 为牛所处位置），查询结果即为该头牛能到达的花的数量

再来考虑围栏，这时由于遮挡，每头牛能访问的区间为 [x, nex]，nex 为每头牛右侧第一个竖直围栏的位置，题目给定了网格的范围为 \(10^6 \times 10^6\)，所以我们可以假定整个网格被一个巨大的围栏围起来，这样一来每头牛的右侧一定能找到一个围栏，每次在所有竖直围栏里二分查找每头牛右侧的围栏。即然是扫描线，竖直围栏所处的位置一定是动态地增减的，所以自然地能想到用 set 来维护竖直围栏的位置。

我们将一个矩形围栏周围的八个方位划分为八个区域，如图

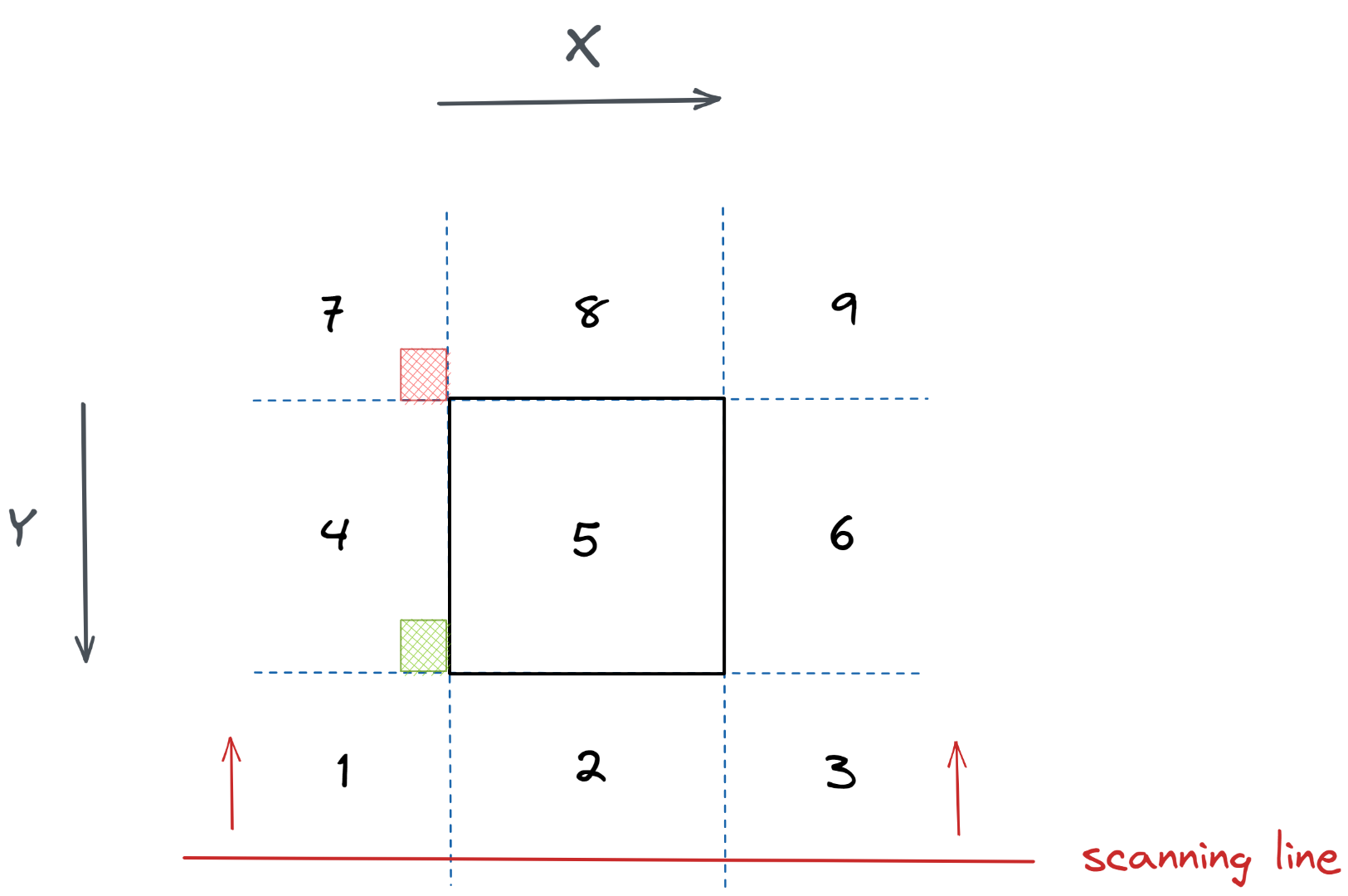
根据刚才所说，4 区域的牛能访问 1、4 区域，但单纯计入这部分花是有所遗漏的，4 区域的牛显然还能访问 2、3 区域，这部分的花也需要被计入。所以我们可以在扫描线扫到围栏的底边时将 2、3 区域的花全部累加到 4 区域的右下角（绿色正方形处），这样就能被一同计入。

5 区域由于被围栏围起来，即不能访问其它区域、也无法被其它区域访问，所以在扫描到围栏底边和顶边时，将分别 2、5 区域的权值清空。

7 区域的牛能访问到 5 以外所有区域，其中 2 区域的权值虽然被清空了，但由于被复制到了 4 中，仍能被累加到，但 3 区域的权值却会被累计了两次，所以需要在遇到顶边时相应地在（红色）位置扣除这部分权值。

代码实现上，由于数据范围在 \(10^6\) 以内且为整数，因此不需要离散化，围栏的位置使用 multiset 来存，因为可能会出现位于同一位置的围栏。对于同一 y 处的边应先处理底边再处理顶边，因为处理底边时需要求查询区间，相同 y 值的顶边此时仍能起到遮挡作用

这题实在是太麻烦了，写了整整一天，十分感谢 starusc 大佬，看了他的题解才搞明白的。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef tuple<int, int, int> tup;
#define fsio ios::sync_with_stdio(false)
#define ls (t<<1)
#define rs (t<<1|1)
const int inf = 0x3f3f3f3f;
const int maxn = 1e6+10;

int vsum[maxn<<2], vset[maxn<<2], ans[maxn<<2], save[maxn];

struct node
{
    int tp, y, a, b, c;
    bool operator < (const node &b) const
    {
        if (y == b.y) return tp < b.tp;
        return y > b.y;
    }
}eg[maxn];

void pushup(int t)
{
    vsum[t] = vsum[ls] + vsum[rs];
}

void pushdown(int t)
{
    if (!vset[t]) return;
    vset[ls] = vset[rs] = 1;
    vsum[ls] = vsum[rs] = 0;
    vset[t] = 0;
}

void build(int t, int tl, int tr)
{
    vsum[t] = vset[t] = 0;
    if (tl == tr) return;
    int mid = (tl+tr)>>1;
    build(ls, tl, mid);
    build(rs, mid+1, tr);
}

void clear(int t, int tl, int tr, int l, int r)
{
    if (tl > r || tr < l) return;
    if (l <= tl && tr <= r)
    {
        vsum[t] = 0;
        vset[t] = 1;
        return;
    }
    int mid = (tl+tr)>>1;
    pushdown(t);
    clear(ls, tl, mid, l, r);
    clear(rs, mid+1, tr, l, r);
    pushup(t);
}

void update(int t, int tl, int tr, int pos, int k)
{
    if (tl > pos || tr < pos) return;
    if (tl == tr)
    {
        vsum[t] += k;
        return;
    }
    int mid = (tl+tr)>>1;
    pushdown(t);
    update(ls, tl, mid, pos, k);
    update(rs, mid+1, tr, pos, k);
    pushup(t);
}

ll query(int t, int tl, int tr, int l, int r)
{
    if (tl > r || tr < l) return 0;
    if (l <= tl && tr <= r) return vsum[t];
    int mid = (tl+tr)>>1;
    pushdown(t);
    return query(ls, tl, mid, l, r) + query(rs, mid+1, tr, l, r);
}

int main()
{
    int f, n, m;
    while(cin>>f)
    {
        int tot = 0, mx = 1e6+1;
        for (int i = 0; i < f; i++)
        {
            int x1, y1, x2, y2;
            cin>>x1>>y1>>x2>>y2;
            eg[tot++] = {0, y2, x1, x2, i};
            eg[tot++] = {1, y1-1, x1, x2, i};
        }
        cin>>m;
        for (int i = 0; i < m; i++)
        {
            int x, y;
            cin>>x>>y;
            eg[tot++] = {2, y, x, 0, 0};
        }
        cin>>n;
        for (int i = 0; i < n; i++)
        {
            int x, y;
            cin>>x>>y;
            eg[tot++] = {3, y, x, i, 0};
        }
        sort(eg, eg+tot);
        build(1, 0, mx);
        multiset<int> st;
        st.insert(mx);
        for (int i = 0; i < tot; i++)
        {
            if (eg[i].tp == 1)
            {
                auto [a, b, x1, x2, id] = eg[i];
                update(1, 0, mx, x1-1, -save[id]);
                clear(1, 0, mx, x1, x2);
                st.erase(x1-1);
                st.erase(x2);
            }
            else if (eg[i].tp == 0)
            {
                auto [a, b, x1, x2, id] = eg[i];
                int nex = *st.upper_bound(x2);
                save[id] = query(1, 0, mx, x2+1, nex);
                update(1, 0, mx, x1-1, query(1, 0, mx, x1, nex));
                clear(1, 0, mx, x1, x2);
                st.insert(x1-1);
                st.insert(x2);
            }
            else if (eg[i].tp == 2)
            {
                auto [a, b, x, c, d] = eg[i];
                update(1, 0, mx, x, 1);
            }
            else
            {
                auto [a, b, x, id, c] = eg[i];
                int nex = *st.lower_bound(x);
                ans[id] = query(1, 0, mx, x, nex);
            }
        }
        for (int i = 0; i < n; i++)
        {
            cout<<ans[i]<<endl;
        }
    }
    return 0;
}