高数(01)--函数、极限、连续

高数(1)--函数、极限、连续

极限

极限定义

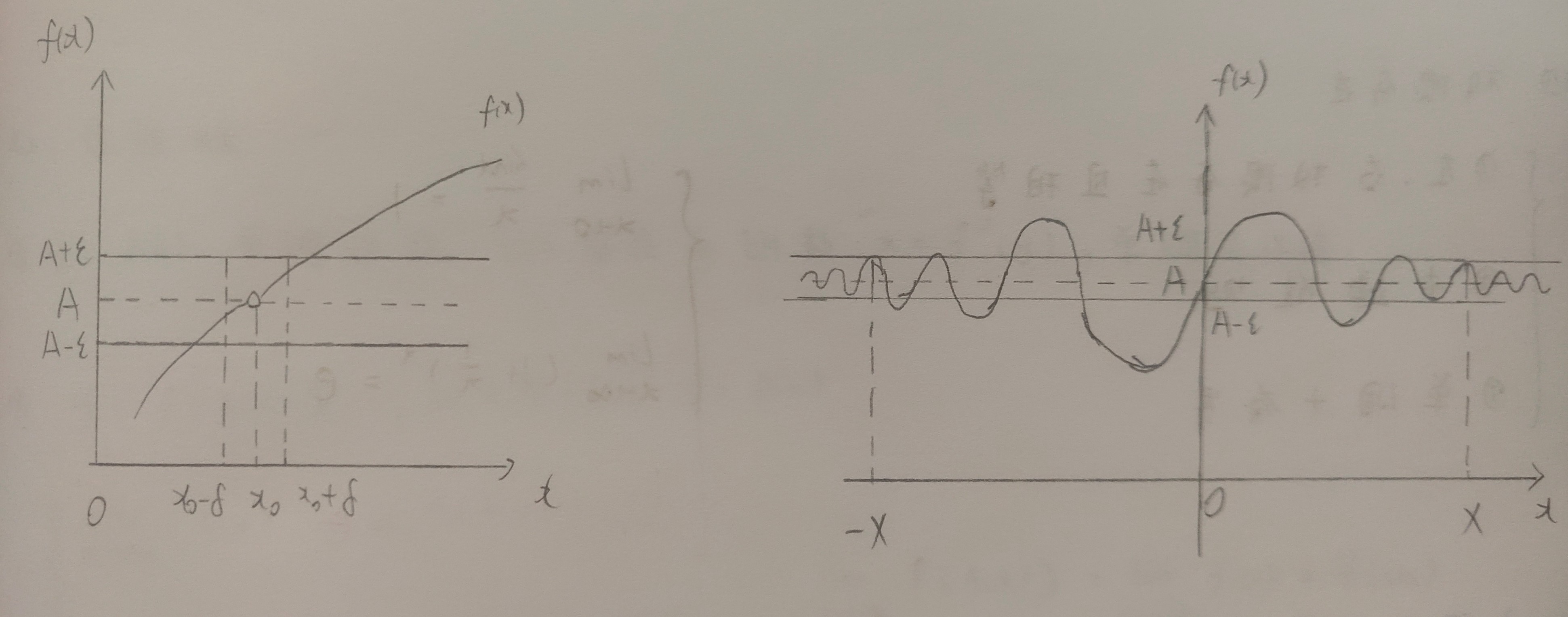
自变量趋于有限值时函数的极限：

\[\lim_{x \to x_0} f(x) = A \iff \forall \epsilon > 0, \exists \delta > 0, 当 0 < |x - x_0| < \delta 时， 有 |f(x) - A| < \epsilon \]

自变量趋于无穷大时函数的极限：

\[\lim_{x \to \infty } f(x) = A \iff \forall \epsilon > 0, \exists X> 0, 当 |x|>X时， 有 |f(x) - A| < \epsilon \]

极限性质

函数极限三大性质:

• 唯一性
• 局部有界性
• 局部保号性

无穷大、无穷小

无穷小

如果函数\(f(x)\)当\(x \to x_0\)(或\(x \to \infty\))时的极限为零，那么称函数\(f(x)\)为当\(x \to x_0\)(或\(x \to \infty\))时的无穷小

无穷小与函数极限的关系：(去极限符号)

在自变量的同一变化过程\(x \to x_0(或x \to \infty)\)中，函数\(f(x)\)具有极限A的充分必要条件是\(f(x) = A + \alpha\) , 其中\(\alpha\)是无穷小

\[\lim_{x \to x_0}f(x) = A \iff f(x) = A + \alpha , \alpha为x \to x_0的无穷小 \]

无穷大

设函数\(f(x)\)在\(x_0\)的某一去心邻域内有定义(或\(|x|\)大于某一正数时有定义). 如果对于任意给定的正数\(M\)(不论它多么大)， 总存在正数\(\delta\)(或正数\(X\))，只要\(x\)适合不等式\(0<|x - x_0| < \delta\)(或\(|x| > X\)), 对应的函数值\(f(x)\)总满足不等式

​ \(|f(x)| > M\)

则称函数\(f(x)\)为当\(x \to x_0(或 x \to \infty)\)时的无穷大

\[\lim_{x \to x_0} f(x) = \infty (或 \lim_{x \to \infty} f(x) = \infty) \]

无穷大与无穷小的关系：

在自变量的同一变化过程中，如果\(f(x)\)为无穷大，则\(\frac{1}{f(x)}\)为无穷小；反之，如果\(f(x)\)为无穷小，且\(f(x)\neq 0\), 则\(\frac{1}{f(x)}\)为无穷大

极限运算法则

定理1

有限个无穷小的和也是无穷小

定理2

有界函数与无穷小的乘积是无穷小

定理3

如果\(\lim f(x)=A, \lim g(x) = B\), 那么

(1) \(\lim [f(x) \pm g(x)] = \lim f(x) \pm \lim g(x) = A \pm B\)

(2) \(\lim [f(x) \cdot g(x)] = \lim f(x) \cdot \lim g(x) = A \cdot B\)

(3) 若又有\(B\neq 0\), 则

​ $$\lim \frac{f(x)}{g(x)}= \frac{\lim f(x)}{\lim g(x)} = \frac{A}{B}$$

定理4