js版九宫格拼图与启发式搜索（A*算法）

　　九宫格拼图游戏大家都很熟悉，这里给大家如介绍何应用状态空间搜索的方式求解拼图的最佳路径和一个游戏dome及自动求解方法；

本文分web版游戏的实现和启发式搜索算法两部分；

先看dome，直接鼠标点击要移动的方块开始游戏，点击 提示 开始最佳路径搜索（启发式）直到最后一步；

（如果提示无解，则表示没有找到最佳路点击重置重新试一次，可通过console查看全部搜索的每一步节点状态，或在js/main.js中打断点看每一步结果，详细内容见下文）

项目地址：https://github.com/pangyongsheng/puzzle

dome演示：http://pangyongsheng.github.io/puzzle/

 

 一、游戏的实现方法

　　首先我们考虑如何用数据表示拼图游戏的状态，即将拼图游戏视图与数据绑定；

　　如下图所示：

　　　　

　　（1）以左上角为原点，建立坐标系，蓝色数字表示位置序号，

　　　　  则该位置div(拼图块）的left和right（向左和向下的偏移距离）等于为其左上角绿点的坐标(x,y)，即：

　　　　　　left    =  x * 小方块边长

　　　　　　right =   y* 小方块边长

 

　　（2）这样的话，我们就可以用一个长度为9数组表示当前拼图的状态空间，

　　　　  如 [2,0,1,5,4,6,7,8,3] 可表示 一号方块在2号位置，二号方块在0号位置...    如下图所示：

                 

 

　　　　　　自此我们就实现了视图与数据的对应关系，把拼图问题转化成为一个数组排列组合问题；

　　（3）对于任意号位置a的坐标c我们可通过建立一个如下二维数组来获取，　

　　　　　　var place= [ 
　　　　　　　　[0, 0],[1, 0],[2, 0],

　　　　　　　　[0, 1],[1, 1],[2, 1],　　　

　　　　　　　　[0, 2],[1, 2],[2, 2]

　　　　　　]

 

　　　　位置序号与坐标则有如下关系

　　　　　　c=place[a]

　　　  由以上可知获取a坐标方法

　　　　

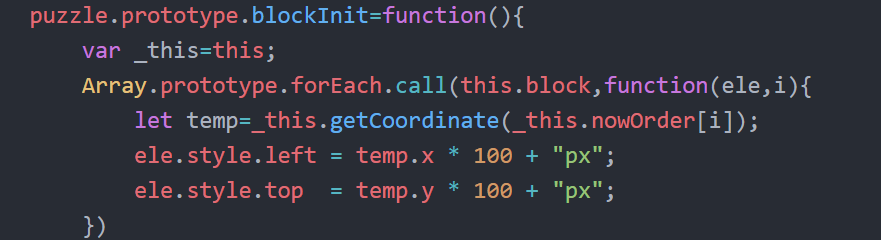
　　　初始化每一个小方块位置方法（block为全部小方块dom,这里借用数组方法forEach遍历div）

　　　　

　　　（4）对于任意两个坐标的距离我们可以表示为

　　　　　　d=| x1 - x2 | +  | y1-y2 |

　　　　　代码如下

　　　　

 　　（5）那么我们可以求得当前状态和目标状态的全部距离为，（每个小方块距离目标的距离求和）,f(x)第x方块距离目标位置的距离

　　　　

　　　　代码如下

　　　　

 　　（6）如何判断点击的方块是否能移动，首先我们将最后一个方块隐藏，如果点击的方块距离最后（8号）方块距离为1则表示可以移动，及两个状态可以转化，

　　　　　这个方法也可以看做两个状态的数组能否相互转化，可作为后面启发式搜索判断节点扩展的方法；

 　　　　

　　　　以上代码为每个方块添加点击事件

 　　　　至此游戏的基本实现方式介绍完毕，详细看代码

 二、启发式搜索

　　启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估，得到最好的位置，再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路径，提高了效率。在启发式搜索中，对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。 

它把到达节点的耗散g(n)和从该节点到目标节点的消耗h(n)结合起来对节点进行评价：f(n)=g(n)+h(n) 

　　简单的说就是扩展当前状态节点的所有可能下一步节点，通过一个方式来估算那个节点最快能到到目标，不断重复知道实现达到目标状态；

　　我们这里的估计方法为 当前状态的全部距离+走的步数；

　　

　　搜索过程可能描述如下：

（1）把初始节点S0放入Open表中，f(S0)=g(S0)+h(S0)；

（2）如果Open表为空，则问题无解，失败退出；

（3）把Open表的第一个节点取出放入Closed表，并记该节点为n；

（4）考察节点n是否为目标节点。若是，则找到了问题的解，成功退出；

（5）若节点n不可扩展，则转到第(2)步；

（6）扩展节点n，生成子节点ni(i=1,2,……)，计算每一个子节点的估价值f(ni) (i=1,2,……)，并为每一个子节点设置指向父节点的指针，然后将这些子节点放入Open表中；

（7）根据各节点的估价函数值，对Open表中的全部节点按从小到大的顺序重新进行排序；

（8）转第(2)步。

　　代码太长 截图不够，详细还是看代码吧：O(∩_∩)O

　　

　　

　　我是把一步的搜索结果直接展示在视图中的，所以closed表中没有保留节点状态，单通过console.log输出，大家可以点击F12在调试模式下查看全部节点；

　　若希望查看每一步视图状态，则可以在searchA方法的while循环中打断点查看效果；

 

 　　

 　　网上找个图说明一下搜索的方法：容易明白

　　

          

 

 

 

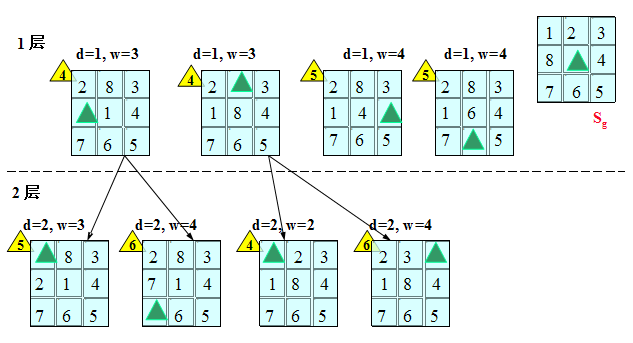
 其实这里还是有个两问题需注意:

（1）并不是每次都能找到目标状态 ，因为我的数组打乱是完全随机的，而寻路的限制是只能两个相邻节点互换位置；

（2）在每次扩展节点的时候需考虑这个节点是否已经出现在closed表中（即寻路的过程中出现过改节点），这样会导致寻路的过程在几个节点中转圈，陷入死循环； 但也不能完全限制closed的表中的数据不能重复出现，这样会降低寻路成功的可能性；这里我取了一个比较合理的值256,即在最近的256次中没有出现过改节点；