数据结构之二叉树遍历与深度计算
刚刚辞职交接完毕,话说有家公司给我打了n次电话想让我去,但是薪水问题没有谈拢,薪水不低,但是没达到我的期望,开发的项目俺还是蛮喜欢的,可惜了~~~~~
准备找新工作中,想起好多公司有考数据结构的习惯,于是复习了下,链表比较简单,一会翻看完了。但是二叉树这里让我稍稍郁闷了下。
二叉树的遍历是基础,包括先序遍历,中序遍历和后续遍历。自己写了程序才发现好多知识都不记得了,才发现原来三种遍历都是同样的算法,不同在于操作节点的位置不同,代码是递归的,等有时间再写非递归的吧。
要想遍历二叉树必须有先初始化一个二叉树,以下是代码,不必多说,比C看起来容易理解多了,首先是Node类(节点),这个可是基础呃~~~
采用递归方式写一个方法,需求如下:
遍历二叉树的话首先要传入根节点
1)如果节点为空则返回
2)如果节点不为空,调用方法本身分别遍历左子树和右子树。
3)先序遍历在传入的node后并且node不为空时操作(本例中是输出node的Value值)。
判断node是否为空
Do operation here.
遍历左子树
遍历右子树
4)中序遍历在遍历左子树后操作。
判断node是否为空
遍历左子树
Do operation here.
遍历右子树
5)后序遍历在遍历右子树后操作。
判断node是否为空
遍历左子树
遍历右子树
Do operation here.
还是看代码吧,有的时候代码比描述更重要,吼吼~~~~
怎么获得二叉树的深度那,这个有点麻烦了,不是一下就可以看出来的,不过对于递归方法来说有个原则是百试不爽的,那就是把具体问题抽象成“数学公式”。有一个基本规律,那就是下层深度是其上层深度+1。(智商没问题的都应该清楚吧,呵呵~~~~~)
1)同样使用递归,首先判断node是否为null,如果是null返回0,也就是说二叉树是空的,深度为0。
2)如果左子树为空,右子树不为空,也就是说该节点有下层,而下层深度是该深度+1。
3)如果左子树不为空,右子树为空,同样该节点有下层,而下层深度是该深度+1。
4)如果左子树不为空,右子树也不为空,那么就需要比较左子树和右子树的深度,哪个深度大取哪个。
抽象成数学公式为:
GetDeep(node.RightChildNode) + 1 (node.LeftChildNode == null && node.RightChildNode != null)
GetDeep(Node node)= { GetDeep(node.LeftChildNode) + 1 (node.LeftChildNode != null && node.RightChildNode == null)
Max(GetDeep(node.LeftChildNode),GetDeep(node.RightChildNode)) + 1
(node.LeftChildNode != null && node.RightChildNode != null)
1 (其他情况)
具体代码如下:
经过分析后发现条件判断有写罗嗦了,实际可以合并,合并后的GetDeep方法如下:
准备找新工作中,想起好多公司有考数据结构的习惯,于是复习了下,链表比较简单,一会翻看完了。但是二叉树这里让我稍稍郁闷了下。
二叉树的遍历是基础,包括先序遍历,中序遍历和后续遍历。自己写了程序才发现好多知识都不记得了,才发现原来三种遍历都是同样的算法,不同在于操作节点的位置不同,代码是递归的,等有时间再写非递归的吧。
要想遍历二叉树必须有先初始化一个二叉树,以下是代码,不必多说,比C看起来容易理解多了,首先是Node类(节点),这个可是基础呃~~~
class Node
{
private Node _leftChildNode;//左子树
private Node _rightChildNode;//右子树
private string _vlaue;//节点值
public Node LeftChildNode
{
get { return _leftChildNode; }
set { _leftChildNode = value; }
}
public Node RightChildNode
{
get { return _rightChildNode; }
set { _rightChildNode = value; }
}
public string Value
{
get { return _vlaue; }
}
public Node(string value)
{
_vlaue = value;
}
}
有了节点就来初始化二叉树吧。go go go~~{
private Node _leftChildNode;//左子树
private Node _rightChildNode;//右子树
private string _vlaue;//节点值
public Node LeftChildNode
{
get { return _leftChildNode; }
set { _leftChildNode = value; }
}
public Node RightChildNode
{
get { return _rightChildNode; }
set { _rightChildNode = value; }
}
public string Value
{
get { return _vlaue; }
}
public Node(string value)
{
_vlaue = value;
}
}
static void InitBinaryTree(Node root)
{
Node nodePlus = new Node("+");
Node nodeMod = new Node("/");
Node nodeA = new Node("a");
Node nodeMultiply = new Node("*");
Node nodeE = new Node("e");
Node nodeF = new Node("f");
Node nodeB = new Node("b");
Node nodeSub = new Node("-");
Node nodeC = new Node("c");
Node nodeD = new Node("d");
root.LeftChildNode = nodePlus;
root.RightChildNode = nodeMod;
nodePlus.LeftChildNode = nodeA;
nodePlus.RightChildNode = nodeMultiply;
nodeMod.LeftChildNode = nodeE;
nodeMod.RightChildNode = nodeF;
nodeMultiply.LeftChildNode = nodeB;
nodeMultiply.RightChildNode = nodeSub;
nodeSub.LeftChildNode = nodeC;
nodeSub.RightChildNode = nodeD;
}
OK,数据源有了,现在就来上主菜,遍历二叉树喽~{
Node nodePlus = new Node("+");
Node nodeMod = new Node("/");
Node nodeA = new Node("a");
Node nodeMultiply = new Node("*");
Node nodeE = new Node("e");
Node nodeF = new Node("f");
Node nodeB = new Node("b");
Node nodeSub = new Node("-");
Node nodeC = new Node("c");
Node nodeD = new Node("d");
root.LeftChildNode = nodePlus;
root.RightChildNode = nodeMod;
nodePlus.LeftChildNode = nodeA;
nodePlus.RightChildNode = nodeMultiply;
nodeMod.LeftChildNode = nodeE;
nodeMod.RightChildNode = nodeF;
nodeMultiply.LeftChildNode = nodeB;
nodeMultiply.RightChildNode = nodeSub;
nodeSub.LeftChildNode = nodeC;
nodeSub.RightChildNode = nodeD;
}
采用递归方式写一个方法,需求如下:
遍历二叉树的话首先要传入根节点
1)如果节点为空则返回
2)如果节点不为空,调用方法本身分别遍历左子树和右子树。
3)先序遍历在传入的node后并且node不为空时操作(本例中是输出node的Value值)。
判断node是否为空
Do operation here.
遍历左子树
遍历右子树
4)中序遍历在遍历左子树后操作。
判断node是否为空
遍历左子树
Do operation here.
遍历右子树
5)后序遍历在遍历右子树后操作。
判断node是否为空
遍历左子树
遍历右子树
Do operation here.
还是看代码吧,有的时候代码比描述更重要,吼吼~~~~
static void TraversalBinaryTree(Node node, TraversalType traversalType)
{
if (node != null)
{
if (traversalType == TraversalType.TT_First)
{
Console.WriteLine(node.Value);
}
TraversalBinaryTree(node.LeftChildNode, traversalType);
if (traversalType == TraversalType.TT_Middle)
{
Console.WriteLine(node.Value);
}
TraversalBinaryTree(node.RightChildNode, traversalType);
if (traversalType == TraversalType.TT_Last)
{
Console.WriteLine(node.Value);
}
return;
}
else
{
return;
}
}
方法的参数有些特殊,除了Node外还有个TraversalType,这个就是我们三种遍历方式的标志了,同样按照惯例被声明为了enum类型。{
if (node != null)
{
if (traversalType == TraversalType.TT_First)
{
Console.WriteLine(node.Value);
}
TraversalBinaryTree(node.LeftChildNode, traversalType);
if (traversalType == TraversalType.TT_Middle)
{
Console.WriteLine(node.Value);
}
TraversalBinaryTree(node.RightChildNode, traversalType);
if (traversalType == TraversalType.TT_Last)
{
Console.WriteLine(node.Value);
}
return;
}
else
{
return;
}
}
enum TraversalType
{
TT_First = 1, TT_Middle, TT_Last
}
OK,二叉树的遍历代码完成,剩下的就需要写测试代码了,别急,我们还有获得二叉树深度的方法没写那,放在一起测试吧,呵呵。{
TT_First = 1, TT_Middle, TT_Last
}
怎么获得二叉树的深度那,这个有点麻烦了,不是一下就可以看出来的,不过对于递归方法来说有个原则是百试不爽的,那就是把具体问题抽象成“数学公式”。有一个基本规律,那就是下层深度是其上层深度+1。(智商没问题的都应该清楚吧,呵呵~~~~~)
1)同样使用递归,首先判断node是否为null,如果是null返回0,也就是说二叉树是空的,深度为0。
2)如果左子树为空,右子树不为空,也就是说该节点有下层,而下层深度是该深度+1。
3)如果左子树不为空,右子树为空,同样该节点有下层,而下层深度是该深度+1。
4)如果左子树不为空,右子树也不为空,那么就需要比较左子树和右子树的深度,哪个深度大取哪个。
抽象成数学公式为:
GetDeep(node.RightChildNode) + 1 (node.LeftChildNode == null && node.RightChildNode != null)
GetDeep(Node node)= { GetDeep(node.LeftChildNode) + 1 (node.LeftChildNode != null && node.RightChildNode == null)
Max(GetDeep(node.LeftChildNode),GetDeep(node.RightChildNode)) + 1
(node.LeftChildNode != null && node.RightChildNode != null)
1 (其他情况)
具体代码如下:
static int GetDeep(Node node)
{
if (node != null)
{
if (node.LeftChildNode == null && node.RightChildNode != null)
{
return GetDeep(node.RightChildNode) + 1;
}
else if (node.LeftChildNode != null && node.RightChildNode == null)
{
return GetDeep(node.LeftChildNode) + 1;
}
else if (node.LeftChildNode != null && node.RightChildNode != null)
{
int left = GetDeep(node.LeftChildNode);
int right = GetDeep(node.RightChildNode);
return (left > right ? left : right) + 1;
}
else
{
return 1;
}
}
else
{
return 0;
}
}
OK,到这里我们需要的东西都完成了,下面就该测试了,下面是完整代码:{
if (node != null)
{
if (node.LeftChildNode == null && node.RightChildNode != null)
{
return GetDeep(node.RightChildNode) + 1;
}
else if (node.LeftChildNode != null && node.RightChildNode == null)
{
return GetDeep(node.LeftChildNode) + 1;
}
else if (node.LeftChildNode != null && node.RightChildNode != null)
{
int left = GetDeep(node.LeftChildNode);
int right = GetDeep(node.RightChildNode);
return (left > right ? left : right) + 1;
}
else
{
return 1;
}
}
else
{
return 0;
}
}
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Runtime.InteropServices;
namespace BinaryTree
{
class Program
{
static int left = 0;
static int right = 0;
static void Main(string[] args)
{
Node root = new Node("#");
InitBinaryTree(root);
do
{
Console.WriteLine();
Console.WriteLine("Please input the type of Tranversal.\n1:First\n2:Middle\n3:Last");
string input = Console.ReadLine();
int travertalType;
if (int.TryParse(input, out travertalType))
{
TraversalBinaryTree(root, (TraversalType)travertalType);
int deep = GetDeep(root);
Console.WriteLine(String.Format("Deep is {0}.", deep));
Console.WriteLine("OK,press any key to continue.\nEsc:Quit");
}
else
{
Console.WriteLine("Input Error.press any key to continue.\nEsc:Quit");
}
} while (Console.ReadKey().Key != ConsoleKey.Escape);
}
static void InitBinaryTree(Node root)
{
Node nodePlus = new Node("+");
Node nodeMod = new Node("/");
Node nodeA = new Node("a");
Node nodeMultiply = new Node("*");
Node nodeE = new Node("e");
Node nodeF = new Node("f");
Node nodeB = new Node("b");
Node nodeSub = new Node("-");
Node nodeC = new Node("c");
Node nodeD = new Node("d");
root.LeftChildNode = nodePlus;
root.RightChildNode = nodeMod;
nodePlus.LeftChildNode = nodeA;
nodePlus.RightChildNode = nodeMultiply;
nodeMod.LeftChildNode = nodeE;
nodeMod.RightChildNode = nodeF;
nodeMultiply.LeftChildNode = nodeB;
nodeMultiply.RightChildNode = nodeSub;
nodeSub.LeftChildNode = nodeC;
nodeSub.RightChildNode = nodeD;
}
static void TraversalBinaryTree(Node node, TraversalType traversalType)
{
if (node != null)
{
if (traversalType == TraversalType.TT_First)
{
Console.WriteLine(node.Value);
}
TraversalBinaryTree(node.LeftChildNode, traversalType);
if (traversalType == TraversalType.TT_Middle)
{
Console.WriteLine(node.Value);
}
TraversalBinaryTree(node.RightChildNode, traversalType);
if (traversalType == TraversalType.TT_Last)
{
Console.WriteLine(node.Value);
}
return;
}
else
{
return;
}
}
static int GetDeep(Node node)
{
if (node != null)
{
if (node.LeftChildNode == null && node.RightChildNode != null)
{
return GetDeep(node.RightChildNode) + 1;
}
else if (node.LeftChildNode != null && node.RightChildNode == null)
{
return GetDeep(node.LeftChildNode) + 1;
}
else if (node.LeftChildNode != null && node.RightChildNode != null)
{
int left = GetDeep(node.LeftChildNode);
int right = GetDeep(node.RightChildNode);
return (left > right ? left : right) + 1;
}
else
{
return 1;
}
}
else
{
return 0;
}
}
enum TraversalType
{
TT_First = 1, TT_Middle, TT_Last
}
}
class Node
{
private Node _leftChildNode;
private Node _rightChildNode;
private string _vlaue;
public Node LeftChildNode
{
get { return _leftChildNode; }
set { _leftChildNode = value; }
}
public Node RightChildNode
{
get { return _rightChildNode; }
set { _rightChildNode = value; }
}
public string Value
{
get { return _vlaue; }
}
public Node(string value)
{
_vlaue = value;
}
}
}
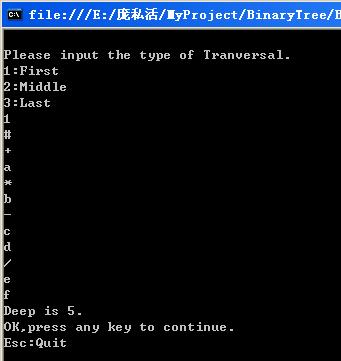
测试结果如下:)using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Runtime.InteropServices;
namespace BinaryTree
{
class Program
{
static int left = 0;
static int right = 0;
static void Main(string[] args)
{
Node root = new Node("#");
InitBinaryTree(root);
do
{
Console.WriteLine();
Console.WriteLine("Please input the type of Tranversal.\n1:First\n2:Middle\n3:Last");
string input = Console.ReadLine();
int travertalType;
if (int.TryParse(input, out travertalType))
{
TraversalBinaryTree(root, (TraversalType)travertalType);
int deep = GetDeep(root);
Console.WriteLine(String.Format("Deep is {0}.", deep));
Console.WriteLine("OK,press any key to continue.\nEsc:Quit");
}
else
{
Console.WriteLine("Input Error.press any key to continue.\nEsc:Quit");
}
} while (Console.ReadKey().Key != ConsoleKey.Escape);
}
static void InitBinaryTree(Node root)
{
Node nodePlus = new Node("+");
Node nodeMod = new Node("/");
Node nodeA = new Node("a");
Node nodeMultiply = new Node("*");
Node nodeE = new Node("e");
Node nodeF = new Node("f");
Node nodeB = new Node("b");
Node nodeSub = new Node("-");
Node nodeC = new Node("c");
Node nodeD = new Node("d");
root.LeftChildNode = nodePlus;
root.RightChildNode = nodeMod;
nodePlus.LeftChildNode = nodeA;
nodePlus.RightChildNode = nodeMultiply;
nodeMod.LeftChildNode = nodeE;
nodeMod.RightChildNode = nodeF;
nodeMultiply.LeftChildNode = nodeB;
nodeMultiply.RightChildNode = nodeSub;
nodeSub.LeftChildNode = nodeC;
nodeSub.RightChildNode = nodeD;
}
static void TraversalBinaryTree(Node node, TraversalType traversalType)
{
if (node != null)
{
if (traversalType == TraversalType.TT_First)
{
Console.WriteLine(node.Value);
}
TraversalBinaryTree(node.LeftChildNode, traversalType);
if (traversalType == TraversalType.TT_Middle)
{
Console.WriteLine(node.Value);
}
TraversalBinaryTree(node.RightChildNode, traversalType);
if (traversalType == TraversalType.TT_Last)
{
Console.WriteLine(node.Value);
}
return;
}
else
{
return;
}
}
static int GetDeep(Node node)
{
if (node != null)
{
if (node.LeftChildNode == null && node.RightChildNode != null)
{
return GetDeep(node.RightChildNode) + 1;
}
else if (node.LeftChildNode != null && node.RightChildNode == null)
{
return GetDeep(node.LeftChildNode) + 1;
}
else if (node.LeftChildNode != null && node.RightChildNode != null)
{
int left = GetDeep(node.LeftChildNode);
int right = GetDeep(node.RightChildNode);
return (left > right ? left : right) + 1;
}
else
{
return 1;
}
}
else
{
return 0;
}
}
enum TraversalType
{
TT_First = 1, TT_Middle, TT_Last
}
}
class Node
{
private Node _leftChildNode;
private Node _rightChildNode;
private string _vlaue;
public Node LeftChildNode
{
get { return _leftChildNode; }
set { _leftChildNode = value; }
}
public Node RightChildNode
{
get { return _rightChildNode; }
set { _rightChildNode = value; }
}
public string Value
{
get { return _vlaue; }
}
public Node(string value)
{
_vlaue = value;
}
}
}

经过分析后发现条件判断有写罗嗦了,实际可以合并,合并后的GetDeep方法如下:
static int GetDeep(Node node)
{
if (node != null)
{
//if (node.LeftChildNode != null && node.RightChildNode == null)
//{
// return GetDeep(node.LeftChildNode) + 1;
//}
//else if (node.RightChildNode != null && node.LeftChildNode == null)
//{
// return GetDeep(node.RightChildNode) + 1;
//}
//else if (node.RightChildNode != null && node.LeftChildNode != null)
//{
// int left = GetDeep(node.LeftChildNode);
// int right = GetDeep(node.RightChildNode);
// return (left > right ? left : right) + 1;
//}
//else
//{
// return 1;
//}
int left = GetDeep(node.LeftChildNode);
int right = GetDeep(node.RightChildNode);
return (left > right ? left : right) + 1;
}
else
{
return 0;
}
}
{
if (node != null)
{
//if (node.LeftChildNode != null && node.RightChildNode == null)
//{
// return GetDeep(node.LeftChildNode) + 1;
//}
//else if (node.RightChildNode != null && node.LeftChildNode == null)
//{
// return GetDeep(node.RightChildNode) + 1;
//}
//else if (node.RightChildNode != null && node.LeftChildNode != null)
//{
// int left = GetDeep(node.LeftChildNode);
// int right = GetDeep(node.RightChildNode);
// return (left > right ? left : right) + 1;
//}
//else
//{
// return 1;
//}
int left = GetDeep(node.LeftChildNode);
int right = GetDeep(node.RightChildNode);
return (left > right ? left : right) + 1;
}
else
{
return 0;
}
}





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· .NET周刊【3月第1期 2025-03-02】
· 分享 3 个 .NET 开源的文件压缩处理库,助力快速实现文件压缩解压功能!
· Ollama——大语言模型本地部署的极速利器