几种内部排序-分类-复杂性-稳定性

1. 简述

    本文主要说明一些常用的内部排序算法的分类、复杂性和稳定性。主要基于现在的理解和学习，详细准确的复杂度可以参见维基百科等比较权威的网站，对于一些算法的不同实现，复杂度也不同，这里给出的复杂度都是相对较好的算法的复杂度。

2. 分类
   

3. 复杂性和稳定性

    

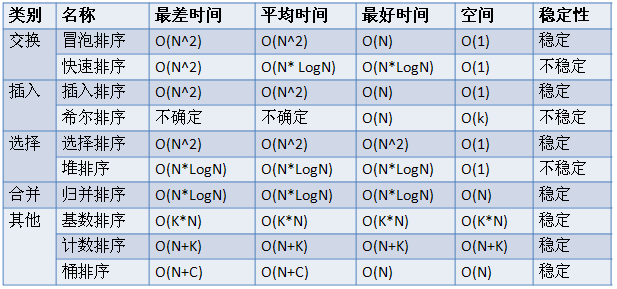
    冒泡排序：在已经有序的情况，取得O(N)的复杂度。
    快速排序：每次递归都是N的复杂度，递归次数根据序列有关系，当已经有序的情况下，递归N次，时间复杂度为O(N*LogN)
    插入排序：在已经有序的情况，取得O(N)的复杂度。
    希尔排序：最差时间和平均时间都要根据步长数组来判断，现在最好算法的最差时间复杂度，为O(N*LogN)。空间主要是步长数组需要的。一般步长之间不要存在公因子。
    插入排序：交换次数比冒泡排序少多了，由于交换所需CPU时间比比较所需的CPU时间多，n值较小时，选择排序比冒泡排序快。
    堆排序：  堆排序属于选择排序，选择N-1次，每次从堆中选择一个，因此最差就是N*LogN。最好的时间无法准确估计，基本上也是N*LogN这个程度。
    归并排序：这个排序算法的复杂度与数组初始化序列无关，归并次数为LogN次，每次复杂度是O(N)，因此复杂度都是O(N*LogN)
    基数排序：K是数组中，数值的最大位数。对于int来说，使用十进制的话，K<=10。稳定性来说，基数排序要求每次必须使用稳定排序，否则最终得不到正确结果。所以这里的稳定是必须的，而不可能存在不稳定的。而其他的排序，比如冒泡排序，可以改写成不稳定的，这点需要注意。
    计数排序：K是数组中，数值的范围，即K=Max-Min+1。对于int来说，最坏的情况为K=2^32，即数组内包含了最大正数和最小负数。
    桶排序：由于桶排序可能有的桶没有数据，那么假设N个数据，只被分到了M个桶中，O(N)+O(M*(N/M)*log(N/M))=O(N+N*(logN-logM))=O(N+N*logN-N*logM) =O(N+N*(logN-logM))，当分到的桶越多时，越是接近N。计数排序可以看作桶排序的一个特例，将桶开的很大，直到能够保证每个不同的数值都被分到一个桶中。

4. 参考

    维基百科
    三种线性排序算法 计数排序、桶排序与基数排序    http://www.byvoid.com/blog/sort-radix/
    桶排序与基排序    http://anwj336.blog.163.com/blog/static/8941520920109535025216/