NKPC7-2154-Birds Attack
1. 概述
这道题,仔细讨论增减性还是比较复杂,我分情况在不同的范围上,使用三分法,实际上,直接使用三分法就可以AC。
2. 分析
假设水平速度为V1,垂直速度为V2。
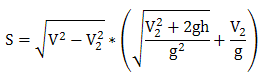
由于V2的取值范围是[0, V],因此等式右边第一个部分是单调递减,由于是凸的二次函数,递减速度越来越快,等式右边第二个部分是单调递增,由于是凹的二次函数,递增的速度越来越慢。两个函数相乘的话有可能会产生一个先上升后下降的趋势。
这样分析,还没有足够说服力,实际上,右边第二个部分分开乘出来,然后转变为两个曲线的加法,再根据中心线的位置判断S的增减性更加清楚。不过这道题,三分法就过了,还是主要给出三分法的伪代码。
3. 三分法
以前不知道什么是三分法,做这道题的时候,想到寻找一个凸函数最大值的方法,后来在网上搜索了一下,和自己给出的方法是一样的,还有点小开心。
已知:凸函数的值计算的函数原型为int Value(int ), 定义域范围是[0, V]
Left = 0,Right = V;
While(fabs(Right-Left)>1e-6 ||
fabs(Value(Right)-Value(Left))>1e-10)
{
Tmp1 = Left + (Right-Left)/3;
Tmp2 = Left + (Right-Left)*2/3;
if(Tmp1<Tmp2) Left = Tmp1;
else Right = Tmp2;
}
While(fabs(Right-Left)>1e-6 ||
fabs(Value(Right)-Value(Left))>1e-10)
{
Tmp1 = Left + (Right-Left)/3;
Tmp2 = Left + (Right-Left)*2/3;
if(Tmp1<Tmp2) Left = Tmp1;
else Right = Tmp2;
}
当Tmp1<Tmp2时,说明Tmp1肯定是在最大值的左边,因此更新Left。反之,说明,Tmp2肯定是在最大值的右边,因此更新Right。
4. 题目网址





