NKPC7-2153-All Star Game
1. 概述
这是NKPC7中的第一道题目,虽然AC了,但是后来发现方法是有问题的,主要是数据还不够严谨。另外,同学给出的一个贪心方法,经过一番思考也发现了问题。标准答案是枚举+判断,因此,这里主要总结走过的一些弯路。
2. 错误的AC方法
顶点就是队伍,边是队伍的共存关系,如果两个队伍能够共存,则存在边,否则不存在边。最多能够共存的队伍就是最多的相互之间有边直接到达的顶点集合。
首先,从每个顶点分别开始计算最大共存队伍数。在每次计算的时候,依次遍历其他的队伍,如果能够与已有队伍共存就加入进来。
其次,选取前面得到的N个最大共存队伍数量的最大值,即为所得。
反例:
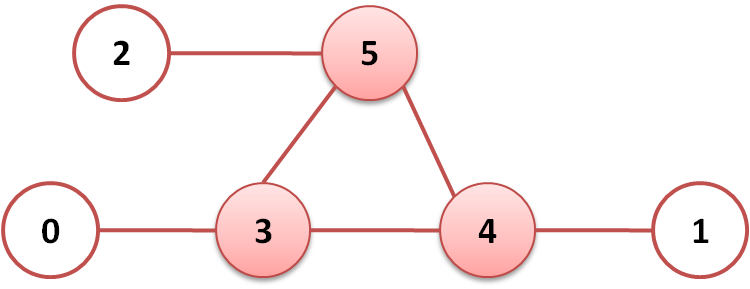
最大共存队伍是3,4,5。
起始节点为0:{0,3},起始节点为1:{1,4},起始节点为2:{2,5}
起始节点为3:{3,0},起始节点为4:{4,1},起始节点为5:{5,2}
当起始节点为3时,由于先检查0号节点,发现可以共存,但是4和5都不能与0共存。因此,该方法得到的结果不是最优的。
题目侥幸AC是由于在指定起始节点后,遍历其他节点时,从后向前遍历,而数据不够严谨。后来我重新程序,从前向后遍历,结果3个WA,才发现了问题。
3. 错误的贪心方法
同学给出的。建图方式和前面的正好相反:如果两个队伍之间有相同的队员(即不能共存)时,则存在边。目标是通过合理的删除一些顶点,得到最多的没有边的顶点集合。
方法是每次删除度最大的节点,更新图,再删除度最大的节点,直到图中不再有边为止。
伪码: while(图中边数>0) {
删除度最大的节点
更新图
}
反例:
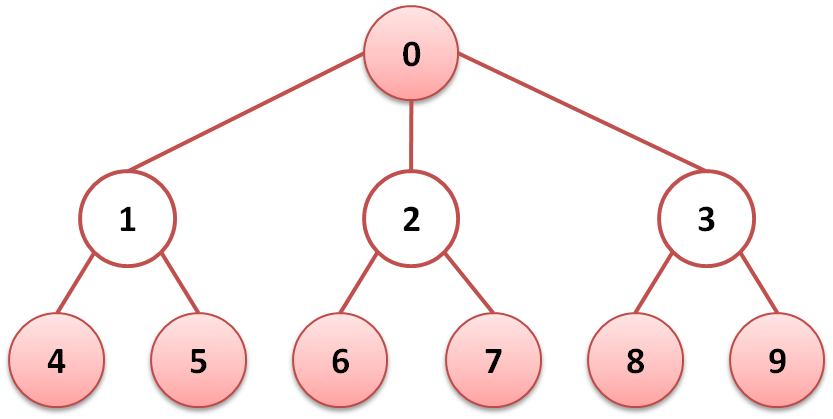
最大共存队伍:{0,4,5,6,7,8,9},但是由于0,1,2,3的度都是3,开始可能先删除0号节点,如果先删除0号节点,那么,最后,只能得到{4,5,6,7,8,9},不是最优解。
反例:
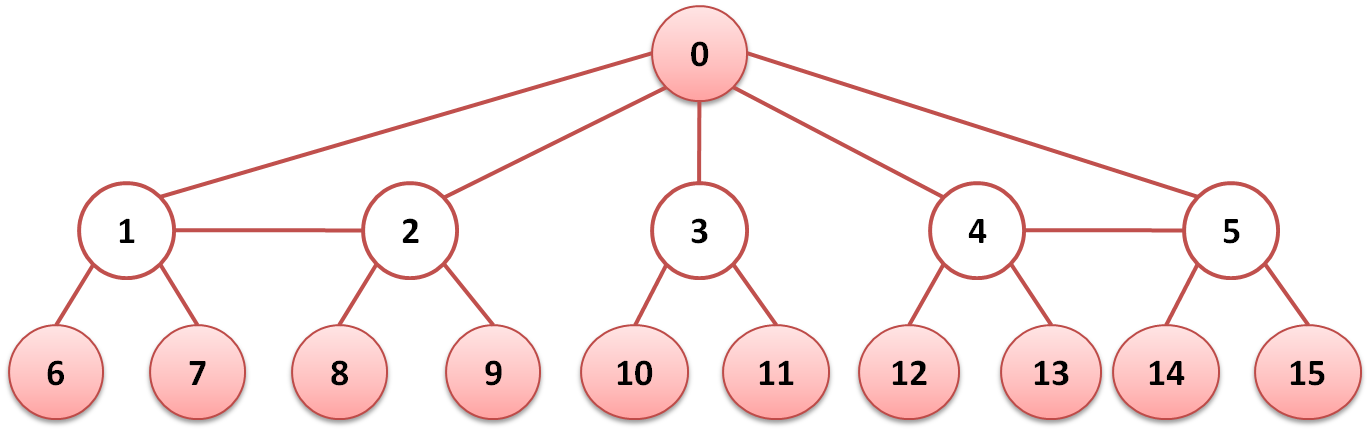
这里,0号节点的初度最大,因此,必然会先删除0号节点。因此方法不能得到最优解。
4. 标准答案
标准答案说明:枚举+判断。N<=20,这样搜索的范围是2^20,大约在10^6的范围,搜索过程剪枝还是相对容易。比如:当前剩余节点都算上也不够的情况。
5. 题目网址





