2022/8/19日测试 (回首向来萧瑟处,归去,也无风雨也无晴 ) (内含Ticket Game,生日蛋糕,最优贸易,装满的油箱,道路游戏)
今天是集训的最后一天,提一首小词送给自己
莫听穿林打叶声,何妨吟啸且徐行。
竹杖芒鞋轻胜马,谁怕?一蓑烟雨任平生。
料峭春风吹酒醒,微冷,山头斜照却相迎。
回首向来萧瑟处,归去,也无风雨也无晴。
Ticket Game
标签:思维

考虑Bob在什么情况下会输。如果他在最后一次填数时两边的差距已经超过了9,Alice就赢了。所以Alice一定想让两端的差距越大越好,Bob一定想让两端平衡。显然,最优策略是Alice在大的那一半拼命加9,Bob在小的那一半拼命加9。
考虑两边的初始值相等并且问号相等的情况,那肯定Bob赢。无论Alice填了什么内容,Bob都可以在相对应的位置填入相同的数字,这样,始终能够保证左右两半的数字之和都是一样的。
如果两端和不相等时,Alice就在大的那一半拼命加9,Bob小的那一半拼命加9。这样一直操作,如果小的那一边没"?"了,Alice肯定赢。如果大的那一边没"?"了,Alice一定会在小的那一边填0,而Bob一定会填9。这样,我们只需要计算Bob在这一半内能填入多少个数字,假设Bob能填 x个数字,那么,如果恰好两边的差为9*x ,则Bob可以获胜,否则,都是Alice获胜。
为什么呢?如果两边的差一开始就大于9*x,那不必说,一定是Alice赢。而如果数字和小的一半加上 9*x 大于了数字和大的一半,那么,Alice可以选择使劲的填入9,这样这一半就会超过想要的大小。但如果两边的差为9*x,无论Alice填什么,Bob都只用填9-Alice填的值即可满足情况
Code
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 5;
int n;
char s[maxn];
int main() {
cin >> n;
cin >> s;
int l = 0, r = 0;
int p = 0, q = 0;
for (int i = 0; i < n / 2; i++) {
if (s[i] != '?') {
l += s[i] - '0';
} else
p++;
}
for (int i = n / 2; i < n; i++) {
if (s[i] != '?') {
r += s[i] - '0';
} else
q++;
}
int tt = min(p, q);
p -= tt;
q -= tt;
if ((p - q) / 2 * 9 == r - l)
cout << "Bob" << endl;
else
cout << "Alice" << endl;
return 0;
}
最优贸易
标签:最短路
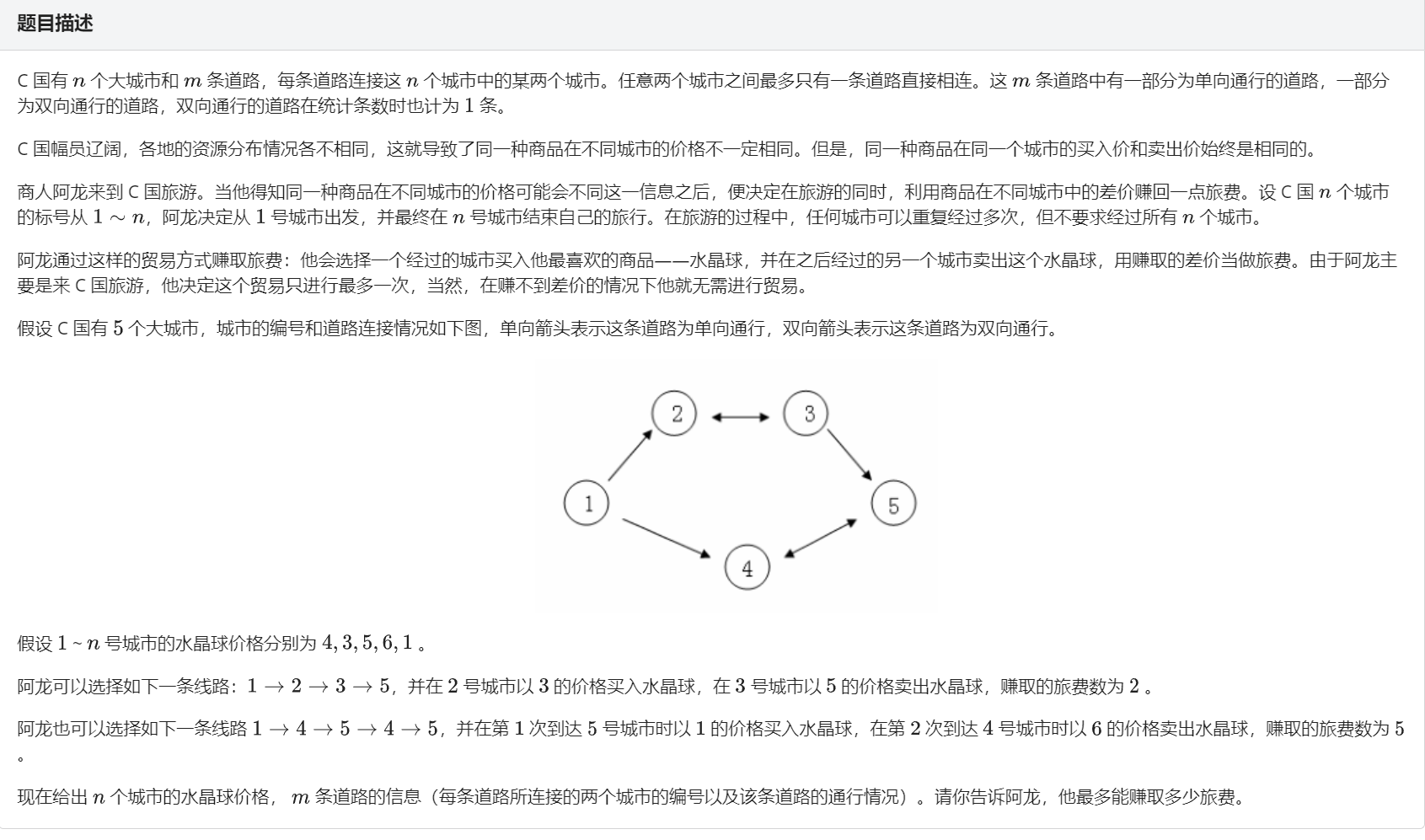
考试的时候想的就是枚举买点和卖点,很显然会超时,只有20pts。
暴力代码如下(20pts)
#include<bits/stdc++.h>
using namespace std;
#define re register
int a[100005],vis[100005];
vector<int> G[500005];
int n,m;
inline bool check(int x,int y) { //判断两点是否联通
queue<int> Q;
while(!Q.empty()) Q.pop();
Q.push(x);
for(re int i=1;i<=n;i++) vis[i]=0;
while(!Q.empty()) {
re int v=Q.front();
Q.pop();
if(v==y) return true;
if(vis[v]) continue;
vis[v]=1;
for(re int i=0;i<G[v].size();i++) {
re int vv=G[v][i];
Q.push(vv);
}
}
return false;
}
int main() {
//freopen("trade.in","r",stdin);
//freopen("trade.out","w",stdout);
n=read(),m=read();
for(re int i=1;i<=n;i++) {
a[i]=read();
}
while(m--) {
re int x,y,z;
x=read(),y=read(),z=read();
if(z==1) {
G[x].push_back(y);
}
else {
G[y].push_back(x);
G[x].push_back(y);
}
}
re int ans=0;
for(re int i=1;i<=n;i++) {
for(re int j=1;j<=n;j++) {
if(a[j]-a[i]<=0) continue;
if(check(i,j)) {
ans=max(ans,a[j]-a[i]);
}
}
}
printf("%d",ans);
return 0;
}
题目本质:在走过的路中,从起点到终点的这条路径上的最小的买入价值点和最大的卖出价值点。
仔细观察可以发现,对于最终的答案而言,我们最终走不走这个点,取决于从1 到这个点i 时价值的最小值与从点i 到点n 路上价值的最大值的价值差。因此,我们可以跑两个SPFA,一个用来求从起点出发,到另外任意一个点的最小值,另一个用来求从终点出发,到其他任意一个点的最大值,最后取所有点最大值与最小值差最大的那个,就是我们的答案。
Q:为什么不用Dijkstra?
A:这道题是可以重复走点的,而Dijkstra的vis数组限制不能重复
SPFA:我和你不熟
附一个SPFA模板
queue<int> Q;
int dis[MAXN+5];
bool vis[MAXN+5];
vector<edge> G[MAXN+5];
int SPFA(int s,int t) {
memset(dis,0x3f,sizeof(dis));
dis[s]=0,vis[s]=1,Q.push(s);
while(!Q.empty()) {
int u=Q.front();
Q.pop();
for(int i=0;i<G[u].size();i++) {
int v=G[u][i].v,w=G[u][i].w;
if(dis[v]>=dis[u]+w) {
dis[v]=dis[u]+w;
if(!vis[v])
vis[v]=1,Q.push(v);
}
}
}
return dis[t];
}给我好好复习
Code
#include<bits/stdc++.h>
using namespace std;
#define N 100002
int n,m,s[N],maxn[N],minn[N],vis[N],v[N],ans;
vector<int> a[N],b[N];
void spfa(int s){
memset(minn,0x3f,sizeof minn);
vis[s]=1;
minn[s]=v[s];
queue<int>que;
que.push(s);
while(!que.empty()) {
int k=que.front();
que.pop();
for(int i=0;i<a[k].size();i++) {
minn[a[k][i]]=min(minn[a[k][i]],min(v[a[k][i]],minn[k]));
if(!vis[a[k][i]]){
vis[a[k][i]]=1;
que.push(a[k][i]);
}
}
}
}
void SPFA(int s){
vis[s]=1;
maxn[s]=v[s];
queue<int>que;
que.push(s);
while(!que.empty()) {
int k=que.front();
que.pop();
for(int i=0;i<b[k].size();i++) {
maxn[b[k][i]]=max(maxn[b[k][i]],max(v[b[k][i]],maxn[k]));
if(!vis[b[k][i]]){
vis[b[k][i]]=1;
que.push(b[k][i]);
}
}
}
}
int main(){
n=read();
m=read();
for(int i=1;i<=n;i++)
v[i]=read();
for(int i=1,x,y,z;i<=m;i++){
x=read();y=read();z=read();
if(z==1)
a[x].push_back(y);
b[y].push_back(x);
else
a[x].push_back(y);
a[y].push_back(x);
b[x].push_back(y);
b[y].push_back(x);
}
spfa(1);
memset(vis,0,sizeof vis);
SPFA(n);
for(int i=1;i<=n;i++)
ans=max(ans,maxn[i]-minn[i]);
printf("%d\n",ans);
return 0;
}
洛谷上某暴力代码
#include<bits/stdc++.h>
#define INF 0x7f7f7f7f
#define MAXN 100005
using namespace std;
vector<int> g[MAXN];
int n,m,f[MAXN],mi[MAXN],c[MAXN];
void dfs(int x,int minx,int pre) {
int flag=1;
minx=min(c[x],minx);
if (mi[x]>minx) mi[x]=minx,flag=0;
int maxx=max(f[pre],c[x]-minx);
if (f[x]<maxx) f[x]=maxx,flag=0;
if (flag) return;
for (int i=0;i<g[x].size();i++) dfs(g[x][i],minx,x);
}
int main() {
scanf("%d%d",&n,&m);
for (int i=0;i<MAXN;i++) mi[i]=INF;
for (int i=1;i<=n;i++) scanf("%d",&c[i]);
for (int i=1;i<=m;i++) {
int t1,t2,t3;
scanf("%d%d%d",&t1,&t2,&t3);
g[t1].push_back(t2);
if (t3==2) g[t2].push_back(t1);
}
dfs(1,INF,0);
printf("%d\n",f[n]);
return 0;
}
装满的油箱
标签:dp

设dp[i][j]表示走到城市i,剩余油量为j的最小花费。因为加油操作和移动操作是相互独立的,那么,我们可以分别去计算这两个步骤,设当前所在城市为 v,所剩汽油为 j,得到下面看到的这样两个转移方程式:
dp[v][j+1]=min(dp[v][j+1], dp[v][j]+pc (j < c)
dp[u][j-d]=min(dp[u][j-d],dp[v][j]) (j>d 且 e(u,v,d)∈E)
因为我们需要的是最终的花费最小,因此,我们用一个优先队列存储所有能够到达的答案,每次从开销
最小的那个方案开始往外进行搜索,直到到达终点为止。
Code
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
#include <vector>
using namespace std;
#define maxn 1005
#define maxc 105
struct edge {
int v, w;
edge() {}
edge(int v, int w) : v(v), w(w) {}
};
struct node {
int v, fl, ct;
node() {}
node(int v, int fl, int ct) : v(v), fl(fl), ct(ct) {}
bool operator<(const node &b) const { return ct > b.ct; }
};
int N, M, Q, P[maxn], dis[maxn][maxc];
vector<edge> G[maxn];
void solve() {
int s, e, c;
scanf("%d%d%d", &c, &s, &e);
memset(dis, 0x3f, sizeof(dis));
dis[s][0] = 0;
priority_queue<node> q;
q.push(node(s, 0, 0));
while (!q.empty()) {
node t = q.top();
q.pop();
if (t.v == e) {
printf("%d\n", t.ct);
return;
}
if (t.fl < c) {
int d = t.ct + P[t.v];
if (d < dis[t.v][t.fl + 1])
dis[t.v][t.fl + 1] = d, q.push(node(t.v, t.fl + 1, d));
}
for (int i = 0; i < (int)G[t.v].size(); ++i) {
edge &e = G[t.v][i];
if (t.fl >= e.w) {
if (t.ct < dis[e.v][t.fl - e.w])
dis[e.v][t.fl - e.w] = t.ct, q.push(node(e.v, t.fl - e.w,t.ct));
}
}
}
puts("impossible");
}
int main() {
scanf("%d%d", &N, &M);
for (int i = 0; i < N; ++i) scanf("%d", P + i);
for (int i = 0; i < M; ++i) {
int u, v, d;
scanf("%d%d%d", &u, &v, &d);
G[u].push_back(edge(v, d));
G[v].push_back(edge(u, d));
}
scanf("%d", &Q);
while (Q--) solve();
return 0;
}
道路游戏
(注:因笔者太菜不会斜率优化,代码是卡过的。。。)
标签:dp

看到这个题面的时候我已经什么都不想说了。看懂后依稀觉得是个dp,用三维dp做了半天无果,心态也炸掉了……
对于这个题而言,需要考虑的有以下几个内容:
- 每时每刻都必须有一个机器人位于环上
- 机器人可以从任意位置开始制造
- 对于每个时刻 ,都会花一定的时间收集金币
因此,我们可以直接用一个(O3 )的暴力去解决这个问题
设dp[i] 为 i 时刻的最大收益,那么可以得到:
dp[i] = max{ dp[i - k] + sum - cost[j - k] }
k为枚举的这个机器人的使用时间 ,机器人从j - k号工厂出发,走 k 次在时刻 i 到达工厂j的最优解
Code
#include<bits/stdc++.h>
using namespace std;
int a[1005][1005],cost[1005],f[1005];
int main() {
int n,m,p;
scanf("%d %d %d",&n,&m,&p);
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
scanf("%d",&a[i][j]);
}
}
for(int i=1;i<=n;i++) scanf("%d",&cost[i]);
for(int i=1;i<=n;i++) f[i] = -0x3f3f3f3f;
f[0]=0;
for(int i=1;i<=m;i++) {
for(int j=1;j<=n;j++) {
int sum=0,t=j-1;
if(!t) t=n;
sum = a[t][i];
for(int k=1;k<=p;k++) {
if(i - k < 0) break;
f[i]=max(f[i],f[i - k] + sum - cost[t]);
t--;
if(!t) t=n;
sum += a[t][i - k];
}
}
}
printf("%d",f[m]);
return 0;
}
本文来自博客园,作者:Doria_tt,转载请注明原文链接:https://www.cnblogs.com/pangtuan666/p/16602030.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号