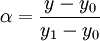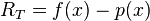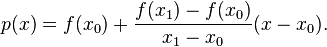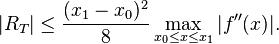维基百科 线性插值

如何进行线性插值

假设我们已知坐标 (x₀, y₀) 与 (x₁, y₁)，要得到 [x₀, x₁] 区间内某一位置 x 在直线上的值。根据图中所示，我们得到

假设方程两边的值为 α，那么这个值就是插值系数—从 x₀ 到 x 的距离与从x₀ 到 x₁ 距离的比值。由于 x 值已知，所以可以从公式得到 α 的值

同样，

这样，在代数上就可以表示成为：

或者，

这样通过 α 就可以直接得到 y。实际上，即使 x 不在 x₀ 到 x₁ 之间并且 α 也不是介于 0 到 1 之间，这个公式也是成立的。在这种情况下，这种方法叫作线性外插—参见 外插值。

已知 y 求 x 的过程与以上过程相同，只是 x 与 y 要进行交换。

线性插值近似法

线性插值经常用于已知函数 f 在两点的值要近似获得其它点数值的方法，这种近似方法的误差定义为

其中 p 表示上面定义的线性插值多项式

根据罗尔定理，我们可以证明：如果 f 有两个连续导数，那么误差范围是

正如所看到的，函数上两点之间的近似随着所近似的函数的二阶导数的增大而逐渐变差。从直观上来看也是这样：函数的曲率越大，简单线性插值近似的误差也越大。

应用

线性插值经常用于补充表格中的间隔部分。假设一个表格列出了一个国家 1970年、1980年、1990年以及 2000年的人口，那么如果需要估计 1994年的人口的话，线性插值就是一种简便的方法。

两值之间的线性插值基本运算在计算机图形学中的应用非常普遍，以至于在计算机图形学领域的行话中人们将它称为 lerp。所有当今计算机图形处理器的硬件中都集成了线性插值运算，并且经常用来组成更为复杂的运算：例如，可以通过三步线性插值完成一次双线性插值运算。由于这种运算成本较低，所以对于没有足够数量条目的光滑函数来说，它是实现精确快速查找表的一种非常好的方法。

历史

线性插值从远古以来就一直用于补充表格中的间隔，它经常用于天文学数据。人们相信公元前最后三个世纪的塞琉西王朝、公元前2世纪的希腊天文学家与数学家喜帕恰斯就曾经使用了这种方法。在托勒密于公元2世纪所作的《天文学大成》（Almagest）中亦可以见到对于线性插值的描述。

其它

在一些要求较高的场合，线性插值经常无法满足要求。在这种场合，可以使用多项式插值或者样条插值来代替。

线性插值可以扩展到有两个变量的函数的双线性插值。双线性插值经常作为一种粗略的抗混叠滤波器使用，三线性插值用于三个变量的函数的插值。线性插值的其它扩展形势可以用于三角形与四面体等其它类型的网格运算。