hdu4488 Faulhaber’s Triangle(模拟题)
Faulhaber’s Triangle
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 157 Accepted Submission(s): 78
Problem Description
The sum of the m
th powers of the first n integers
S(n,m) = SUM ( j= 1 to n)( j m)
Can be written as a polynomial of degree m+1 in n:
S(n,m) = SUM (k = 1 to m+1)(F(m,k) *n k)
Fo example:
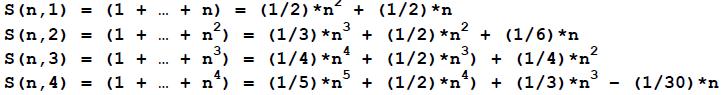
The coefficients F(m,k) of these formulas form Faulhaber‘s Tr angle:
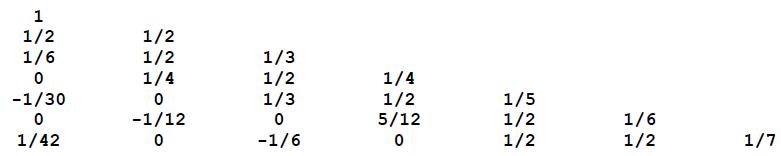
where rows m start with 0 (at the top) and columns k go from 1 to m+1
Each row of Faulhaber‘s Tr angle can be computed from the previous row by:
a) The element in row i and column j ( j>1) is (i/j )*(the element above left); that is:
F(i,j ) = (i/j )*F(i-1, j-1)
b) The first element in each row F(i,1) is chosen so the sum of the elements in the row is 1
Write a program to find entries in Faulhaber‘s Tr angle as decimal f actions in lowest terms
S(n,m) = SUM ( j= 1 to n)( j m)
Can be written as a polynomial of degree m+1 in n:
S(n,m) = SUM (k = 1 to m+1)(F(m,k) *n k)
Fo example:
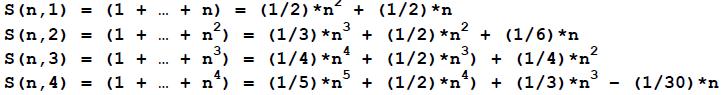
The coefficients F(m,k) of these formulas form Faulhaber‘s Tr angle:
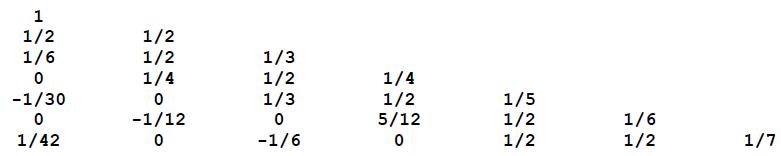
where rows m start with 0 (at the top) and columns k go from 1 to m+1
Each row of Faulhaber‘s Tr angle can be computed from the previous row by:
a) The element in row i and column j ( j>1) is (i/j )*(the element above left); that is:
F(i,j ) = (i/j )*F(i-1, j-1)
b) The first element in each row F(i,1) is chosen so the sum of the elements in the row is 1
Write a program to find entries in Faulhaber‘s Tr angle as decimal f actions in lowest terms
Input
The first line of input contains a single integer P, (1 <= P <= 1000), which is the number of data sets that follow. Each data set should be processed identically and independently
Each data set consists of a single line of input consisting of three space separated decimal integers The first integer is the data set number. The second integer is row number m, and the third integer is the index k within the row of the entry for which you are to find F(m, k), the Faulhaber‘s Triangle entry (0 <= m <= 400, 1 <= k <= n+1).
Each data set consists of a single line of input consisting of three space separated decimal integers The first integer is the data set number. The second integer is row number m, and the third integer is the index k within the row of the entry for which you are to find F(m, k), the Faulhaber‘s Triangle entry (0 <= m <= 400, 1 <= k <= n+1).
Output
For each data set there is a single line of output. It contains the data set number, followed by a single space which is then followed by either the value if it is an integer OR by the numerator of the entry, a forward slash and the denominator of the entry.
Sample Input
4
1 4 1
2 4 3
3 86 79
4 400 401
Sample Output
1 -1/30
2 1/3
3 -22388337
4 1/401
Source
第一项等于1减去后面的所有项,注意一下,用__int64存,不然会爆掉,我的156ms还不错呢
今天做了几题,好充实的感觉,哈哈
#include<stdio.h>
struct nod{
__int64 a,b;
}s[405][405];
__int64 gy(__int64 a,__int64 b)
{
__int64 temp;
if(b==0||a==0)
return 0;
if(a<0)
a=-a;
if(b<0)
b=-b;
if(a<b)
{
temp=a;
a=b;
b=temp;
}
while((temp=a%b))
{
a=b;
b=temp;
}
return b;
}
int Init()
{
int i,j,k,n;
__int64 t1,t2,temp;
s[0][1].a=1;
s[0][1].b=1;
s[1][1].a=1;
s[1][1].b=2;
s[1][2].a=1;
s[1][2].b=2;
for(i=2;i<401;i++)
{
for(j=2;j<=i+1;j++)
{
t1=i*s[i-1][j-1].a;
t2=j*s[i-1][j-1].b;
if((temp=gy(t2,t1)))
{
t1/=temp;
t2/=temp;
}
else
{
t1=0;
t2=1;
}
s[i][j].a=t1;
s[i][j].b=t2;
}
t1=0;
t2=1;
for(j=2;j<=i+1;j++)//2项开始求后面的和
{
t1=t2*s[i][j].a+t1*s[i][j].b;
t2=t2*s[i][j].b;
if((temp=gy(t1,t2)))
{
t1/=temp;
t2/=temp;
}
else
{
t1=0;
t2=1;
}
}
t1=t2-t1;
if((temp=gy(t1,t2)))
{
t1/=temp;
t2/=temp;
}
else
{
t1=0;
t2=1;
}
s[i][1].a=t1;
s[i][1].b=t2;
}
return 1;
}
int main()
{
int i,j,k,n,t,no,x,y;
Init();
scanf("%d",&t);
while(t--)
{
scanf("%d%d%d",&no,&x,&y);
printf("%d ",no);
if(s[x][y].a==0)
printf("0\n");
else if(s[x][y].b==1)
printf("%I64d\n",s[x][y].a);
else printf("%I64d/%I64d\n",s[x][y].a,s[x][y].b);
}
return 0;
}



