B Rinne Loves Xor 异或题

题意：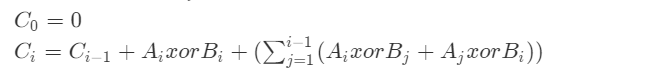

 

 思路：假如直接计算，那么复杂度会达到n^2

　　　 于是，我们需要一种复杂度较低的做法；　　　　

　　　 假如有这样一个二进制数 1 1 1

　　　 然后我们有另一个二进制数0 0 1

　　　 那么这两个数的异或计算方式为：1 1 1^0 0 1

　　     也可以为：（0 0 1）^ 0 0 1+0 1 0^ 0 0 1 + 1 0 0 ^0 0 1(即，把前面的数一位一位拆开分开计算)

　　     于是，我们可以想到另一种做法，就是把数按二进制位置存下来；

　　　  然后根据这一个位置的0 1 数量来计算和即可

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
const int N=1e5+5;
int a[N],b[N],A[40][2],B[40][2];
ll c[N];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)
        scanf("%d",&b[i]);
    c[0]=0;
    for(int i=1;i<=n;i++){
        c[i]=c[i-1]+(a[i]^b[i])%mod;
        for(int j=0;j<=30;j++){
            int t=(a[i]>>j)&1;
            c[i]=(c[i]+1LL*B[j][1-t]*(1<<j)%mod)%mod;
            t=(b[i]>>j)&1;
            c[i]=(c[i]+1LL*A[j][1-t]*(1<<j)%mod)%mod;
            A[j][(a[i]>>j)&1]++;
            B[j][(b[i]>>j)&1]++;
        }
    }
    for(int i=1;i<=n;i++)
        printf("%lld%c",c[i]%mod,i==n?'\n':' ');
    return 0;
}