差分数组
一、差分数组的定义及用途
1.定义:
对于已知有n个元素的离线数列d,我们可以建立记录它每项与前一项差值的差分数组f:显然,f[1]=d[1]-0=d[1];对于整数i∈[2,n],我们让f[i]=d[i]-d[i-1]。
2.简单性质:
(1)计算数列各项的值:观察d[2]=f[1]+f[2]=d[1]+d[2]-d[1]=d[2]可知,数列第i项的值是可以用差分数组的前i项的和计算的,即d[i]=f[i]的前缀和。
(2)计算数列每一项的前缀和:第i项的前缀和即为数列前i项的和,那么推导可知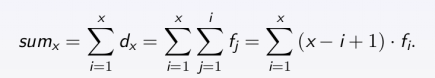
即可用差分数组求出数列前缀和;
3.用途:
(1)快速处理区间加减操作:
假如现在对数列中区间[L,R]上的数加上x,我们通过性质(1)知道,第一个受影响的差分数组中的元素为f[L],即令f[L]+=x,那么后面数列元素在计算过程中都会加上x;最后一个受影响的差分数组中的元素为f[R],所以令f[R+1]-=x,即可保证不会影响到R以后数列元素的计算。这样我们不必对区间内每一个数进行处理,只需处理两个差分后的数即可;
(2)询问区间和问题:
由性质(2)我们可以计算出数列各项的前缀和数组sum各项的值;那么显然,区间[L,R]的和即为ans=sum[R]-sum[L-1];
二、相关题目
1.[HDU1556]Color the ball
Description
-N个气球排成一排,从左到右依次编号为1,2,3....N.每次给定2个整数a b(a <= b),lele便为骑上他的“小飞鸽"牌电动车从气球a开始到气球b依次给每个气球涂一次颜色。但是N次以后lele已经忘记了第I个气球已经涂过几次颜色了,你能帮他算出每个气球被涂过几次颜色吗?
-Input:每个测试实例第一行为一个整数N,(N <= 100000).接下来的N行,每行包括2个整数a b(1 <= a <= b <= N)。当N = 0,输入结束。
-Output:每个测试实例输出一行,包括N个整数,第I个数代表第I个气球总共被涂色的次数。
Solution
1.记录各次操作,对差分数组进行对应修改,改变量为1(用途1);
2.使用性质(1)计算各项的值即可;
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<cstring> 5 #include<algorithm> 6 using namespace std; 7 int d[100010],a[100010],l,r; 8 int main(){ 9 int n; 10 while(scanf("%d",&n),n) 11 { 12 memset(d,0,sizeof(d)); 13 memset(a,0,sizeof(a)); 14 for(int i=1;i<=n;++i){ 15 scanf("%d%d",&l,&r); 16 d[l]+=1; 17 d[r+1]-=1; 18 } 19 for(int i=1;i<=n;++i) a[i]=a[i-1]+d[i]; 20 for(int i=1;i<n;++i) printf("%d ",a[i]); 21 printf("%d\n",a[n]); 22 } 23 return 0; 24 }
2.[NKOJ3754]数列游戏
Description
-给定一个长度为N的序列,首先进行A次操作,每次操作在Li和Ri这个区间加上一个数Ci。
然后有B次询问,每次询问Li到Ri的区间和。
初始序列都为0。
-输入格式:
第一行三个整数N A B。(1<=N<=1000000,1<=A<=N,A<=B<=N)
接下来A行,每行三个数Li Ri Ci。(1<=Li<=N,Li<=Ri<=N,|Ci|<=100000000000000)。
接下来B行,每行两个数 Li Ri。范围同上。
-输出格式:
对于每次询问,输出一行一个整数。
因为最后的结果可能很大,请对结果mod 1000000007。
Solution
1.应用(1)处理区间加;
2.用性质(1)求出修改后数列,再求出相应数列和(应用2)或直接用性质(2)求解;
3.注意随时取模;
1 #include<iostream> 2 #include<cmath> 3 #include<cstring> 4 #include<algorithm> 5 #include<cstdio> 6 const long long mod=1000000007; 7 using namespace std; 8 long long d[100010],f[100010],sum[100010]; 9 int main(){ 10 int n,a,b; 11 scanf("%d%d%d",&n,&a,&b); 12 memset(d,0,sizeof(d)); 13 memset(f,0,sizeof(f)); 14 memset(sum,0,sizeof(sum)); 15 for(int i=1;i<=a;++i){ 16 long long l,r,c; 17 scanf("%ld%ld%ld",&l,&r,&c); 18 f[l]=(f[l]+c)%mod; 19 f[r+1]=(f[r+1]-c)%mod; 20 } 21 for(int i=1;i<=n;++i) d[i]=(d[i-1]+f[i])%mod; 22 for(int i=1;i<=n;i++) sum[i]=(sum[i-1]+d[i])%mod; 23 for(int i=1;i<=b;++i){ 24 int l,r; 25 scanf("%d%d",&l,&r); 26 printf("%ld\n",(sum[r]-sum[l-1])%mod); 27 //printf("%ld\n",temp>=0?temp:temp+mod);//防止结果为负; 28 } 29 return 0; 30 }



