二叉搜索树

二叉搜索树的定义：

二叉搜索树或者是一棵空树，或者是具有下列性质的二叉树：

（1）若左子树不空，则左子树上所有结点的值均小于或等于它的根节点的值；

（2）若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；

（3）左、右子树也分别为二叉搜索树；

 

如图（一颗长残了的BST）：

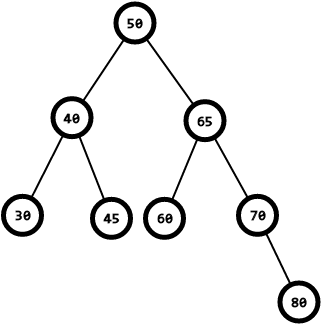
二叉搜索树的查询：

若根结点的关键字值等于查找的关键字，返回根节点的值。

否则，若小于根结点的关键字值，递归查左子树。 

若大于根结点的关键字值，递归查右子树。

若子树为空，则查找不成功。

 

假如我们要查询60

从根节点50开始，50 < 60 往右子树里找，到65，65 > 60 往右子树里找，找到60

 

二叉搜索树的插入：

与查询类似，判断在左子树还是右子树，走到叶节点后直接新加一个节点

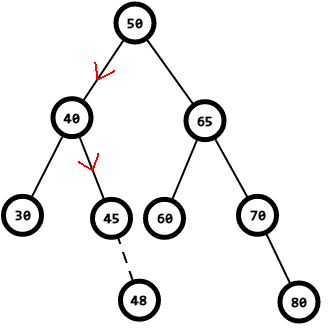
如图我们要插入48

48 < 50，去左子树，到40

48 > 40，去右子树，到45

48 > 45，45没有子节点了，48成为45的右儿子

二叉搜索树的最值：

最小值：一直往左子树里找

最大值：一直往右子树里找

二叉搜索树的前驱/后继：

前驱是第一个比这个数小的值，后继是第一个比这个大的值

性质：

　　节点x的前驱一定没有右儿子，可能有左儿子（若前驱y有右儿子z，z大于y小于x，那z就是x前驱）

　　节点x的后继一定没有左儿子，可能有右儿子（若前驱y有左儿子z，z小于y大于x，那z就是x前驱）

前驱：如果这个节点x有左子树，就以左儿子为根，查询左子树的最大值

　　   如果没有左子树（1）：如果x为右儿子，前驱就是x的父亲

　　　　　　　　　   （2）：如果x为左儿子，前驱就是右父亲的左父亲（若没有左父亲，就一直往上找）

如图：

50的前驱是45。（前驱是左子树最大值）

45的前驱是40。（没有左子树且为右儿子，前驱是其父亲）

60的前驱是50。（没有左子树且为左儿子，前驱是其右父亲的左父亲）

30没有前驱。    【没有左子树且为左儿子，但在30的左父亲（祖先）里没有有左父亲的节点】

---

 

后继：如果这个节点有右子树，就以右儿子为根，查询右子树的最大值

　　  如果没有右子树（1）：如果x为左儿子，后继就是x的父亲

　　　　　　　　　  （2）：如果x为右儿子，前驱就是左父亲的右父亲（若没有右父亲，就一直往上找）

同理如图：

50的后继是60。（前驱是右子树里最小的）

60的后继是65。（没有右子树且为左儿子，前驱是其父亲）

45的后继是50。（没有右子树且为右儿子，前驱是其左父亲的右父亲）

80无后继。　　 【没有右子树且为右儿子，但在80的左父亲（祖先）里没有有右父亲的节点】

 

二叉搜索树的删除：

 删除有三种情况：

情况1：删除点为叶节点

　　  直接删除

 

对于30，45，60，80这四个节点，即使删掉也不会改变原树的平衡，故直接删掉

情况2：删除点右一个儿子

　　  直接用儿子替换删除点的位置

如70，因为以70为根的子树均大于65，所以删掉70后直接把70的儿子80接到70的位置并不会影响原树的平衡

如果删除点只有左儿子同理，所以删除点只有一个儿子的话可以直接用儿子替换删除点

情况3：删除点右两个儿子

　　  找到删除点的后继，用后继代替删除点，然后让后继的儿子替换后继的位置（情况2）

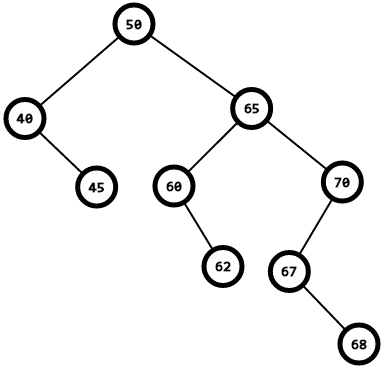
假设我们要删除65，那我们先找到65的后继67，把67放到65的位置上（因为65的右子树都大于65，所以67大于65的左子树，又因为67在65的右右子树里最小，所以67小于处67外的65的右子树，满足平衡条件），变成了这样

 

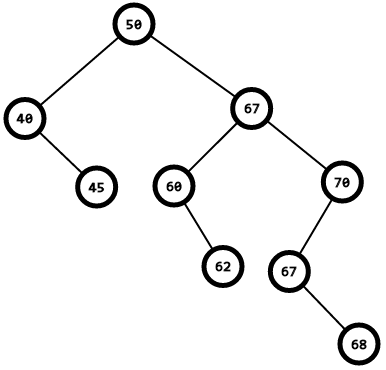
根据后继的性质，67没有左子树，只有一个右子树（一个儿子），因为67到了65的位置，所以67的位置空了出来（被删了），在加上67只有一个儿子，这不就是情况2吗，然后对67进行情况2的删除就可以了