数据结构与算法 --- 排序算法（一）

引言

按照时间复杂度，将一些常见排序算法进行分类，分为以下三类：

• \(O(n^2)\)：冒泡排序，插入排序，选择排序。

• \(O(nlogn)\)：快速排序，归并排序。

• \(O(n)\)：桶排序，计数排序，基数排序。

本篇文章讨论以下第一类：冒泡排序，插入排序，选择排序。

上一篇数据结构与算法 --- 如何分析排序算法提到，从三个方面分析排序算法：

• 排序算法的执行效率 - 时间复杂度

• 排序算法的内存消耗 - 原地排序算法/非原地排序算法

• 排序算法的稳定性 - 稳定排序算法/不稳定排序算法

那么，下面讨论一下这三种排序算法。

冒泡算法

冒泡排序（bubble sort）过程包含多次冒泡操作，每一次冒泡操作都会遍历整个数组，依次比较相邻元素，不符合大小关系则互换位置，直到无元素需要交换。

算法图解

那来看一下排序过程，假设有一组数据：1、6、9、3、7、2，按照从小到大的排序顺序排序，则第一轮的冒泡操作如下图：

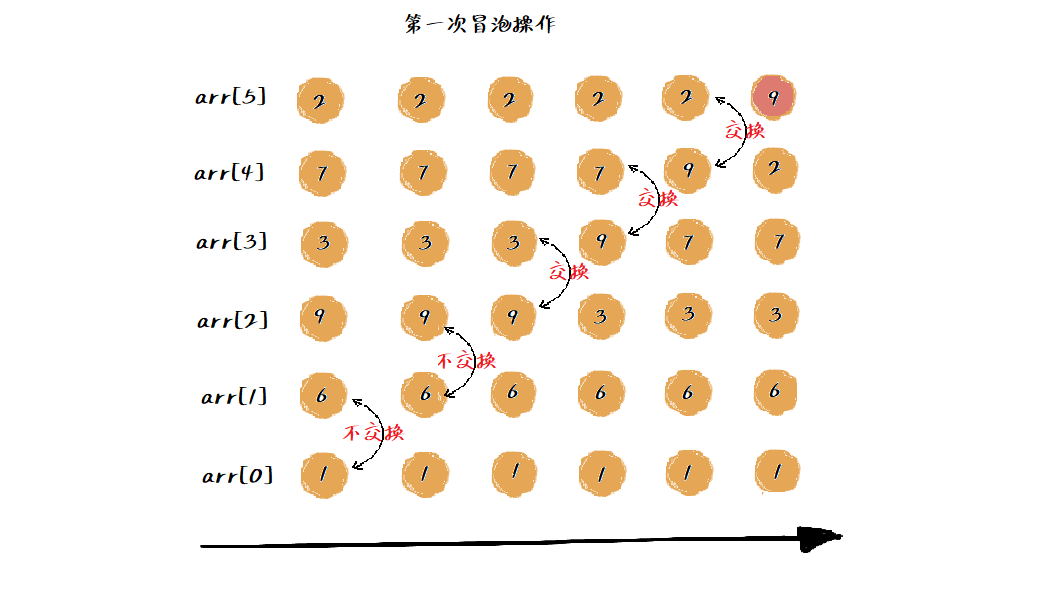
这样，最大的数已经排在最后一个了，在完成其他五个数的排序，在进行五次这样的冒泡操作就排序完成，如下图：

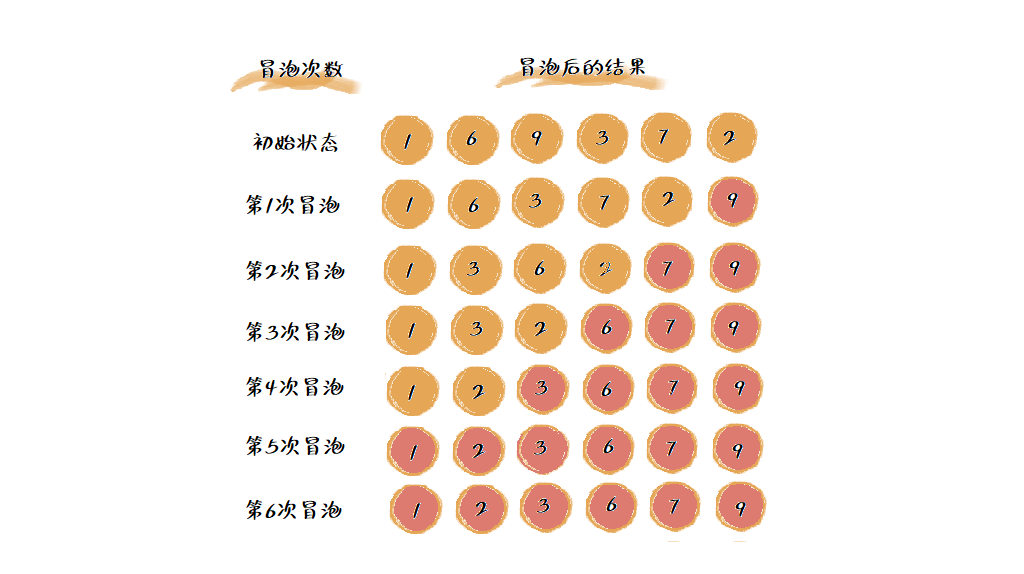
但是从上图也可以看出，在第四次冒泡的时候就已经排序完成，其实可以进行优化。当某一次冒泡操作已经没有数据交换时，说明已经排序完成，可以结束排序。

那么，使用C#实现一个冒泡排序如下：

public void BubbleSort(int[] arr)
{
    if (arr == null || arr.Length == 0)
        return;

    var length = arr.Length;
    //提前结束排序的标志
    bool flag = false;

    for (int i = 0; i < length; i++)
    {
        for (int j = 0; j < length - i - 1; j++)
        {
            if (arr[j] > arr[j + 1])
            {
                //交换元素
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;

                flag = true;
            }
        }
        //如果没有数据交换，则提前退出
        if (!flag)
            break;
    }
}

算法分析

1. 稳定性

   冒泡排序只涉及到相邻数据交换，只需要常量级的临时空间，空间复杂度为\(O(1)\)，是一个原地排序算法。

2. 内存消耗

   冒泡排序中，只有交换才可以改变两个元素的前后顺序，为了保证冒泡排序的稳定性，在冒泡过程中，我们对两个大小相等的相邻的元素不做交换，这就保证了相同大小的元素顺序在排序后不会改变。因此冒泡排序是一个稳定排序算法。

3. 时间复杂度

   最好的情况下，要排序的数据已经是有序的了，我们只需要进行一次冒泡操作，所以最好时间复杂度为\(O(1)\)。

   最坏的情况下，要排序的数据是倒序排列的，则需要 \(n\) 次冒泡操作，因此最坏时间复杂度为\(O(n^2)\)。

   对于平均时间复杂度，假设有 \(n\) 个数据的集合，有 \(n!\) 种不同的排列方式，所以很难直接计算时间复杂度。

所以计算排序算法的时间复杂度，需要另外一种思路：通过“有序度”和“无序度”这两个概念来进行分析：

• 有序度

  有序度是指数组中具有有序关系的元素对的个数，如果用数学式表达出来，就是：

  \[a[i] \leq a[j], \quad i<j \]

• 逆序度

  逆序度则跟有序度定义相反，是指数组中逆序元素对的个数（假设从小到大为有序） ，如果用数学式表达出来，就是：

  \[a[i] > a[j], \quad i<j \]

有序度和你序度使用图片表示出来如下图：

还有一个概念，当数组是一个倒叙（假设从小到大的为有序）的排列的数组时，有序度为0，逆序度为\(\frac{n(n-1)}{2}\)（该公式为排列组合公式），也就是15，当它时一个完全有序的数组时，有序度为\(\frac{n(n-1)}{2}\)，逆序度为0，像这种完全有序的数据的有序度称之为满有序度（\(\frac{n(n-1)}{2}\)）。

从上述定义中，也可以看出，数组的有序度，逆序度，满有序度存在一定关系：逆序度 = 满有序度 - 有序度>。排序的过程就是增加有序度，减少逆序度的过程。当最终有序度达到满有序度时，说明已经排序完成。

所以补充上述排序过程中有序度变化如下图：

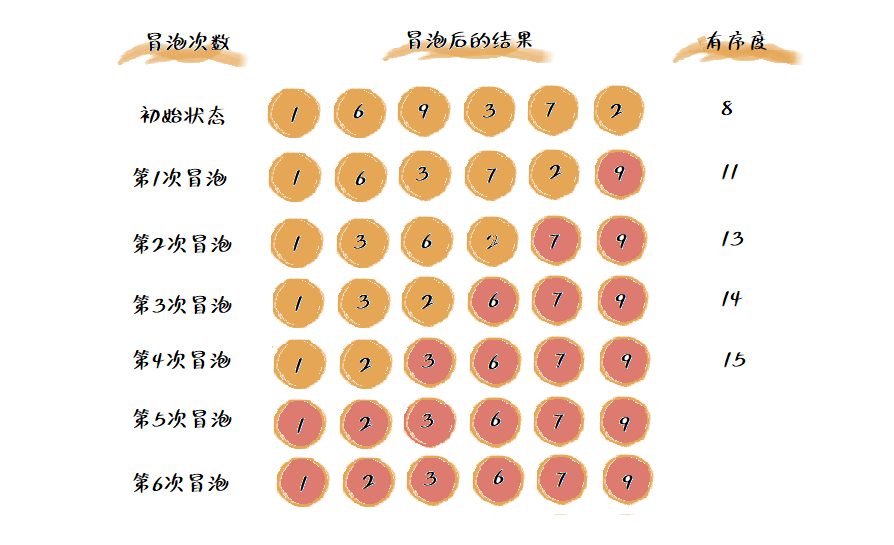
可以看到冒泡排序只有比较和交换两个操作，因为交换只会交换相邻两个元素，所以每一次交换，有序度就增加1。无论冒泡算法如何改进，它的总交换数是固定的，这个数也是逆序度，所以上图排序过程中的满排序度是15（\(\frac{6(6-1)}{2}\)），初始有序度为8，所以上述排序过程共进行了7次交换操作。

那么，有了有序度和逆序度两个概念后，对于包含\(n\)个数据的数组进行冒泡排序，平均交换次数是多少呢？

最坏情况下，初始有序度为0，因此要进行 \(\frac{n(n-1)}{2}\) 次交换。

最好情况下，初始有序度为 \(\frac{n(n-1)}{2}\) ，不需要交换。

我们可以取中间值 \(\frac{n(n-1)}{4}\) ，意味着要进行交换操作的量级是 \(n^2\) 。而比较操作肯定要比交换操作多，复杂度的上限是 \(O(n^2)\) （最坏时间复杂度），因此比较操作的量级也是 \(n^2\) ，综合比较和交换两部分操作，冒泡排序的平均情况下的时间复杂度为 \(O(n^2)\)。

:::warning{title="注意"}
该方式推导平均时间复杂度其实并不严格，但是概率论的定量分析太复杂，这样的方式在一定程度上是实用的。
:::

插入排序

先思考一下，对于一个有序数组（假设数组从小到大），往里边添加一个数后，如何让数组仍然保持有序？

答案其实简单，遍历数组，直到找到比它大的，站在它前边就好了，往后的都退一步都往后稍一稍就行，哈哈。
像这样：

这样的方案其实就是维护一个动态数组有序的方法，即动态的往有序集合中添加数据。

对于一个静态数据，也可以使用这种插队的方式来进行排序，于是就有了插入排序算法（insertion sort）。

那么如何实现插入排序：首先，可以将数组中的元素分为两个区间，已排序区间和未排序区间，初始已排序区间只有一个元素，就是数组的第一个元素，插入排序的核心思想是取未排序区间的元素，在已排序区间中找合适的位置插入，并保证已排序区间一直有序，重复该过程，直到未排序区间中元素未空。

算法图解

如下图：

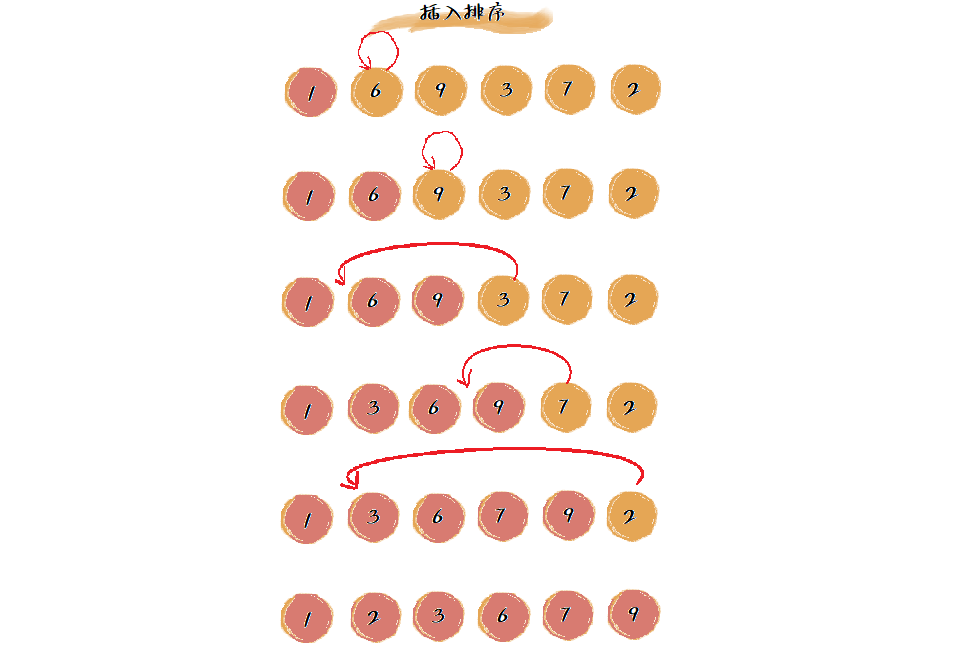
插入排序过程包含两种基本操作：元素的比较和移动。当我们需要将一个数据 a 插入到已排序区间时，需要用数据 a 与已排序区间的数据依次比较大小，找到合适的插入点。在找到插入点之后，我们还需要将插入点之后的数据顺序往后移动一位，这样才能腾出位置给数据 a 插入。对于不同的查找插入点方法(从头到尾、从尾到头)，总的比较次数是有区别的。但对于一个给定的初始序列，移动操作的总次数是固定的，就等于数组的逆序度。

为什么说移动次数就等于逆序度呢？

如下图所示，满有序度为 \(\frac{n(n-1)}{2}=15\)，初始有序度为8，逆序度为7，在下图中移动元素的个数之和也等于7（\(2+1+4=7\)）

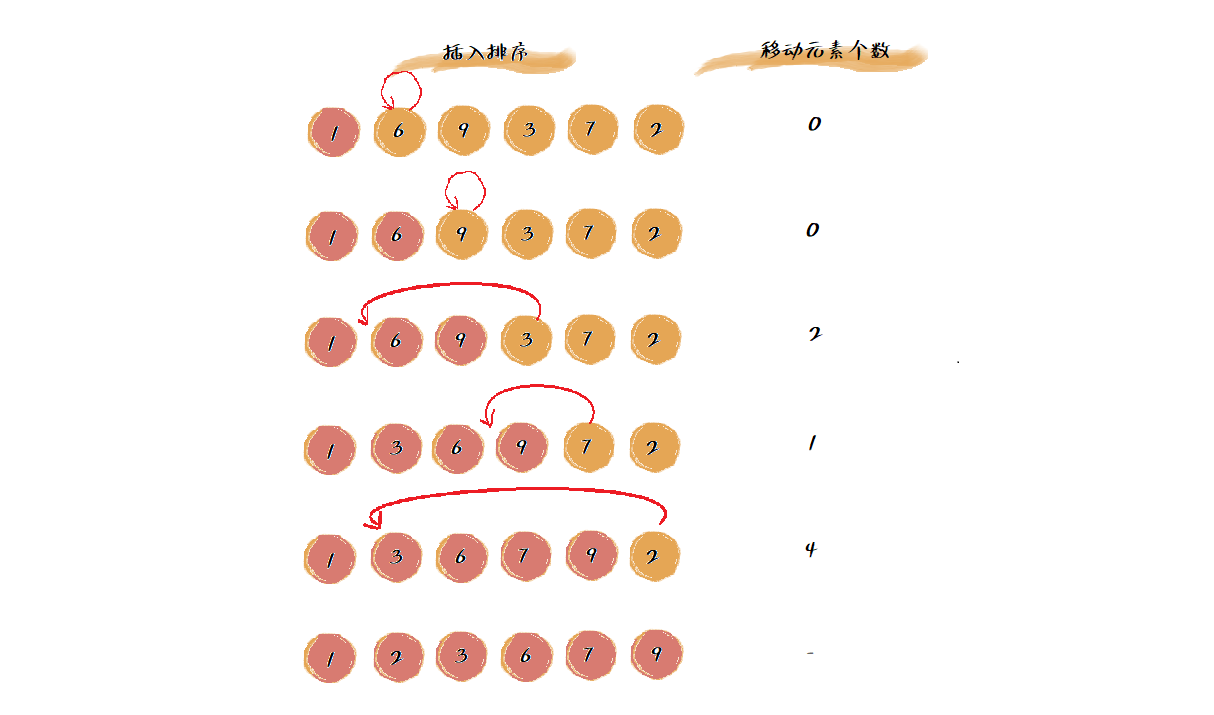
与冒泡排序算法一样，我们再来回答下面 3 个问题。
通过原理介绍和代码实现，我们可以很明显地看出，插入排序的运行过程并不需要额外的存储空间，因此，它是原地排序算法。同时，它的空间复杂度也是 \(O(1)\)。

那么，使用C#实现一个插入排序如下：

public static void InsertionSort(int[] arr)
{
    if (arr == null || arr.Length == 0) return;

    var length = arr.Length;

    //从第二个元素开始比较（未排序区间）
    for (int i = 1; i < length; i++)
    {
        var val = arr[i];

        //遍历已排序区间
        for (int j = i - 1; j >= 0; j--)
        {
            //按从小到大排序，所以如果目标元素比已排序元素小，则已排序区间往后移动一位
            if (arr[j] > val)
            {
                arr[j + 1] = arr[j];
            }
            else
            {
                arr[j + 1] = val;
                break;
            }
        }
    }
}

算法分析

接下来分析一下插入排序算法：

第一，插入排序是原地排序算法吗？

插入排序的过程只有移动元素，并不会创建额外存储空间，因此，它是原地排序算法，且空间复杂度为\(O(1)\)。

第二，插入排序是稳定排序算法吗？

对于未排序区间的某个元素，如果在已排序区间存在与它值相同的元素，我们选择将它插入到已排序区间值相同元素的后面，这样就可以保持值相同元素原有的前后顺序不变，因此插入排序是稳定排序算法。

第三，插入排序的时间复杂度是多少？

如果要排序的数据已经是有序的，我们就不需要移动任何数据。如果我们选择从尾到头在已排序区间里查找插入位置，那么每次只需要比较一个数据就能确定插入位置。因此，综合元素移动和比较的次数，最好时间复杂度为 \(O(n)\)。

如果数组是倒序的，那么每次插入都相当于在数组的第一个位置插入新的数据。因此，需要移动大量的数据，最坏时间复杂度为 \(O(n^2)\)。

还记得我们在数组中插入一个数据的平均时间复杂度是多少吗?

没错，是 \(O(n)\) 。因此对于插入排序，每次插入操作都相当于在数组中插入一个数据，循环执行 \(n\) 次插入操作，因此，平均时间复杂度为 \(O(n^2)\)。

选择排序

选择排序 (selection sort) 的实现思路类似插入排序，也将整个数组划分为已排序区间和未排序区间。两者的不同点在于: 选择排序每次从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

算法图解

选择排序图解如下：

使用C#实现一个选择排序如下：

public static void SelectionSort(int[] arr)
{
    if (arr == null || arr.Length == 0) return;

    var length = arr.Length;
    //只需循环length - 1次
    for (int i = 0; i < length - 1; i++)
    {
        int minPos = i;
        //找出最小值的索引
        for (int j = i; j < length; j++)
        {
            if (arr[j] < arr[minPos])
            {
                minPos = j;
            }
        }
        //交换元素
        int temp = arr[i];
        arr[i] = arr[minPos];
        arr[minPos] = temp;
    }
}    

算法分析

这里不再做详细分析，首先，它排序过程中没有产生额外存储空间，空间复杂度为 \(O(1)\)，是一种原地排序算法。

选择排序的最好时间复杂度、最坏时间复杂度、平均时间复杂度都为 \(O(n^2)\)。

那么选择排序是稳定排序算法吗？

选择排序是不稳定排序算法。从图解中可以看出，选择排序每次要找剩余未排序元素中的最小值，然后与前面的元素交换位置。这里的交换操作破坏了排序算法的稳定性。例如5、8、5、2、9这样一组数据，使用选择排序来排序的话，第一次找到最小的元素是 2，与第一个元素 5 交换位置，那么第一个 5 和中间的 5 的原有的先后顺序就改变了，因此，选择排序就是不稳定的了。

参考资料

[1] 数据结构与算法之美 / 王争 著. --北京：人民邮电出版社，2021.6