数据结构与算法 --- 算法绪论

开场白

算法介绍从一个简单加法开始，现要求写一个求1+2+3+..+100的结果的程序，那我可以这样写：

int count = 100;

int sum = 0;

for (int i =1; i <= count; i++)
{
    sum += i;
}

这就是最简单的程序之一，这就是算法。但是它是最优的吗？是最高效的吗？

儿时数学家高斯提出了另一种解法，他将两组1+2+3+..+100一组升序，一组降序进行组合，变成(1+100)+(2+99)+...(100+1)，像这样：

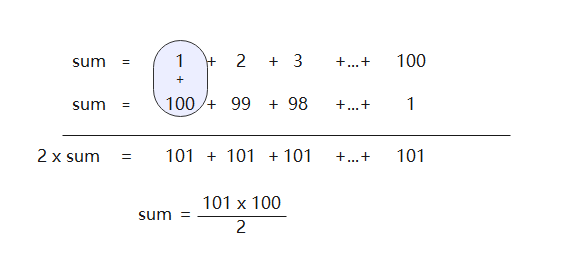
最后得到的公式就是后世的等差数列求和公式（首项 + 末项）x 项数 / 2）：
\(S_n = \frac{(a_1 +a_n )n}{2}\)

这样用程序来实现就是这样：

int count = 100;

int sum = 0;

sum = (1 + count) * count / 2;

这样的话，程序由运行一百次，就变成了运行一次，这就是更高效的算法。

算法的定义

什么是算法呢？算法就是描述解决问题的方法。

算法是解决特定问题求解步骤的描述，在计算机中表表现为指令的有限序列，并且每条指令表示一个或多个操作。

算法的特性

算法具有五个基本特性：输入、输出、有穷性、确定性和可行性。

• 输入输出

  输入和输出特性比较容易理解，算法具有零个或多个输入。尽管对于绝大多数算法来说，输入参数都是必要的，但对于个别情况，不需要任何输入参数，因此算法的输入可以是零个。算法至少有一个或多个输出，输出的形式可以是打印输出，也可以是返回一个或多个值等。

• 有穷性

  有穷性：指算法在执行有限的步骤之后，自动结束而不会出现无限循环，并且每一个步骤在可接受的时间内完成。现实中经常会写出死循环的代码，这就是不满足有穷性。

• 确定性

  确定性：算法的每一步骤都具有确定的含义，不会出现二义性。算法在一定条件下，只有一条执行路径，相同的输入只能有唯一的输出结果。算法的每个步骤被精确定义而无歧义。

• 可行性

  可行性：算法的每一步都必须是可行的，也就是说，每一步都能够通过执行有限次数完成。

算法设计的要求

一个合格的算法要基本符合这些要求，例如正确性，可读性，健壮性，时间效率高和存储量低。

正确性

正确性：算法的正确性是指算法至少应该具有输入、输出和加工处理无歧义性、能正确反映问题的需求、能够得到问题的正确答案。但是算法的“正确”通常在用法上有很大的差别，大体分为以下四个层次。

1. 算法程序没有语法错误。
2. 算法程序对于合法的输入数据能够产生满足要求的输出结果。
3. 算法程序对于非法的输入数据能够得出满足规格说明的结果。
4. 算法程序对于精心选择的，甚至***难的测试数据都有满足要求的输出结果。

对于这四层含义，层次1要求最低，但是仅仅没有语法错误实在谈不上是好算法。这就如同仅仅解决温饱，不能算是生活幸福一样。而层次4是最困难的，我们几乎不可能逐一验证所有的输入都得到正确的结果。因此算法的正确性在大部分情况下都不可能用程序来证明，而是用数学方法证明的。证明一个复杂算法在所有层次上都是正确的，代价非常昂贵。所以一般情况下，我们把层次3作为一个算法是否正确的标准。

可读性

可读性：算法设计的另一目的是为了便于阅读、理解和交流。
可读性高有助于人们理解算法，晦涩难懂的算法往往隐含错误，不易被发现，并且难于调试和修改。

我们写代码的目的，一方面是为了让计算机执行，但还有一个重要的目的是为了便于他人阅读，让人理解和交流，自己将来也可能阅读，如果可读性不好，时间长了自己都不知道写了些什么。可读性是算法（也包括实现它的代码）好坏很重要的标志。

健壮性

一个好的算法还应该能对输入数据不合法的情况做合适的处理。比如输入的时间或者距离不应该是负数等。

健壮性：当输入数据不合法时，算法也能做出相关处理，而不是产生异常或莫名其妙的结果。

时间效率高和存储量低

时间效率指的是算法的执行时间，对于同一个问题，如果有多个算法能够解决，执行时间短的算法效率高，执行时间长的效率低。

存储量需求指的是算法在执行过程中需要的最大存储空间，主要指算法程序运行时所占用的内存或外部硬盘存储空间。设计算法应该尽量满足时间效率高和存储量低的需求。

算法效率的度量方法

事后统计方法

这种方法主要是通过设计好的测试程序和数据，利用计算机计时器对不同算法编制的程序的运行时间进行比较，从而确定算法效率的高低。

但是有缺陷：

• 必须依据算法事先编制好程序，这通常需要花费大量的时间和精力。如果编制出来发现它根本是很糟糕的算法，不是竹篮打水一场空吗？

• 时间的比较依赖计算机硬件和软件等环境因素，有时会掩盖算法本身的优劣。

• 算法的测试数据设计困难，并且程序的运行时间往往还与测试数据的规模有很大关系，效率高的算法在小的测试数据面前往往得不到体现。

事前分析估算方法

在计算机程序编制前，依据统计方法对算法进行估算。

经过分析，一个用高级程序语言编写的程序在计算机上运行时所消耗的时间取决于下列因素：

• 算法采用的策略、方法。

• 编译产生的代码质量。

• 问题的输入规模。

• 机器执行指令的速度。

第1条当然是算法好坏的根本，第2条要由软件来支持，第4条要看硬件性能。也就是说，抛开这些与计算机硬件、软件有关的因素，一个程序的运行时间，依赖于算法的好坏和问题的输入规模。所谓问题输入规模是指输入量的多少。

函数的渐进增长

函数的渐近增长是指当自变量趋近于正无穷时，函数增长的趋势。通俗来说，可以想象一条直线在平面上向右无限延伸，而函数就是这条直线上的一个点，当自变量趋近于正无穷时，函数的值会随着自变量的增加而增加。而函数的渐近增长就是描述这个增长的速度和趋势。

举个例子，如果一个函数的渐近增长是线性的，那么当自变量增加一单位时，函数的值也会增加一单位，这种增长趋势可以用直线来描述。而如果一个函数的渐近增长是指数级的，那么当自变量增加一单位时，函数的值会增加很多单位，这种增长趋势可以用指数函数来描述。

在算法分析和计算机科学中，函数的渐近增长非常重要，因为它可以帮助我们预估算法的时间复杂度和空间复杂度，从而优化算法的效率。通过对函数的渐近增长的分析，我们可以找到最优的算法实现方式，以达到最快的运行速度和最少的资源消耗。

算法的时间复杂度

定义

在进行算法分析时，语句总的执行次数\(T(n)\)是关于问题规模\(n\)的函数，进而分析\(T(n)\)随\(n\)的变化情况并确定\(T(n)\)的数量级。

算法的时间复杂度，也就是算法的时间量度，记作：\(T(n)=O(f(n))\)。它表示随问题规模n的增大，算法执行时间的增长率和\(f(n)\)的增长率相同，称作算法的渐近时间复杂度，简称为时间复杂度。其中\(f(n)\)是问题规模\(n\)的某个函数。

这样用大写\(O()\)来体现算法时间复杂度的记法，称之为大O算法。

一般情况下，随着\(n\)的增大，\(T(n)\)增长最慢的算法为最优算法。

算法的渐进复杂度

在计算机科学中，大O表示算法的渐进复杂度。它是用来描述算法的时间或空间复杂度的一种方式。当我们说一个算法的复杂度为\(O(f(n))\)时，我们指的是当输入大小为\(n\)时，算法的运行时间或空间复杂度与\(f(n)\)成正比。通常，我们会使用最高阶的项来表示算法的复杂度，因为它在输入趋近于无穷大时最能反映算法的增长率。

推导算法的时间复杂度通常可以通过以下步骤来实现：

1. 确定算法的基本操作：算法中最基本的操作是什么？例如，基本操作可以是赋值、比较、加减乘除等。

2. 分析算法的代码：对算法代码进行分析，找到每个基本操作所对应的执行次数。

3. 计算时间复杂度：将每个基本操作的执行次数乘以其所需的时间复杂度，再将所有操作的时间复杂度相加，得到总的时间复杂度。

4. 推导大O阶：将得到的总的时间复杂度，经过系列步骤推导，最终得到的就是大O阶。

推导大O阶方法：

• 用常数1取代运行时间中的所有加法常数。

• 在修改后的运行次数函数中，只保留最高阶项。

• 如果最高阶项存在且不是1，则去除与这个项相乘的常数。得到的结果就是大O阶。

推导大O阶的过程涉及到分析算法的每个步骤的时间复杂度，并计算这些步骤的总时间复杂度。最终，我们将得到一个表示算法复杂度的数学表达式。例如，如果我们正在分析一个简单的循环，其中每次迭代的时间复杂度为\(O(1)\)，并且循环执行\(n\)次，则总时间复杂度为\(O(n)\)。如果我们分析的是一个递归算法，那么我们需要使用递归方程来推导出算法的复杂度。

推导大O阶需要对算法的实现细节有深入的理解，以便能够准确地计算每个步骤的时间复杂度，并最终得出算法的总时间复杂度。

常见的时间复杂度

常见的时间复杂度如下所示：

执行次数函数	阶	非正式术语
\(10\)	\(O(1)\)	常数阶
\(2n+3\)	\(O(n)\)	线性阶
\(3n^2+2n+1\)	\(O(n^2)\)	平方阶
\(5log_2n+20\)	\(O(logn)\)	对数阶
\(2n+4log_2n+12\)	\(O(nlogn)\)	nlogn阶
\(3n^3+2n^2+5n+13\)	\(O(n^3)\)	立方阶
\(2^n\)	\(O(2^n)\)	指数阶

常用的时间复杂度所消耗的时间从小到大排序为

\(O(1)\) < \(O(logn)\) < \(O(n)\) < \(O(nlogn)\) < \(O(n^2)\) < \(O(n^3)\) < \(O(2^n)\) < \(O(n!)\) < \(O(n^n)\)

最坏情况与平均情况

我们查找一个有个随机数字数组中的某个数字，最好的情况是第一个数字就是，那么算法的时间复杂度为\(O(1)\)，但也有可能这个数字就在最后一个位置上待着，那么算法的时间复杂度就是\(O(n)\)，这是最坏的一种情况了。

最坏情况运行时间是一种保证，那就是运行时间将不会再坏了。在应用中，这是一种最重要的需求，通常，除非特别指定，我们提到的运行时间都是最坏情况的运行时间。

而平均运行时间也就是从概率的角度看，这个数字在每一个位置的可能性是相同的，所以平均的查找时间为\(n/2\)次后发现这个目标元素。

平均运行时间是所有情况中最有意义的，因为它是期望的运行时间。也就是说，我们运行一段程序代码时，是希望看到平均运行时间的。可现实中，平均运行时间很难通过分析得到，一般都是通过运行一定数量的实验数据后估算出来的。

对算法的分析，一种方法是计算所有情况的平均值，这种时间复杂度的计算方法称为平均时间复杂度。另一种方法是计算最坏情况下的时间复杂度，这种方法称为最坏时间复杂度。一般在没有特殊说明的情况下，都是指最坏时间复杂度。

空间复杂度

算法的空间复杂度是指在算法执行过程中所需要的内存空间大小，通常用空间复杂度来衡量算法所占用的内存资源大小。算法空间复杂度的计算公式记作：\(S(n)=O(f(n))\)，其中，\(n\)为问题的规模，\(f(n)\)为语句关于\(n\)所占存储空间的函数。

结尾语

错误思想：

认为现在CPU速度越来越快，内存越来越大，算法的细微的优劣是用户体验不到的。

数据验证：

假设CPU在短短几年间，速度提高了100倍，这其实已经很夸张了。而我们的某个算法本可以写出时间复杂度是\(O(n)\)的程序，却写出了\(O(n^2)\)的程序，仅仅因为容易想到，也容易写。即在\(O(n^2)\)的时间复杂度算法程序下，速度其实只提高了10倍（\(\sqrt[2]{100}\)=10），而对于\(O(n)\)时间复杂度的算法来说，那才是真的100倍。

结论：

也就是说，一台老式CPU的计算机运行\(O(n)\)的程序和一台速度提高100倍新式CPU运行\(O(n^2)\)的程序。最终效率高的胜利方却是老式CPU的计算机，原因就在于算法的优劣直接决定了程序运行的效率。

参考资料

[1] 大话数据结构 / 程杰 著. --北京：清华大学出版社，2011.6