结对项目作业

项目	内容
这个作业属于那个课程	班级博客
这个作业的要求在哪里	作业要求
我在这个课程的目标是	学习软件工程相关知识，锻炼软件开发能力。
这个作业在哪个具体方面帮我实现目标	完成团队项目，体会结对编程。
作业正文	作业正文

1.About（1'）

教学班级：005
项目地址：https://github.com/Pandapan-Buaa/IntersectInPair

2.PSP表格

在开始实现程序之前，在下述 PSP 表格记录下你估计将在程序的各个模块的开发上耗费的时间。（0.5' + 0.5'）

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
·Estimate	估计这个任务需要多少时间	30	30（阅读具体要求，完成了博客框架）
Development	开发
·Analysis	需求分析 (包括学习新技术)	600	480（相关算法，QT/QcustomPlot学习）
·Design Spec	生成设计文档	30	30
·Design Review	设计复审 (和同事审核设计文档)	10	10
·Coding Standard	代码规范 (为目前的开发制定合适的规范)	10	10
·Design	具体设计	60	30（实际上沿用了上次的设计思路，增加附加圆部分，ui部分的设计则是摸索官方文档前进的，未算入此中）
·Coding	具体编码	480	240（QT+QcustomPlot比预想简单很多）
·Code Review	代码复审	60	60
·Test	测试（自我测试，修改代码，提交修改）	60	90
Reporting	报告
·Test Report	测试报告	30	30
·Size Measurement	计算工作量	30	20
·Postmortem & Process Improvement Plan	事后总结, 并提出过程改进计划	120	240（将写文档的部分包含于此处）
	合计	1520	1270

本次沿用了我在上次单人作业的参考架构（即《算法竞赛入门经典：训练指南》4.1.2 和 4.2.1小节》中关于计算几何的内容），因此在简单修改后便得到了扩展计算交点功能的代码。由于两人远程合作的不便，剩余的任务则是直接一分为二，我来负责UI部分，另一位同学负责测试以及错误处理的部分。这部分表格记录的是UI以及核心代码计算部分的时间，相对预估减少了不少，因为在看完QT和QcustomPlot的相关资料后，发现实现起来并不复杂。

3.Information Hiding，Interface Design，Loose Coupling

看教科书和其它资料中关于 Information Hiding，Interface Design，Loose Coupling 的章节，说明你们在结对编程中是如何利用这些方法对接口进行设计的。（5'）

事实上核心代码行数在300行以内，每个类也并无私有属性，设计时只要按基本的信息隐藏和接口设计原则就可以。
具体如第五部分UML类图所示，由于每个类中的属性与方法都是需要提供给外部交点计算函数的，因此均为public（当然可以把交点求解函数内置，将计算方法隐藏）。信息隐藏在此处的体现并不明显。接口设计部分则分为三类，一类将需要用到的运算符重载，一类提供运算方法对交点求解，以及和UI对接的接口，重点放在UI对接接口上，为此我们和合作小组进行了讨论，并决定最终的接口设计。
至于松耦合部分，由于核心代码的每个类仅有其固有的计算方法与属性，实际情况下对类中代码进行修改也并不会影响到其他类或是对代码进行整体大幅度改动。

对于更为复杂的软件工程项目，上述三种方法会有更大的发挥空间。

4.计算模块接口的设计与实现过程

计算模块接口的设计与实现过程。设计包括代码如何组织，比如会有几个类，几个函数，他们之间关系如何，关键函数是否需要画出流程图？说明你的算法的关键（不必列出源代码），以及独到之处。（7'）

与上次作业类似，本次作业里只有三个类(点/向量、线、圆)及其公共常用函数以及三个求解函数（具体UML图见下问），在类中只需对应属性以及提供向量计算的相关函数，并在三个求解函数中对类的交点进行求解。

求解函数的关键代码如下：

其中line.isOnLine()是判断点是否在线段/射线上的简单方法，其实现则是根据直线/线段/射线的向量方程 l = u + tv ，u是直线上一点，v是方向向量，t是系数，计算出t则易判断是否在所给线上。

void lineIntersectLine(const Line& l1, const Line& l2)
{
	if (dcmp(l1.v ^ l2.v) == 0)	return;
	Vector u = l1.p - l2.p;
	double t = (l2.v ^ u) / (l1.v ^ l2.v);

	Point temp = l1.p + l1.v * t;
	if (l1.type != "L" && !l1.isOnLine(temp))	return;
	if (l2.type != "L" && !l2.isOnLine(temp))	return;

	try {
		points.insert(temp);
	}
	catch(exception e){}
}

void lineIntersectCircle(const Line& L, const Circle& C)
{
	double t1, t2;
	double a = L.v.x, b = L.p.x - C.c.x, c = L.v.y, d = L.p.y - C.c.y;
	double e = a * a + c * c, f = 2 * (a * b + c * d), g = b * b + d * d - C.r * C.r;
	double delta = f * f - 4 * e * g;
	if (dcmp(delta) < 0)    return; //线圆相离
	if (dcmp(delta) == 0) {		    //线圆相切
		t1 = t2 = -f / (2 * e);
		if (L.type != "L" && !L.isOnLine(t1))	return;
		try {
			points.insert(L.point(t1));
		}
		catch (exception e) {
		}
		return;
	}
	//线圆相交
	t1 = (-f - sqrt(delta)) / (2 * e);
	t2 = (-f + sqrt(delta)) / (2 * e);
	Point p1 = L.point(t1);
	Point p2 = L.point(t2);
	if (L.type != "L" && !L.isOnLine(p1));
	else {
		try {
			points.insert(p1);
		}
		catch (exception e) {
		}
	}

	if (L.type != "L" && !L.isOnLine(p2));
	else {
		try {
			points.insert(p2);
		}
		catch (exception e) {
		}
	}
	return;
}

void circleIntersectCircle(const Circle& c1, const Circle& c2)
{
	double d = Length(c1.c - c2.c);
	if (dcmp(d) == 0) return; //两圆重合
	if (dcmp(c1.r + c2.r - d) < 0)    return;
	if (dcmp(fabs(c1.r - c2.r) - d) > 0)    return;
	double a = angle(c2.c - c1.c);
	double da = acos((c1.r * c1.r + d * d - c2.r * c2.r) / (2 * c1.r * d));
	Point p1 = c1.point(a - da), p2 = c1.point(a + da);
	try {
		points.insert(p1);
	}
	catch (exception e) {
	}
	if (p1 == p2)	return;
	try {
		points.insert(p2);
	}
	catch (exception e) {
	}
}

独到之处在于：用计算几何的方法，简洁高效的解决了核心代码的拓展部分。

5.UML类图

阅读有关 UML 的内容：https://en.wikipedia.org/wiki/Unified_Modeling_Language。画出 UML 图显示计算模块部分各个实体之间的关系（画一个图即可）。（2’）

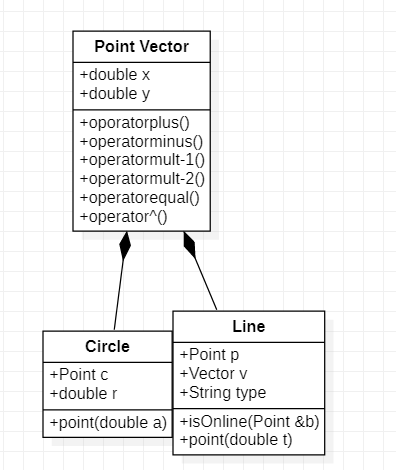
6.计算模块接口部分的性能改进

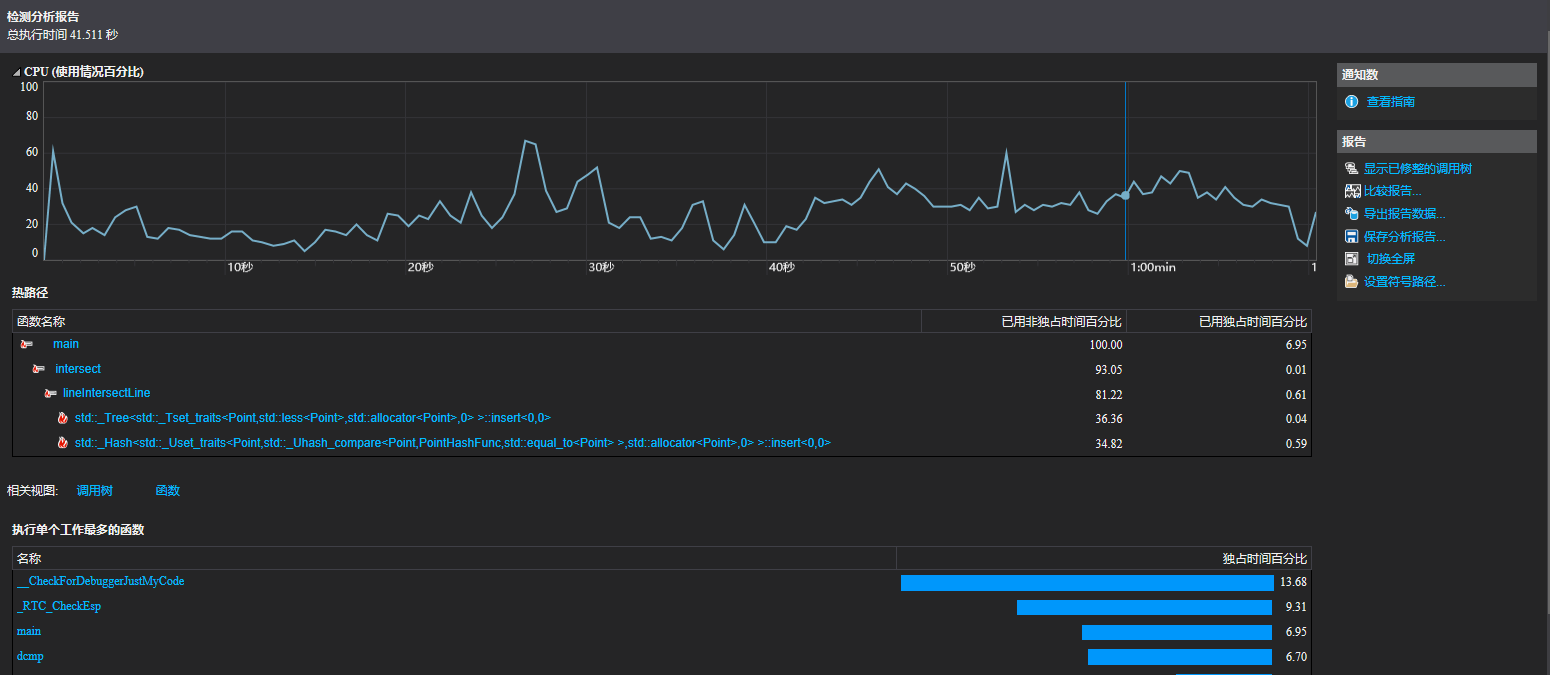
计算模块接口部分的性能改进。记录在改进计算模块性能上所花费的时间，描述你改进的思路，并展示一张性能分析图（由VS 2015/2017的性能分析工具自动生成），并展示你程序中消耗最大的函数。（3'）

性能改进方面依然没有想出更优复杂度的算法，只能够进行一些细节上的优化。由于C++的set是基于红黑树实现的，插入操作的复杂度为O（logn），所以考虑了换成基于哈希表实现的unordered_set, 在哈希函数理想的情况下，插入操作的复杂度为O(1)。换了unordered_set之后性能确实有了提升，在1000条直线，400000个交点的情况下，所用时间从9秒左右提升到了6秒左右。

7.Design by Contract/Code Contract

http://en.wikipedia.org/wiki/Design_by_contract

http://msdn.microsoft.com/en-us/devlabs/dd491992.aspx

描述这些做法的优缺点，说明你是如何把它们融入结对作业中的。（5'）

DBC通过（内建的或附加的）语言特性强制程序的前条件（pre- condition）、后条件（post-condition）、不变式（invariant）得到保证，并从而使程序接口得到进一步的明确。

其优点在于：

（1）明确接口功能，对程序的预期行为做检查，便于调试、发现程序中的错误；

（2）明确接口用途，编写者和使用者都可以得到足够的信息。

（3）便于代码重用。

（4）检测时间相对较短。

缺点在于：

（1）书写过于复杂，消耗时间过长。

在面向对象课程中，曾使用并编写过Java中的JML。在本次课程中，该点的体现主要在于核心代码与UI交接接口的设计上。UI模块只依赖于核心代码的接口函数和容器即可完成绘制任务。

8.计算模块部分单元测试展示

计算模块部分单元测试展示。展示出项目部分单元测试代码，并说明测试的函数，构造测试数据的思路。并将单元测试得到的测试覆盖率截图，发表在博客中。要求总体覆盖率到 90% 以上，否则单元测试部分视作无效。（6'）

在构造测试数据时，两两组合，分为L_L，R_R, S_S, L_R, L_S, L_C, R_S, R_C, S_C, C_C十种情况。

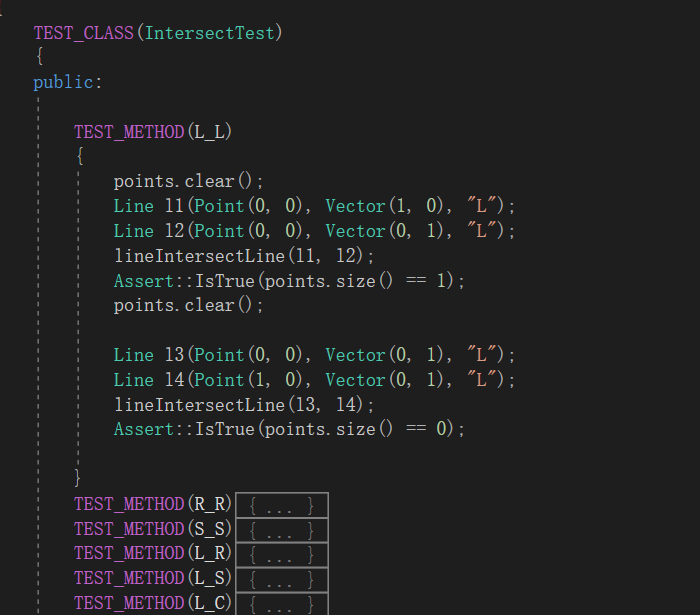
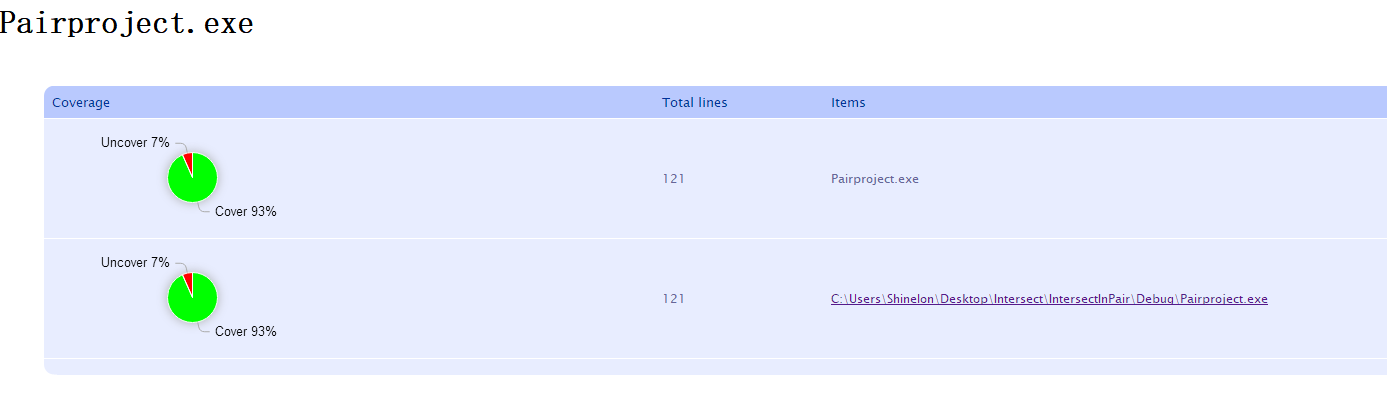
首先把能想到的情况进行了测试，比如直线相交，直线平行，射线端点，直线与圆相交，相切，相离等情况，然后根据覆盖率工具显示的未覆盖的分支，再添加对应的测试数据。

测试覆盖率：

9.计算模块部分异常处理说明

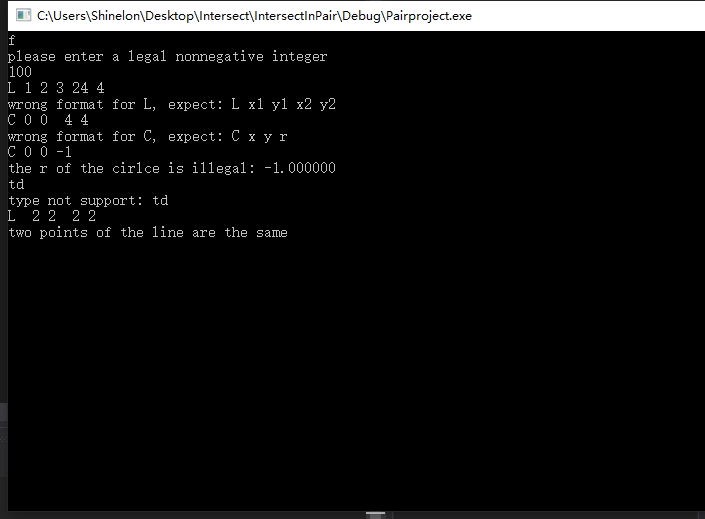
在博客中详细介绍每种异常的设计目标。每种异常都要选择一个单元测试样例发布在博客中，并指明错误对应的场景。（5'）

只设计了一个异常类，定义了五种异常类型。
WRONGTYPE: 输入了L, R, S, C之外的不支持的类型。
WRONGFORMAT: 输入了不符合规范的格式。
BADPOINT: 输入的点的坐标不在（-100000，100000）范围内。
BADLINE: 输入的直线的两个端点重合。
BADCIRCLE: 输入的圆的半径r小于等于0。

10.界面模块的详细设计过程

界面模块的详细设计过程。在博客中详细介绍界面模块是如何设计的，并写一些必要的代码说明解释实现过程。（5'）

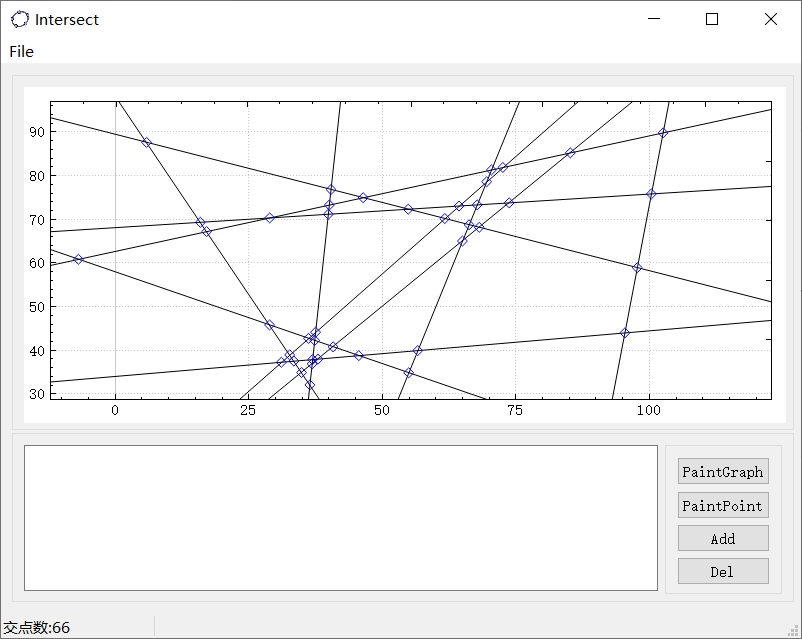
首先决定采用基于C++的QT编写UI，在资料查询的过程中，我发现了QT的第三方库QcustomPlot，看完其基本演示后，发现能够较为简单的实现类似GeoGebra的界面放缩和绘制功能，因此决定以QT+QcustomPlot完成UI任务。在阅读完《Qt5.9 c++开发指南》的前四章以及第七章IO处理之后，我认为已有的知识已经足够了，因此开始查询QcustomPlot官方文档以及答疑，同时进行UI代码编写。

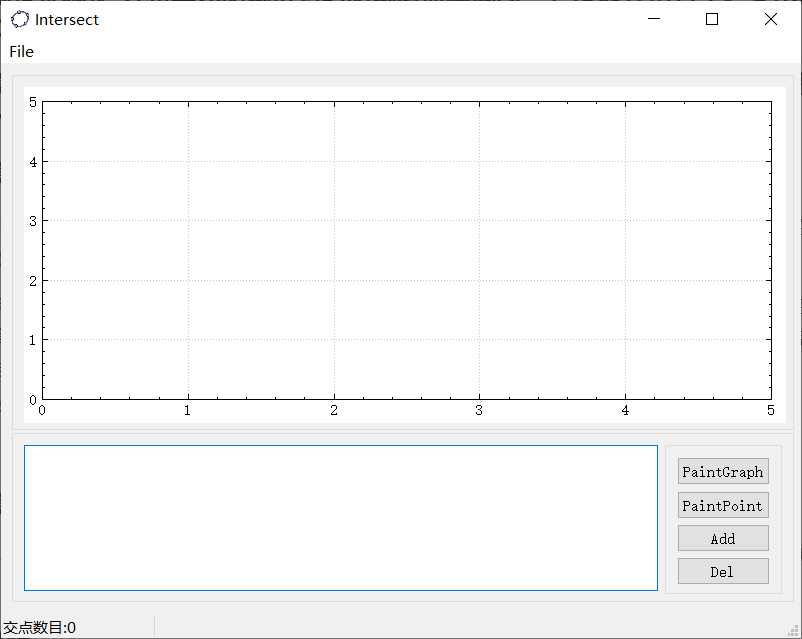
UI界面如上，共有四个Button（分别负责绘制图像、交点、添加、删除，其中添加删除格式与输入格式一致，例如“L 0 0 1 1”），一条menubar(负责打开文本文件),一个TextEdit(负责显示文本文件以及输入)，一个结果Lable(显示交点数目)，以及QcustomPlot区域（绘图），由于QT是可以可视化拖动模块并自动对其产生代码的，所以该部分的设计实现并不是人工的。

接着为了实现上述的功能，需要利用QT中的信号与槽机制，按钮的信号在其库中已有定义，需要写的是按钮按下后的反应，即按钮对应的槽，如下：

private slots:
    void on_actOpen_triggered();
    void on_AddBtn_clicked();
    void on_DelBtn_clicked();
    void on_PaintBtn_clicked();
    void on_PointBtn_clicked();

具体代码过长就不做展示了。这些槽函数定义了按钮的反应，Add和Del对应的是核心代码接口，这里主要讲两个绘制按钮的槽。

根据QcustomPlot官方文档可知其对圆，直线，射线，点均有多种不同实现方法，但大体而言分两类，一类在Graph对象中添加点集，形成图像；另一类AbstractItem则是直接对图像进行绘制（这里的原理并未细究，但其绘制速度是远超于点绘制的）。因此我编写了不同的绘制函数，如下：

    void paintPoint(QCustomPlot *customPlot,double x,double y);
    void paintLine(QCustomPlot *customPlot,double x1, double y1, double x2, double y2);
    void paintRay(QCustomPlot *customPlot,double x1, double y1, double x2, double y2);
    void paintSegment(QCustomPlot *customPlot,double x1, double y1, double x2, double y2);
    void paintCircle(QCustomPlot *customPlot,double x1, double y1, double x2, double y2);

经测试，在500000数量级的绘制下均可以保持使用流畅（当然，绘制需要时间，该库还提供了Opengl加速，但我并未实验）

11.界面模块与计算模块的对接

界面模块与计算模块的对接。详细地描述 UI 模块的设计与两个模块的对接，并在博客中截图实现的功能。（4'）

由于提前设计了接口

void add_diagram(char T, int x1, int y1, int x2, int y2);
void sub_diagram(char T, int a, int b, int c, int d);
void calPoints();
set<pair<double, double>> uiPoints;

因此在对接时只需要在四个按钮对应槽中合理调用接口即可。

实现的功能：

支持从文件导入几何对象的描述。

左上角File处可以添加文件，并显示在下方文本框中。
支持几何对象的添加、删除。

按下Add,Del按钮会添加/删除文本框中的集合对象
支持绘制现有几何对象。

PaintGraph按钮实现
支持求解现有几何对象交点并绘制。

PaintPoint按钮实现
坐标系放缩，平移（数量级10^-5 ~ 10^250）

12.结对过程

描述结对的过程，提供两人在讨论的结对图像资料（比如 Live Share 的截图）。关于如何远程进行结对参见作业最后的注意事项。（1'）

腾讯会议屏幕共享截图

日常微信交流截图

13.结对编程优缺点

看教科书和其它参考书，网站中关于结对编程的章节，例如：http://www.cnblogs.com/xinz/archive/2011/08/07/2130332.html ，说明结对编程的优点和缺点。同时描述结对的每一个人的优点和缺点在哪里（要列出至少三个优点和一个缺点）。（5'）

	结对编程	我	结对伙伴
优点	1.设计更好，Bug更少 2.在监督下可以更有效率地完成工作 3.两人共同解决困难问题，提高上限。	接受新知识较快；执行力较强；时间和任务管理较为到位。	能够仔细分析软件BUG；代码书写较快；思考较为全面
缺点	1.很多实际项目不适合结对编程；2.和结对伙伴的磨合结果会直接影响结对编程结果。	C++编码基础不够扎实。	交流不够主动

14. 附加题

代码支持圆（已实现，略）

松耦合

由于和对方团队（17373259 、 17373250 ）提前商量好了接口，因此模块的替换较为容易，基本无需更改。

将DLL替换后编码如下（以添加Add按钮为例）

 QString text = ui->textEdit->toPlainText();
    QFile outFile("./temp.txt");
    outFile.open(QIODevice::WriteOnly);
    QTextStream out(&outFile);
    for(int i = 0 ; i < text.size();i++){
        out << text.at(i);
    }
    outFile.close();

    QFile inFile("./temp.txt");
    inFile.open(QIODevice::ReadOnly);
    QTextStream in(&inFile);
    QChar sub;
    int x1,y1,x2,y2,r;
    QCustomPlot *customPlot = ui->qcustomPlot;
    while(in.atEnd() == false){
        in >> sub ;
        if(sub == "L")  {
            in >> x1 >> y1 >> x2 >> y2;
            add_diagram('L',x1,y1,x2,y2);
        }
        else if(sub == "R"){
            in >> x1 >> y1 >> x2 >> y2;
            add_diagram('R',x1,y1,x2,y2);
        }

        else if(sub == "S"){
            in >> x1 >> y1 >> x2 >> y2;
            add_diagram('S',x1,y1,x2,y2);
        }

        else if(sub == "C"){
            in >> x1 >> y1 >> r;
            add_diagram('C',x1,y1,r,0);
        }
    }
    ui->textEdit->clear();
    cout << point_map.size() << endl;

基本不需要修改源代码，即可完成dll更改。

一开始由于随机生成的测试样例中存在平行直线，出现了一些问题（己方dll是在QT中重新改写生成的，并未将核心代码中的错误处理部分导入，造成了这个测试样例中的问题未被及时发现）。后续修改后，经过测试，对方dll能够完成任务需求。

posted @ 2020-03-21 22:42 PandapanQAQ 阅读(368) 评论(2) 编辑收藏举报

刷新页面返回顶部

结对项目作业