二叉树c++实现
!!版权声明:本文为博主原创文章,版权归原文作者和博客园共有,谢绝任何形式的 转载!!
作者:mohist
--- 欢迎指正---
二叉树特点:
要么为空树;要么,当前结点的左孩子比当前结点值小,当前结点的右孩子比当前结点的值大。
1、插入:
1.1 插入结点的值比当前结点的值小,继续找当前结点的左子树,
1.2 插入结点的值比当前结点的值大,继续找当前结点的右子树,
1.3 找到合适的位置了,插入树。
2、删除:
2.1 删除结点是叶子结点,直接将其删除即可
2.2 删除结点只有左孩子或者只有右孩子,将其孩子结点删除,并将指向孩子结点的分支设置为空,c++是设置为NULL。不过更好的做法是,将孩子结点的值替换到当前结点,再删除孩子结点即可。
2.3 删除的结点同时含有左孩子与右孩子,需要找到删除结点的后继结点,将后继结点作为当前结点。
完整源码:
#include <iostream> using namespace std; struct node { // 数据域 int data; // 左节点 node *lc; // 右结点 node *rc; // 构造函数 node() : data(0) , lc(NULL) , rc(NULL) { } }; // bst class bstree { public: enum { hmax_size_32767 = 32767, hmin_size_0 = 0, }; public: // 构造函数 bstree() : root(NULL) , size(0) { } // 析构函数 virtual ~bstree(){} int get_size() { return size; } // 插入结点 void insert_node(int data) { int cur_size = get_size(); if (hmax_size_32767 == cur_size) { cout << "insert node error, the size of the tree is max" << endl; return ; } root = insert(root, data); } // 先序遍历(前序遍历) void pre_order() { pre_order_traverse(root); } // 中序遍历 void in_order() { in_order_traverse(root); } // 后序遍历 void post_order() { post_order_traverse(root); } /* 查找某个结点 int key - 查找结果 返回值: NULL : 可能为root为空 或者 没有找到 != NULL, 找到结点 */ node* query(int key) { if (NULL == root) { cout << "query error, root = null" << endl; return NULL; } return query_node(root, key); } // 删除树 void remove_all() { if (NULL == root) { cout << "remove all failed, root = null" << endl; return; } remove_all(root); int cur_size = get_size(); if (0 == cur_size) root = NULL; } // 删除某个结点 void remove_node(int del_data) { if (NULL == root) { cout << "remove node error, root = null" << endl; return; } node *parent_node = NULL; node *del_node = root; // 找到删除结点的父节点与删除结点 while (del_node) { if (del_data == del_node->data) break; else if (del_data > del_node->data) { parent_node = del_node; del_node = del_node->rc; } else if (del_data < del_node->data) { parent_node = del_node; del_node = del_node->lc; } } // 若没有找到要删除的结点 if (NULL == del_node) { cout << "remove node error, " << del_data << " was not find" << endl; return; } // 1、若删除的结点没有左子树和右子树 if ( (NULL == del_node->lc) && (NULL == del_node->rc) ) { // 为什么要先判断根结点,因为根结点的父节点找不到,结果为NULL, // 1.1 可能只有一个根结点, 将root释放值为空 if (del_node == root) { root = NULL; delete del_node; del_node = NULL; dec_size(); return; } // 1.2 非根结点,那就是叶子结点了, 将父节点指向删除结点的分支指向NULL if (del_node == parent_node->lc) parent_node->lc = NULL; else if (del_node == parent_node->rc) parent_node->rc = NULL; // 释放结点 delete del_node; del_node = NULL; dec_size(); } // 2、若删除结点只有左孩子,没有右孩子 else if ( (NULL != del_node->lc) && (NULL == del_node->rc) ) { // 2.1 删除结点为根结点,则将删除结点的左孩子替代当前删除结点 if (del_node == root) { root = root->lc; } // 2.2 其他结点,将删除结点的左孩子作为父节点的左孩子 else { if (parent_node->lc == del_node) parent_node->lc = del_node->lc; else if (parent_node->rc == del_node) parent_node->rc = del_node->lc; } delete del_node; del_node = NULL; dec_size(); } // 3、若删除结点只有右孩子 else if ( (NULL == del_node->lc) && (NULL != del_node->rc) ) { // 3.1 若为根结点 if (root == del_node) { root = root->rc; } else { if (del_node == parent_node->lc) parent_node->lc = del_node->rc; else if (del_node == parent_node->rc) parent_node->rc = del_node->rc; } delete del_node; del_node = NULL; dec_size(); } // 4、若删除结点既有左孩子,又有右孩子,需要找到删除结点的后继结点作为根结点 else if ( (NULL != del_node->lc) && (NULL != del_node->rc) ) { node *successor_node = del_node->rc; parent_node = del_node; while (successor_node->lc) { parent_node = successor_node; successor_node = successor_node->lc; } // 交换后继结点与当前删除结点的数据域 del_node->data = successor_node->data; // 将指向后继结点的父节点的孩子设置后继结点的右子树 if (successor_node == parent_node->lc) parent_node->lc = successor_node->rc; else if (successor_node == parent_node->rc) parent_node->rc = successor_node->rc; // 删除后继结点 del_node = successor_node; delete del_node; del_node = NULL; dec_size(); } } // 返回以proot为根结点的最小结点 node *get_min_node(node *proot) { if (NULL == proot->lc) return proot; return get_min_node(proot->lc); } // 返回以proo为根节点的最大结点 node *get_max_node(node *proot) { if (NULL == proot->rc) return proot; return get_max_node(proot->rc); } // 返回根节点 node *get_root_node() { return root; } // 返回proot结点的父节点 node *get_parent_node(int key) { // 当前结点 node *cur_node = NULL; // 父节点 node *parent_node = NULL; cur_node = root; // 标记是否找到 bool is_find = false; while (cur_node) { if (key == cur_node->data) { is_find = true; break; } // 因为比当前结点的值还要小,所以需要查找当前结点的左子树 else if (key < cur_node->data) { parent_node = cur_node; cur_node = cur_node->lc; } // 同上, 查找当前结点的右子树 else if (key > cur_node->data) { parent_node = cur_node; cur_node = cur_node->rc; } } return (true == is_find)? parent_node : NULL; } private: //查找某个值 node *query_node(node *proot, int key) { if (NULL == proot) { return proot; } if (proot->data == key) return proot; else if (proot->data > key) { return query_node(proot->lc, key); } else if (proot->data < key) { return query_node(proot->rc, key); } return NULL; } // 后序遍历删除所有结点 void remove_all(node *proot) { if (NULL != proot) { remove_all(proot->lc); remove_all(proot->rc); delete proot; dec_size(); } } // 先序遍历 void pre_order_traverse(node *proot) { if (NULL != proot) { cout << proot->data << ", "; pre_order_traverse(proot->lc); pre_order_traverse(proot->rc); } } // 中序遍历 void in_order_traverse(node *proot) { if (NULL != proot) { in_order_traverse(proot->lc); cout << proot->data << ", "; in_order_traverse(proot->rc); } } // 后续遍历 void post_order_traverse(node *proot) { if (NULL != proot) { post_order_traverse(proot->lc); post_order_traverse(proot->rc); cout << proot->data << ", "; } } // 插入结点 node *insert(node *proot, int data) { // 结点不存在, 则创建 if (NULL == proot) { node *new_node = new(std::nothrow) node; if (NULL != new_node) { new_node->data = data; proot = new_node; // 结点+1; add_size(); } return proot; } // 插入值比当前结点值还要小, 则应该插入到当前节点的左边 if (proot->data > data) { proot->lc = insert(proot->lc, data); } // 插入之比当前结点值还要打,则应该插入到当前结点的右边 else if (proot->data < data) { proot->rc = insert(proot->rc, data); } // 相等,则不插入结点。 return proot; } // size + 1 void add_size() { if (hmax_size_32767 == size) return ; size++; } // size - 1 void dec_size() { if ( hmin_size_0 == size) { return ; } size--; } private: // 根结点 node *root; // 当前树的结点个数 int size; }; // 测试代码 int main() { bstree tree; // tree.insert_node(50); tree.insert_node(30); tree.insert_node(10); tree.insert_node(0); tree.insert_node(20); tree.insert_node(40); tree.insert_node(70); tree.insert_node(90); tree.insert_node(100); tree.insert_node(60); tree.insert_node(80); // 前序遍历 cout << "前序遍历" << endl; tree.pre_order(); cout << endl; // 中序遍历 cout << "中序遍历" << endl; tree.in_order(); cout << endl; // 后序遍历 cout << "后序遍历" << endl; tree.post_order(); cout << endl; cout << "删除结点开始,结束请输入10086" << endl; int del_key = 0; while (true) { cout << "输入删除结点值 = "; cin >> del_key; if (10086 == del_key) break; tree.remove_node(del_key); cout << "删除后,结点个数 = " << tree.get_size() << endl; cout << "删除后, 中序遍历结果:" ;// << endl; tree.in_order(); cout << endl << endl; } tree.remove_all(); return 0; }
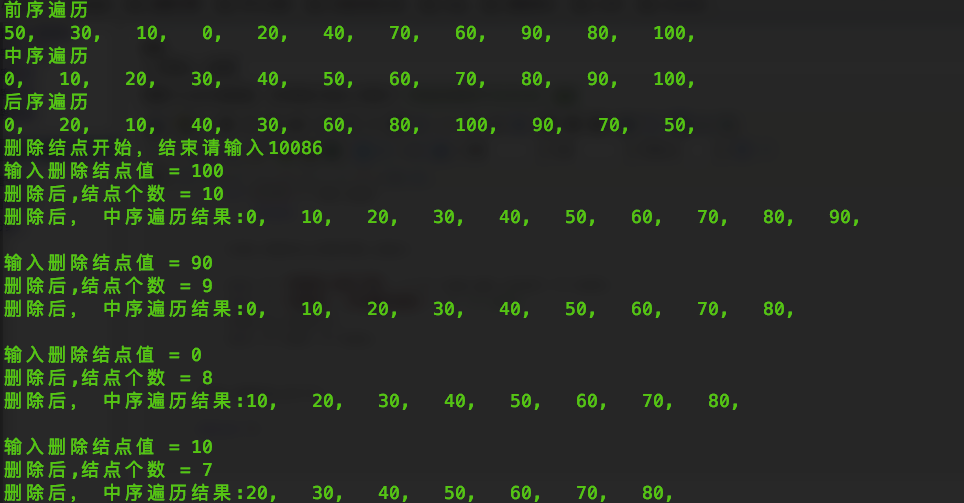
测试结果: