【数据分析师 Level 1 】19.时间序列

【数据分析师 Level 1 】19.时间序列

趋势分解法

时间序列预测技术就是通过对预测目标自身时间序列的处理，来研究其变化趋势的。一个时间序列往往是一下几类变化形式的叠加或耦合。

• 长期趋势变动：是指时间序列朝着一定的方向上持续上升或下降，或停留在某一水平上的倾向，它反映了客观事物的主要变化趋势；
• 季节变动：是指季度或月度的周期变化
• 循环变动：通常是指周期为一年以上，由非季节因素引起的涨落起伏波形相似的波动；
• 不规则变动：通常它分为突然变动和随机变动。

如图所示，黑色的曲线代表时间序列的原始取值，而根据原始序列的时间走势就能确定该时间序列的长期趋势变动。而很多行业都是存在季节性变动的趋势的。比如，运输行业、风力发电行业。又比如，水果和蔬菜价格等。而循环趋势也成为周期趋势。比如经济周期趋势。相对而言，循环和季节性趋势是原始序列中较为稳健的趋势变动。而无规则的随机趋势是难以进行预测的，且波动较大。因此，对于时间序列的拆分，通常是将较为稳健的长期循环以及季节性趋势拆分出来，而不考虑随机趋势的影响。

通常用

\[T_t \]

表示长期趋势项，

\[S_t \]

表示季节变动趋势项，

\[C_t \]

表示循环变动趋势项，

\[R_t \]

表示随机干扰项。

常见的确定性时间序列模型有以下3中类型。

• 加法模型

• \[Y_t = T_t + S_t + C_t +R_t \]

• 乘法模型（实际使用更多）

• \[Y_t = T_t \times S_t \times C_t \times R_t \]

• 混合模型

• \[Y_t = T_t \times S_t+R_t \]

  其中

  \[Y_t \]

  是观测目标的观测记录，且

  \[E(R_t) = 0,E = (R^2_t) = \sigma^2 \]

  如果在预测时间范围以内，没有突然变动且随机变动的方差较小，并且有理由认为过去和现在的演变趋势将持续发展到未来时，可用一些经验方法进行预测，具体方法如下

ARMA模型（平稳序列）

自回归模型AR（n）

假设时间序列

\[X_t \]

仅与

\[X_{t-1},X_{t-2},...,X_{t-n} \]

有线性关系。

而在

\[X_{t-1},X_{t-2},...,X_{t-n} \]

已知条件下，

\[X_t \]

与

\[X_{t-j}(j=n+1,n+2) \]

无关，

\[\epsilon_t \]

是一个独立于

\[X_{t-1},X_{t-2},...,X_{t-n} \]

的白噪声序列

\[X_t = \alpha_1X_{t-1}+\alpha_2X_{t-2}+...+\alpha_nX_{t-n}+\epsilon_t \]

其中

\[\epsilon_t \backsim N(0,\sigma^2) \]

事实上，AR模型就是从线性回归演化而来，只是线性回归是建立自变量X也因变量Y的线性关系，而向量自回归是建立当期

\[X_t \]

与往期

\[X_{t-n} \]

的线性关系。举个例子：某个电商的年销量呈现出

\[X_t = 276+0.6X_{t-1}+\epsilon_t \]

也就是今年的销量可以用去年的销量进行线性表示，这就是典型的AR。

移动平均模型MA（n）

如果一个系统在t时刻的响应

\[X_t \]

与其以前时刻

\[t-1,t-2,... \]

的响应

\[X_{t-1},X_{t-2},... \]

无关，而与其以前时刻

\[t-1,t-2,...,t-m \]

进入系统的扰动

\[\epsilon_{t-1},\epsilon_{t-2},...,\epsilon_{t-m} \]

存在一定的依存关系，那么这类系统成为MA（m）系统。

\[X_t = \beta_0\epsilon_t+\beta_1\epsilon_{t-1}+...+\beta_m\epsilon_{t-m} \]

其中

\[\epsilon_t \]

是白噪声过程。

自回归移动平均模型

一个系统如果在时刻t的响应，不仅与其以前时刻的自身值有关，而且还与其以前时刻进入系统的扰动存在一定的依存关系，那么，这个系统就是自回归移动平均系统ARMA（n，m）模型

\[X_{t}-\alpha_1X_{t-1}-\alpha_2X_{t-2}-,...-\alpha_nX_{t-n} = \beta_0\epsilon_t+\beta_1\epsilon_{t-1}+...+\beta_m\epsilon_{t-m} \]

其中，

\[\epsilon_t \]

是白噪声过程

对于平稳系统来说，由于AR、MA、ARMA（n，m）模型都是ARMA（n，m）模型的特例，我们以ARMA（n，m）模型为一般形式来建立时序模型。

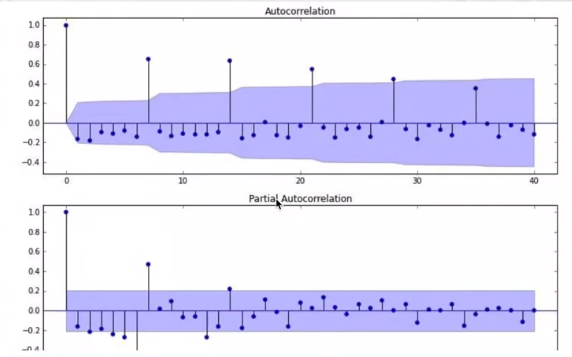
平稳时间序列的模型识别

• 根据自相关函数与偏自相关函数定阶
• 根据样本自相关函数和样本偏自相关函数定阶一般要求样本长度大于50，才能后一定的精确程度。

自相关函数和样本偏自相关函数定阶的准则：

	MA（q）	AR（p）	ARMA（p，q）
自相关函数	q步截尾	拖尾	拖尾
偏自相关函数	拖尾	p步截尾	拖尾

ARIMA模型

差分运算

差分运算是一种非常简便、有效的确定性信息提取方法，Cramer分解定理在理论上保证了适当阶数的差分一定可以充分提取确定性信息。差分运算的实质是使用自回归的方式提取确定性信息。

• 一阶差分：

• \[\nabla x_t = x_t - x_{t-1},(t=2,3,...) \]

• 二阶差分：

• \[\nabla^2{x_t} = \nabla{x_t}-\nabla{x_{t-1}} \]

• d阶差分：

• \[\nabla^d_{x_t} = \nabla(\nabla^{d-1}{x_t})=(1-B^d)x_t = \sum^d(-1)C^i_{d}x_{t-i} \]

• 其中B为后移算子，差分与后移算子的关系为

• \[\nabla = 1-B \]

差分方式的选择

序列蕴含着显著的线性趋势，一阶差分就可以实现趋势平稳；序列蕴含着曲线趋势，通常低阶（二阶或三阶）差分就可以提取出曲线趋势的影响。对于蕴含着固定周期的序列，进行步长为周期长度s的差分运算（季节差分），通常可以较好地提取周期信息，如季节差分和D阶季节差分：

\[\nabla_{s}x_t = x_t-x_{t-s}(2,3,...) \\ \nabla^D_sx_t = \nabla_s(\nabla^{D-1}_sx_t) \]

足够多次的差分运算可以充分地提取原序列中的非平稳确定性信息，但过度的差分会造成有用信息的浪费。

一般步骤：

（1）平稳性检验。在这个环节中，我们需要对数据进行平稳性检验，这是因为只有平稳的序列，其特征才是稳定的，可重复的，也就具有了预测的可能性。如果序列本身是非平稳的，那么通常我们有两种处理方式，一是进行差分，二是进行对数变换。

（2）对于平稳的序列，我们需要对计算序列的ACF和PACF，通过分析ACF和PACF拖尾和截尾的形态，来判断ARIMA模型的形式以及p和q的取值（由于考虑差分已经使得序列平稳了，所以事实上对平稳的序列，ARIMA就等同于ARMA）

注意

如果自相关函数ACF在n阶之后迅速趋近于零，我们称ACF具有n阶截尾性；反之，如果自相关函数ACF不能在某一阶之后迅速趋近于零（截尾），而是按指数衰减（或成正弦波形式），我们则称其具有拖尾性。同理，PACF的截尾和拖尾具有相同的定义。

（3）模型识别。通过对于ACF和PACF拖尾与截尾形态，判断ARMA的具体形式（AR、MA或者ARMA）

（4）参数估计。对于已经确定的ARMA具体形式进行参数估计

（5）模型检验。这里主要是指对于残差进行检验，通常需要检验其独立性，以及期望方差为常数。

例题精讲

1.一个时间序列模型为

\[X_t = \beta_0\epsilon_t + \beta_1\epsilon_{t-1}+...+\beta_m\epsilon_{t-m} \]

其中

\[\epsilon_t \]

是白噪声过程，则

\[X_t \]

为：

A.宽平稳时间序列

B.自回归时间序列

C.非平稳时间序列

D.移动平均时间序列

答案：D

解析：从模型形式上来看，系统在t时刻的响应X_t与以前时刻进入系统的扰动存在一定的依存关系，根据定义，这样的模型称为移动平均模型，因此答案为D。在应用中要能够根据需求选择合适的时间序列模型，因此大纲中要求掌握的模型能够准确进行区分。

2.时间序列AR（p）模型，其中p指的是？

A.时间序列的自相关系数是P阶截尾的

B.时间序列的自相关系数是P阶拖尾的

C.时间序列的偏相关系数是P阶截尾的

D.时间序列的偏相关系数是P阶拖尾的

答案：C

解析：考核如果通过观察ACF和PACF图形，确定AR模型和MA的类型和滞后阶数，本题要求对模型参数和概念要熟知。