梯度下降算法在机器学习中的工作原理
梯度下降算法在机器学习中的工作原理
作者|NIKIL_REDDY
编译|VK
来源|Analytics Vidhya
介绍
梯度下降算法是工业中最常用的机器学习算法之一。但这让很多新人感到困惑。
如果你刚刚接触机器学习,梯度下降背后的数学并不容易。在本文中,我的目的是帮助你了解梯度下降背后的直觉。

我们将快速了解成本函数的作用,梯度下降的解释,如何选择学习参数。
什么是成本函数
它是一个函数,用于衡量模型对任何给定数据的性能。成本函数将预测值与期望值之间的误差量化,并以单个实数的形式表示出来。
在对初始参数进行假设后,我们计算了成本函数。以降低代价函数为目标,利用梯度下降算法对给定数据进行参数修正。下面是它的数学表示:
_LI.jpg)
什么是梯度下降
假设你在玩一个游戏,玩家在山顶,他们被要求到达山的最低点。此外,他们还蒙着眼睛。那么,你认为怎样才能到达湖边?
在你继续读之前,花点时间考虑一下。
最好的办法是观察地面,找出地面下降的地方。从这个位置开始,向下降方向迈出一步,重复这个过程,直到到达最低点。
梯度下降法是一种求解函数局部极小值的迭代优化算法。
要用梯度下降法求函数的局部极小值,必须选择与当前点处函数的负梯度(远离梯度)的方向。如果我们采取与梯度的正方向,我们将接近函数的局部极大值,这个过程称为梯度上升。
梯度下降最初是由柯西在1847年提出的。它也被称为最速下降。
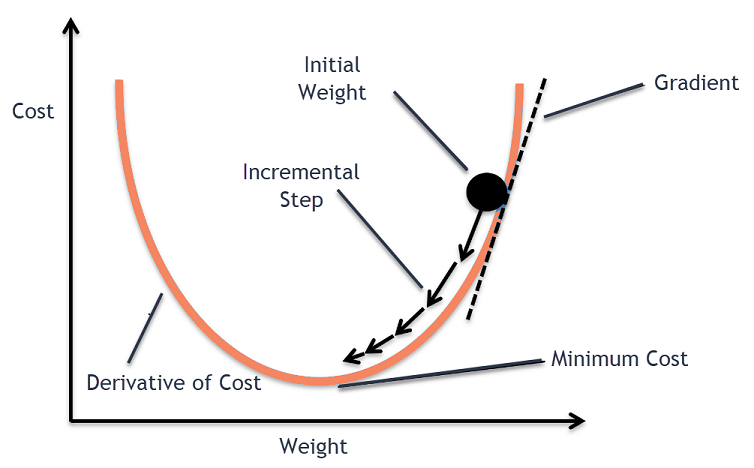
梯度下降算法的目标是最小化给定函数(比如成本函数)。为了实现这一目标,它迭代地执行两个步骤:
-
计算梯度(斜率),函数在该点的一阶导数
-
在与梯度相反的方向上做一步(移动)
.png)
Alpha被称为学习率-优化过程中的一个调整参数。它决定了步长。
绘制梯度下降算法
当我们有一个单一的参数(θ),我们可以在y轴上绘制因变量成本,在x轴上绘制θ。如果有两个参数,我们可以进行三维绘图,其中一个轴上有成本,另两个轴上有两个参数(θ)。

它也可以通过使用等高线来可视化。这显示了一个二维的三维绘图,其中包括沿两个轴的参数和等高线的响应值。远离中心的响应值增加,并且随着环的增加而增加。

α-学习率
我们有了前进的方向,现在我们必须决定我们必须采取的步骤的大小。
必须谨慎选择,以达到局部最小值。
-
如果学习率太高,我们可能会超过最小值,而不会达到最小值
-
如果学习率太低,训练时间可能会太长

a) 学习率最优,模型收敛到最小
b) 学习速度太小,需要更多的时间,但会收敛到最小值
c) 学习率高于最优值,较慢速度的收敛(1/c<η < 2/c)
d) 学习率非常大,它会过度偏离,偏离最小值,学习性能下降

注:随着梯度减小而向局部最小值移动,步长减小。因此,学习速率(alpha)可以在优化过程中保持不变,而不需要迭代地改变。
局部最小值
成本函数可以由许多最小点组成。梯度可以落在任何一个极小值上,这取决于初始点(即初始参数θ)和学习速率。因此,在不同的起点和学习率下,优化可以收敛到不同的点。

梯度下降的Python代码实现
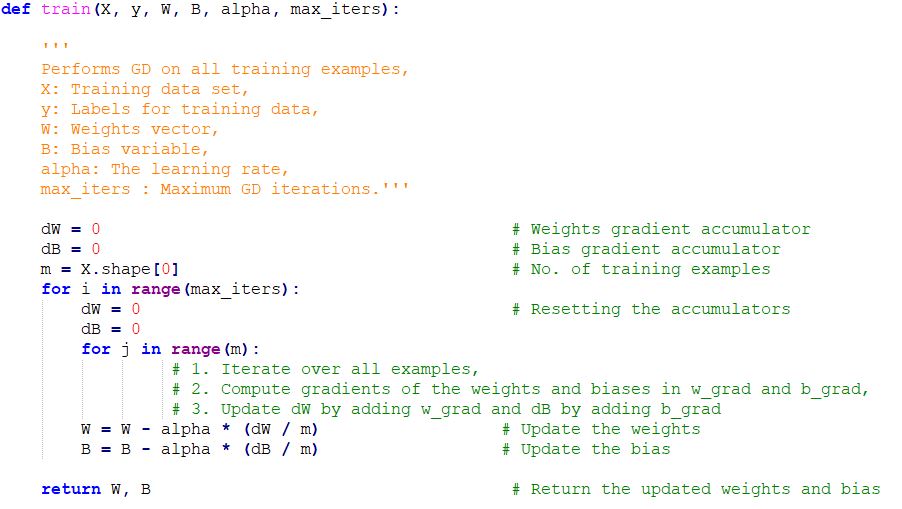
结尾
一旦我们调整了学习参数(alpha)并得到了最优的学习速率,我们就开始迭代,直到我们收敛到局部最小值。
欢迎关注磐创AI博客站:
http://panchuang.net/
sklearn机器学习中文官方文档:
http://sklearn123.com/
欢迎关注磐创博客资源汇总站:
http://docs.panchuang.net/



