C语言中的窗口滑动技术
学习文章:C语言中的窗口滑动技术
滑动窗口法
- C语言中的窗口滑动技术
循环几乎是每个复杂问题的一部分。太多的循环/嵌套循环会增加所需的时间,从而增加程序的时间复杂性。窗口滑动技术是一种计算技术,用于减少程序中使用的嵌套循环的数量,通过用单个循环代替嵌套循环来提高程序的效率。
如果你熟悉计算机网络中的滑动窗口协议,这种技术也很类似,本教程通过不同的例子解释了这种技术的使用方法。
一般来说,当我们使用这样的嵌套循环时 。
for(i = 1; i <= n; i++)
{
for(j = i; j < k; j++)
{
}
}
迭代: 外循环执行\(n\)次;每执行一次外循环,内循环就执行\((k-i)\)次。执行整个循环所需的平均时间大约为$O(N^2) $。因此,开发人员不建议使用循环。
让我们举一个例子来清楚地理解这个概念 。
假设我们要找到一个数组中\(’k’\)个连续元素的最大和,用户提供\(k\)值:
首先,如果我们使用传统的方法,对于数组中的每个元素\(i\),我们将从\(i+1\)到\(n-1\)遍历数组,其中\(n\)是数组的大小,我们需要对每个元素都这样做,然后比较总和,得到最大总和。
- 暴力方法
#include<stdio.h>
int main()
{
/*
找到一个数组中’k’个连续元素的最大和
*/
int n, size, sum=0, max = 0, j;
printf("Enter the size of the array: ");
scanf("%d", &n);
int arr[n], i;
printf("Enter the elements of the array: ");
for(i = 0; i < n; i++)
{
scanf("%d", &arr[i]);
}
printf("Enter the size of sub-array: ");
scanf("%d", &size);
for(i = 0; i < (n - size) + 1; i++)
{
/*
其实也是滑动窗口的思想
*/
sum = 0;
for(j = i; j < i + size; j++)
{
sum = sum + arr[j];
}
if(sum > max)
{
max = sum;
}
}
printf("The maximum sum of %d consecutive elements of the array: %d\n", size, max);
}
输出 :
Enter the size of the array: 10
Enter the elements of the array: 8 2 1 7 3 2 5 8 1 3
Enter the size of the sub-array: 3
The maximum sum of 3 consecutive elements of the array: 20
现在,滑动窗口技术来了
这里的概念是,我们创建一个大小为\(k\)的窗口,我们将通过一个单位指数不断地滑动它。在这里,窗口并不是什么技术术语。我们不是像在循环中那样使用一个单一的值,而是在每次迭代中同时使用多个元素。
比如说给定一个大小为10的数组:
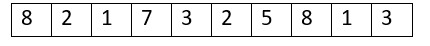
假设我们需要3个连续索引的最大和,创建一个3个大小的窗口,并在整个数组中不断滑动(遍历)它。这里有一个形象的表示。
迭代1:
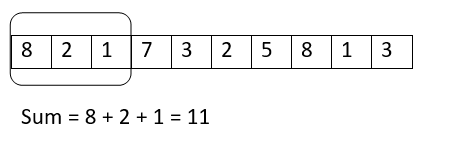
迭代2 :
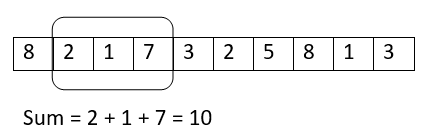
迭代3:
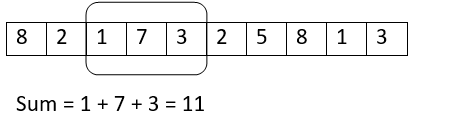
迭代4:
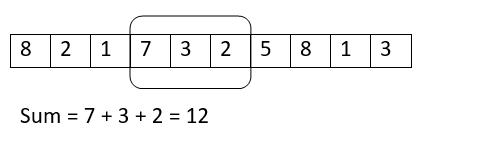
迭代5:
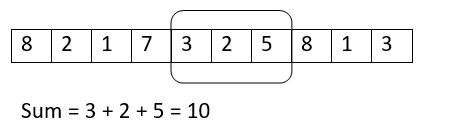
迭代6:
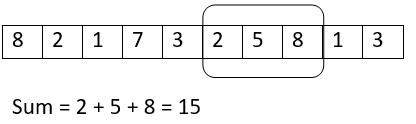
迭代7:
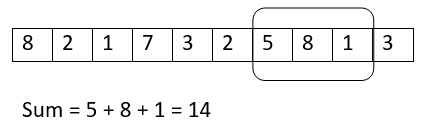
迭代8:
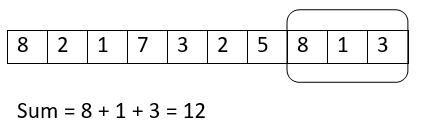
- 使用这种方法,将没有内循环,一个单循环的迭代次数将是\((n – k + 1)\),在这种情况下是8。
- 所以,滑动窗口是一种用于减少嵌套循环的技术,用一个单循环代替它,以减少总的时间复杂性。
- 请注意,在每次迭代中,当窗口滑动到下一个索引时, 我们都会删除前一个窗口的第一个元素,并添加一个新的元素,即下一个继任索引。
下面是代码:
#include <stdio.h>
int maxsum(int a[], int k, int n);
int main()
{
int n, i, k;
printf("Enter the size of the array: ");
scanf("%d", &n);
int arr[n];
printf("Enter the elements: ");
for (i = 0; i < n; i++)
{
scanf("%d", &arr[i]);
}
printf("Enter the value of k: ");
scanf("%d", &k);
int max = maxsum(arr, k, n);
printf("The maximum sum of %d consecutive elements in the array: %d\n", k, max);
}
int maxsum(int a[], int k, int n)
{
int i, sum, maxm = 0;
for (i = 0; i < k; i++)
{
maxm = maxm + a[i]; //记录第一个窗口元素和
}
sum = maxm; //初始化sum
for (i = k; i < n; i++)
{
sum += a[i] - a[i - k]; //当窗口滑动到下一个索引时, 我们都会删除前一个窗口的第一个元素,并添加一个新的元素
if (sum > maxm)
{
maxm = sum;
}
}
return maxm;
}
输出:
Enter the size of the array: 10
Enter the elements: 8 2 1 7 3 2 5 8 1 3
Enter the value of k: 3
The maximum sum of 3 consecutive elements in the array: 15
- 暴力方法在两个嵌套循环中需要\(O(k*n)\)时间。
- 通过使用滑动窗口技术,时间复杂度降低到\(O(n)\)。
以下是将该技术应用于手头任何问题的步骤:
- 首先,我们必须看到,窗口的大小是恒定的,不应该改变。我们可以只对这样的问题使用该技术。
- 在确保窗口大小没有变化后,计算第一个窗口的结果,与数组其他部分的计算结果进行比较。
- 现在,用一个循环来逐个滑动窗口的索引,直到最后,不断更新所需的值。
题目1

方法
- 双层循环【暴力破解】
我们需要两层循环,第一层循环遍历字符串、并且记录第二层循环开始的位置。
①创建一个新的数组;
②从第一个字符开始遍历,不重复的字符就将它放到新的数组中,遇到重复的就停止,计算该子串的长度;
③开始下一次循环,直到遍历到字符串结束。
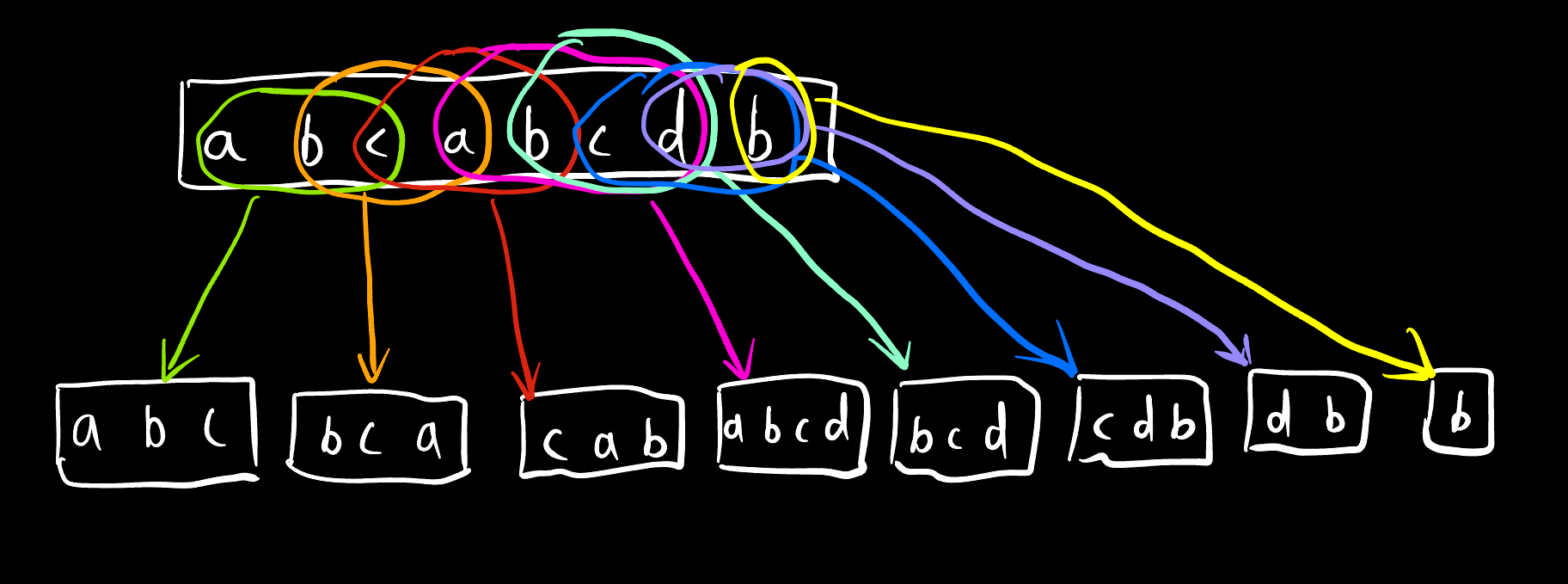
代码:C
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
int lengthOfLongestSubstring(char *s)
{
if (s == NULL) // 判断空指针
return 0;
int len = strlen(s);
int maxlength = 0; // 记录最长长度
int i = 0;
for (i = 0; i < len; i++) // 外层循环遍历字符串
{
int curlength = 0; // 记录每一次的长度
char *tmp = (char *)calloc(len, 1); // 用来存放子串
int t = 0;
int j = i; // 从i开始遍历
while (s[j] && !strchr(tmp, s[j])) // 要防止子串出现越界情况
{
tmp[t++] = s[j++]; // 字符不存在就保存
}
curlength = t; // 子串的长度
if (maxlength < curlength) // 找最长
{
maxlength = curlength;
}
free(tmp);
}
return maxlength;
}
int main()
{
char *s = "abcabcdb";
int k = lengthOfLongestSubstring(s);
printf("k=%d\n", k);
return 0;
}
- 滑动窗口法
上面暴力破解的时间复杂度很高:\(O(n^2)\),我们可以发现内循环每进行一次都会有数据被重复移动,这个操作消耗了大量的时间,在「C语言中的窗口滑动技术」中,我们了解滑动窗口法可以减少循环次数,提升程序效率,下面我们通过滑动窗口的方法来进行化简。
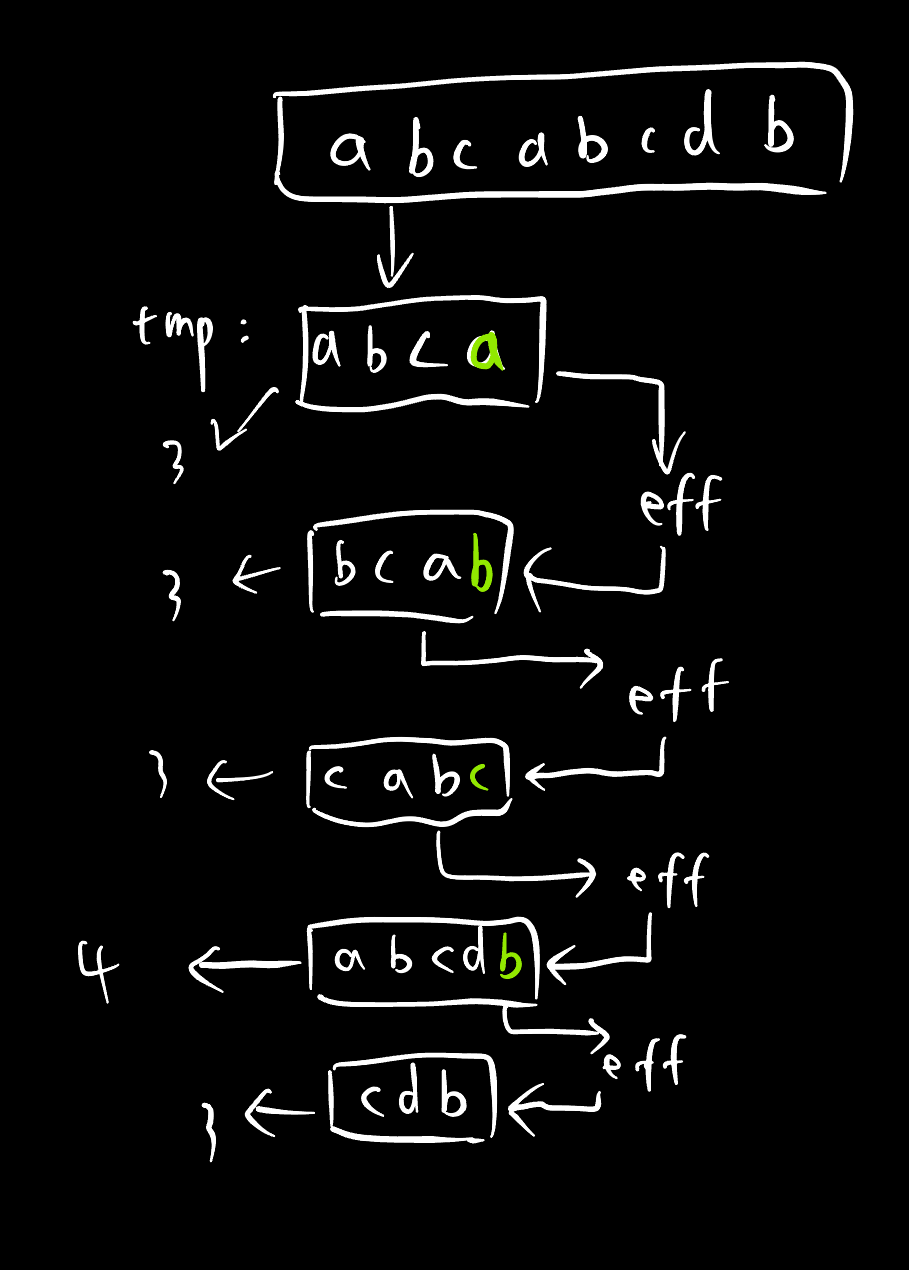
代码:C
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
int lengthOfLongestSubstring(char *s)
{
if (s == NULL)
return 0;
int len = strlen(s);
char *tmp = (char *)calloc(len, 1);
int right = 0; // 有效字符串长度
int maxlength = 0; // 记录最长长度
int i = 0;
for (i = 0; i < len; i++)
{
char *p = strchr(tmp, s[i]);
tmp[right] = s[i]; //先插入tmp
right++;
if (p) // 如果该字符已存在,就跳到该位置
{
right = right - (p - tmp) - 1; // 更新长度,指针相减(p - tmp)表示指针指向位置相隔的元素个数
char *eff = (char *)malloc(right);
// 跳过中间重复的部分
memcpy(eff, p + 1, right); // 先将有无重复的字符串保存
memset(tmp, '0', (p - tmp + 1 + right)); // 清空原字符串
memcpy(tmp, eff, right); // 将新字符串重新拷贝回去
free(eff);
}
if (maxlength < right) // 找最长
{
maxlength = right;
}
}
return maxlength;
}
int main()
{
char *s = "abcabcdb";
int k = lengthOfLongestSubstring(s);
printf("k=%d\n", k);
return 0;
}
- 滑动窗口法(改进)
上面我们通过字符的复制和删除来省略了多次遍历的过程,不过,我们在删除字符的时候需要将后面全部的字符都往前移,这样也浪费一些时间,那么我们是否可以通过找到最长子串的具体位置,来省去删除字符的过程呢?答案肯定是可以的,下面就让我们开始实际操作。
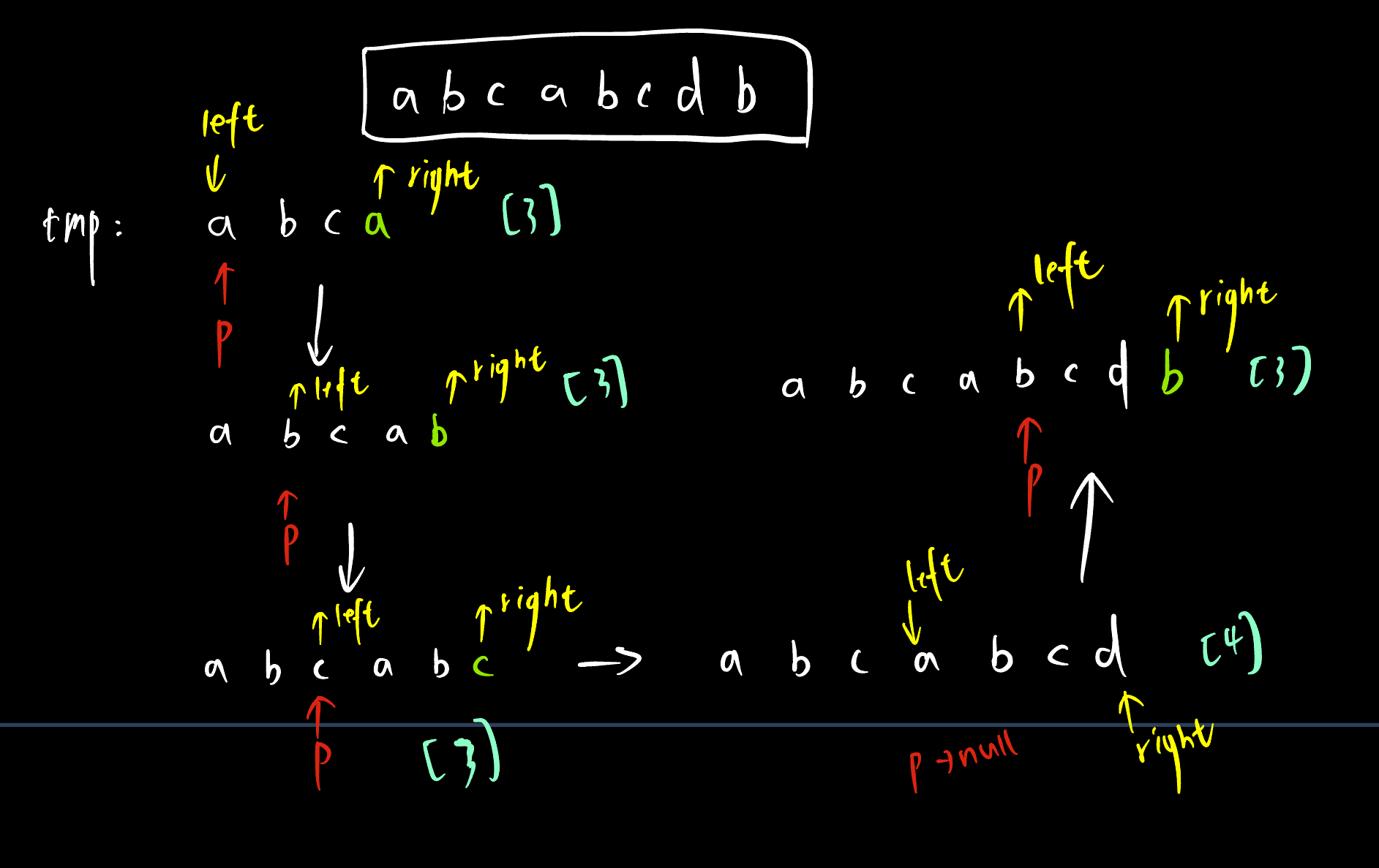
程序:C
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
int lengthOfLongestSubstring(char* s) {
if (s == NULL)
return 0;
int len = strlen(s);
char* tmp = (char*)calloc(len, 1);
int right = 0; // 当前字符串长度
int left = 0; // 控制子串起始位置
int maxlength = 0; // 记录最长长度
for (int i = 0; i < len; i++)
{
char* p = strchr(tmp + left, s[i]);//这里需要注意的一点是字符必须先判断后复制
tmp[right] = s[i]; //逐个遍历,存储
right++;
if (p) // 如果该字符已存在,就跳到前面重复字符的下一个位置
{
left = p - tmp + 1; //p指针后一位
}
int curlength = right - left; // 当前子串长度
if (maxlength < curlength)// 找最长
{
maxlength = curlength;
}
}
free(tmp);
return maxlength;
}
int main()
{
char *s = "abcabcdb";
int k = lengthOfLongestSubstring(s);
printf("k=%d\n", k);
return 0;
}
题目2

方法
题目要求找一段连续子数组,并且该子数组的和sum要\(>=\)target,那么我们首先就是要遍历数组求和,直到\(sum>=target\)。
下面我们直接使用滑动窗口的思想进行破题: 那么我们在这里会遇到哪些特殊情况呢?
-
特例1:整个数组的和都小于target,不过当窗口的右边界越界的时候我们已经跳出循环了,所以也就不需要再做特殊处理;
-
特例2:有一个数组元素特别大,我们减去前面的一个元素后,sum依然大于target,这时我们就需要先将sum的值不断减小之后才能继续扩大右边界。
程序:C
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
int minSubArrayLen(int target, int *nums, int numsSize)
{
int minlen = numsSize + 1; // 最短长度
int sum = 0; // 求和
int left = 0; // 记录左边界
int right = 0;
while (right < numsSize) // 右边界改变
{
sum += nums[right++]; // 这里需要更新right,否则结果会少一
while (sum >= target) // 特例1
{
minlen = minlen > right - left ? right - left : minlen;
sum -= nums[left++]; // 左下标需要右移
}
}
return minlen == numsSize + 1 ? 0 : minlen; // 特例2
}
int main()
{
int target = 7, nums[] = {2, 3, 1, 2, 4, 3};
int k = minSubArrayLen(target, nums, sizeof(nums) / sizeof(nums[0]));
printf("k=%d\n", k);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号