公钥密码复习
公钥密码复习
DH协议
1976年Diffie和Hellman首次提出公钥密码体制，并介绍了DH密钥协商协议，该协议基于离散对数问题，可以在一个两方的安全信道中协商出一个安全共享密钥，可解决对称加密中的密钥传输问题。
DH协议起初是在有限域上计算，即基于的是有限域上的离散对数问题。
有限域上的DH
- 即给定一个有限域\(G_p\)，其中\(g\)是生成元，参数\(p,g\)公开。
- 两方交互后各自计算出\(g^{ab}(mod p)\)，作为共享密钥。
- 安全性依赖于有限遇上的离散对数问题：即使敌手获取了\(g^a(mod p)\)或者\(g^b(mod p)\)，也不能得到\(a\)或者\(b\)。
下面介绍基于椭圆曲线（ECC）上离散对数问题的DH协议。
椭圆曲线上的DH
- 这里是由椭圆曲线上及上面的点构成的阿贝尔群\(E_p(a,b)\)，其中点$G(x_1,y_1)为群的生成元。
- 椭圆曲线的阶（即所有点，包括无穷远点）是一个很大的素数；生成元\(G\)的阶（即满足\(nG=O\)的最小正整数）是\(n\)。
- 两方交互后各自计算出\(n_An_BG\)作为共享密钥。
- 安全性依赖于椭圆曲线上的离散对数问题，即即使敌手获取了\(n_AG\)或者\(n_BG\)，也得不到\(n_A\)或者\(n_B\)。
下面举一个例子：
DH协议还可以扩展为多方，以三方为例：
扩展为多方
- 就是先各自计算出\(g^x,g^y,g^z\)，A发给B，B发给C，C再发给A。
- 再发送一次，各方得到\(g^{ayz}\)
多方DH，会随着人数增加，通信轮数迅速增加，因此不适合用于群密钥协商。
攻击方式
DH密钥协商不包含通信双方的身份认证，因此会受到中间人攻击，即敌手能截获替换的交互消息，从而监听通信内容。
- 中间人（敌手）可以获得\(g^{am}\)和\(g^{bm}\)，在接下来两方的加密通信中可以获取通信内容。
- 为了抵抗这种攻击，就是在通信中进行身份认证。
认证密钥协商
下面介绍一种DH秘钥协商协议的改进协议-端对端STS协议，即引入签名进行身份认证。
- 引入一个可信的CA，用于生成密钥。
- 两方在第一次交互后，需要将计算的消息签名后发送给对方。
- 收到后，先验证签名的有效性，再去计算最终的密钥。
RSA
1978年由Rivest，Shamir和Adleman提出的一种成熟的公钥加密方案，目前还在广泛应用，比如HTTPS中的加密。
RSA原方案：A Method for Obtaining Digital Signatures and Public-Key Cryptosystems-1978
因为RSA是一个公钥加密算法，密钥生成都是基于一个数学困难问题，即所谓的“只要给出一个数学困难问题，就能构造一个公钥加密算法”。
RSA算法基于的是大整数难分解问题，简单说就是：给定一个大整素数\(n=p*q\)，找出\(p\)和\(q\)是困难的。
加密方案
密钥生成
- 选取两个保密得大素数\(q\)和\(p\)
- 计算\(n=p*q\)，\(\varphi (n)=(p-1)*(q-1)\)，其中\(\varphi (n)\)是\(n\)的欧拉函数。（因为\(p\)和\(q\)都是素数）
- 选择一个整素数\(e\)，满足\(1<e<\varphi (n)\)，且\(gcd(\varphi (n),e)=1\)。（即\(\varphi (n)\)和\(e\)互素）
- 计算\(d\)，且满足\(d*e=1 mod \varphi (n)\)，即\(d=e^{-1}(mod \varphi (n))\)
- 所以形成公钥\((e,n)\)，私钥\((d)\)，在系统初始化后两个素数\(q\)、\(p\)和$ \varphi (n)$是可以销毁的，但不能泄漏
下面举一个例子说明：
加密
- 明文\(m\in M\)，\(M=\left \{ m|0<m<n \right \}\)是明文空间，若明文较大（大于\(n\)），即将明文按比特分组，使得每个分组对应的十进制数小于\(n\)，即分组长度小于\(log_2^n\)
- 加密函数\(E(m)=m^e(mod n)\)
- 计算出密文\(c=m^e(mod n)\)
解密
- 解密函数\(D(c)=c^d(mod n)\)
- 解密出明文\(m=c^d(mod n)\)
正确性
- \(c^d(mod n)=m^{ed}(mod n)=m^{k*\varphi (n)+1}(mod n)\)
- 分两种情况讨论：
- \(gcd(m,n)=1\)，由欧拉定理得：\(m^{\varphi (n)}=1(mod n),m^{k*\varphi (n)}=1(mod n),m^{k*\varphi (n)+1}=m(mod n)\)，即\(c^d(mod n)=m\)
- \(gcd(m,n)\neq 1\)，参考（现代密码学-杨波），也能证明\(c^d(mod n)=m\)。
安全性
RSA的安全性基于大整数难分解问题的假定，因为大整数难分解问题至今未能证明是NP问题。
大整数难分解问题：给定大整数\(n=p*q\)，难求出\(p,q\)。
在RSA方案中，因为根据\(n\)，难以求出\(p,q\)，也就难以求出\(\varphi (n)=(p-1)*)(q-1)\)，继而推不出私钥\(d=e^{-1}(mod \varphi (n))\)。
乘法同态
给定两个密文\(c_1=m_1^e(mod n),c_2=m_2^e(mod n)\)：
\(D(c_1*c_2)=D((m_1*m_2)^e(mod n)=(m_1*m_2)^{de}(mod n)=m_1*m_2\)
程序实现
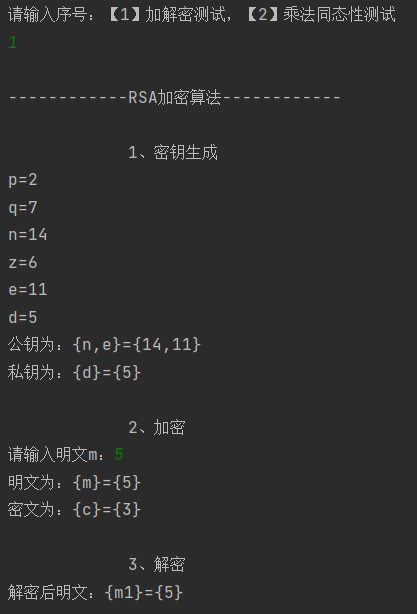
1、实现上述例子
只能实现小数计算
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#define randomInt(a,b) (rand()%(b-a)+a)//生成[a,b]之间的随机数
//是否为素数
int prime(int n)
{
int i;
if (n < 2) {
return -1;
}
else {
for (i = 2; i < n; i++) {//判断n在2~n-1中有没有因数
if (n % i == 0)//如果用可以除尽的数,则非素数
break;
}
if (i < n) {//存在2~n-1之间有因数
return -1;
}
else
return 0;
}
return 0;
}
//素数生成
int creat_Prime(int a,int b)
{
int res,k;
srand((unsigned)time(NULL));
do
{
res = randomInt(a, b);
k = prime(res);
} while (k == -1);
return res;
}
//求最大公约数，判断两个数是否互素
int gcd(int x, int y)
{
int t;
while (y) t = x, x = y, y = t % y;
return x;
}
//扩展欧几里得算法 （C++实现）
int exgcd(int a, int b, int &x, int &y)
{
if (b == 0)
{
x = 1, y = 0;
return a;
}
int ret = exgcd(b, a % b, y, x);
y -= a / b * x;
return ret;
}
//求逆元：基于费马定理
int reverse(int a, int mod)
{
int x, y;
int d = exgcd(a, mod, x, y);
return d == 1 ? (x % mod + mod) % mod : -1;
}
//快速幂模（a^b mod p)
int power(int a, int b, int p)
{
int ans = 1 % p;
while(b)
{
if(b & 1)
{
ans = ans * a % p;
}
b >>= 1;
a = a * a % p;
}
return ans;
}
//加密算法测试
void encrypt_test()
{
printf("\n------------RSA加密算法------------\n");
printf("\n\t 1、密钥生成\n");
//p和q是大素数;n=pq;z=(p-1)(q-1);任取e，使满足gcd(e,z)=1;d是e的逆;m是明文;c是密文;m1是解密后明文
int p, q, n, z, e, d, m, c, m1;
//随机生成p和q
p = creat_Prime(1, 5);
q = creat_Prime(5, 10);
/*
printf("请输入p：");
scanf("%d", &p);
printf("请输入q：");
scanf("%d", &q);
*/
//求n和z
n = q * p;
z = (p - 1) * (q - 1);
//随机生成e：e和z互素，e < n
do
{
e = creat_Prime(1, n);
} while (gcd(e, z) != 1);
/*
printf("请输入e：");
scanf("%d", &e);
*/
//求d：d是e的逆元，mod z
d = reverse(e, z);
printf("p=%d\nq=%d\nn=%d\nz=%d\ne=%d\nd=%d\n", p,q,n,z,e,d);
//输出公私钥
printf("公钥为：{n,e}={%d,%d}\n", n, e);
printf("私钥为：{d}={%d}\n", d);
printf("\n\t 2、加密\n");
//明文生成\输入
printf("请输入明文m：");
scanf("%d",&m);
//加密
c = power(m,e,n);
printf("明文为：{m}={%d}\n", m);
printf("密文为：{c}={%d}\n", c);
printf("\n\t 3、解密\n");
//解密
m1 =power(c,d,n);
printf("解密后明文：{m1}={%d}\n\n", m1);
}
//乘法同态测试
void mult_test()
{
printf("\n------------RSA乘法同态------------\n");
printf("\n\t 1、密钥生成\n");
//p和q是大素数;n=pq;z=(p-1)(q-1);任取e，使满足gcd(e,z)=1;d是e的逆;m是明文;c是密文;m1是解密后明文
int p, q, n, z, e, d, m_1,m_2,c_1,c_2,m,c;
//随机生成p和q
p = creat_Prime(1, 5);
q = creat_Prime(5, 10);
/*
printf("请输入p：");
scanf("%d", &p);
printf("请输入q：");
scanf("%d", &q);
*/
//求n和z
n = q * p;
z = (p - 1) * (q - 1);
//随机生成e：e和z互素，e < n
do
{
e = creat_Prime(1, n);
} while (gcd(e, z) != 1);
/*
printf("请输入e：");
scanf("%d", &e);
*/
//求d：d是e的逆元，mod z
d = reverse(e, z);
printf("p=%d\nq=%d\nn=%d\nz=%d\ne=%d\nd=%d\n", p,q,n,z,e,d);
//输出公私钥
printf("公钥为：{n,e}={%d,%d}\n", n, e);
printf("私钥为：{d}={%d}\n", d);
printf("\n\t 2、加密\n");
//明文生成\输入
printf("请输入明文m1：");
scanf("%d",&m_1);
printf("请输入明文m2：");
scanf("%d",&m_2);
//加密
c_1 = power(m_1,e,n);
c_2 = power(m_2,e,n);
printf("明文为：{m_1}={%d},{m_2}={%d}\n", m_1,m_2);
printf("密文为：{c_1}={%d},{c_2}={%d}\n", c_1,c_2);
printf("\n\t 3、乘法同态\n");
//乘法同态
c=c_1*c_2%n;
printf("密文乘为：{c_1*c_2}={%d}\n",c);
printf("\n\t 4、解密\n");
//解密
m = power(c,d,n);
printf("解密后明文：{m_1*m_2}={%d}\n\n", m);
}
int main()
{
int choose;
printf("请输入序号：【1】加解密测试，【2】乘法同态性测试\n");
scanf("%d",&choose);
if(choose ==1)
{
//加解密测试
encrypt_test();
}else if(choose ==2)
{
//乘法同态性测试
mult_test();
}else
printf("请重新输入！");
system("pause");
return 0;
}
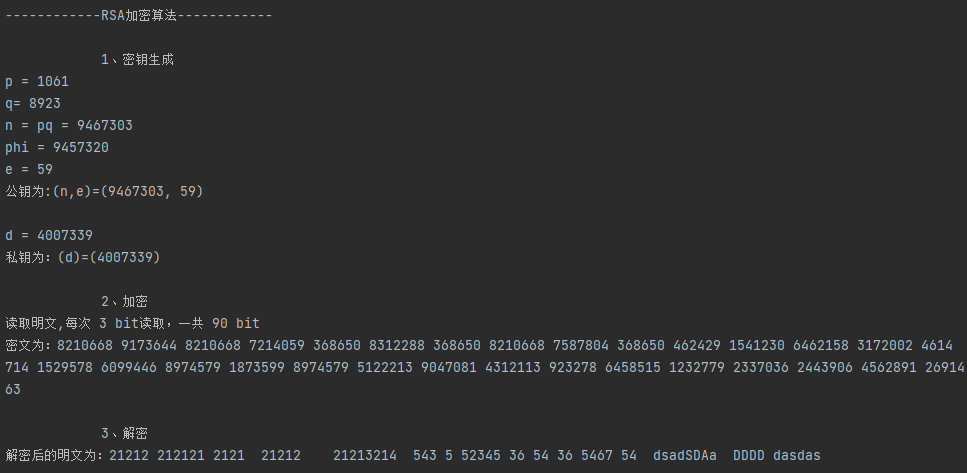
2、不使用miracl库实现大数计算，可加解密txt文件（数字和字母）+
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
#define ACCURACY 5
#define SINGLE_MAX 10000
#define EXPONENT_MAX 1000
#define BUF_SIZE 1024
/**
* 快速模幂：a^b mod c
*/
int modpow(long long a, long long b, int c) {
int res = 1;
while (b > 0) {
/* Need long multiplication else this will overflow... */
if (b & 1) {
res = (res * a) % c;
}
b = b >> 1;
a = (a * a) % c; /* Same deal here */
}
return res;
}
/**
* Computes the Jacobi symbol, (a, n)
*/
int jacobi(int a, int n) {
int twos, temp;
int mult = 1;
while (a > 1 && a != n) {
a = a % n;
if (a <= 1 || a == n) break;
twos = 0;
while (a % 2 == 0 && ++twos) a /= 2; /* Factor out multiples of 2 */
if (twos > 0 && twos % 2 == 1) mult *= (n % 8 == 1 || n % 8 == 7) * 2 - 1;
if (a <= 1 || a == n) break;
if (n % 4 != 1 && a % 4 != 1) mult *= -1; /* Coefficient for flipping */
temp = a;
a = n;
n = temp;
}
if (a == 0) return 0;
else if (a == 1) return mult;
else return 0; /* a == n => gcd(a, n) != 1 */
}
/**
* Check whether a is a Euler witness for n
*/
int solovayPrime(int a, int n) {
int x = jacobi(a, n);
if (x == -1) x = n - 1;
return x != 0 && modpow(a, (n - 1) / 2, n) == x;
}
/**
* 使用k的精度测试 n是否可能是素数（ Solovay-Strassen概率性素性检测法）
*/
int probablePrime(int n, int k) {
if (n == 2) return 1;
else if (n % 2 == 0 || n == 1) return 0;
while (k-- > 0) {
if (!solovayPrime(rand() % (n - 2) + 2, n)) return 0;
}
return 1;
}
/**
* 随机生成[3,n]之间的素数，分布趋于随机
*/
int randPrime(int n) {
int prime = rand() % n;
n += n % 2; /* n needs to be even so modulo wrapping preserves oddness */
prime += 1 - prime % 2;
while (1) {
if (probablePrime(prime, ACCURACY)) //4
return prime;
prime = (prime + 2) % n;
}
}
/**
* Compute gcd(a, b)
*/
int gcd(int a, int b) {
int temp;
while (b != 0) {
temp = b;
b = a % b;
a = temp;
}
return a;
}
/**
* 随机生成[3,n]之间的素数，且满足gcd(c,phi)=1，分布趋于随机
*/
int randExponent(int phi, int n) {
int e = rand() % n;
while (1) {
if (gcd(e, phi) == 1) return e;
e = (e + 1) % n;
if (e <= 2) e = 3;
}
}
/**
* Compute n^-1 mod m by 扩展欧几里得算法
*/
int inverse(int n, int modulus) {
int a = n, b = modulus;
int x = 0, y = 1, x0 = 1, y0 = 0, q, temp;
while (b != 0) {
q = a / b;
temp = a % b;
a = b;
b = temp;
temp = x; x = x0 - q * x; x0 = temp;
temp = y; y = y0 - q * y; y0 = temp;
}
if (x0 < 0) x0 += modulus;
return x0;
}
/**
* 将文件读入准备加密的字节数组。数组将用零填充，直到它除以每个块加密的字节数。返回读取的字节数。
*/
int readFile(FILE* fd, char** buffer, int bytes) {
int len = 0, cap = BUF_SIZE, r;
char buf[BUF_SIZE];
*buffer = (char*)malloc(BUF_SIZE * sizeof(char));
while ((r = fread(buf, sizeof(char), BUF_SIZE, fd)) > 0) {
if (len + r >= cap) {
cap *= 2;
*buffer = (char*)realloc(*buffer, cap);
}
memcpy(&(*buffer)[len], buf, r);
len += r;
}
/* 用零填充最后一个块，表示密码结束。如果没有空间，则添加一个附加块 */
if (len + bytes - len % bytes > cap) *buffer = (char*)realloc(*buffer, len + bytes - len % bytes);
do {
(*buffer)[len] = '\0';
len++;
} while (len % bytes != 0);
return len;
}
/**
* 加密, c = m^e mod n
*/
int encode(int m, int e, int n) {
return modpow(m, e, n);
}
/**
* 解密, m = c^d mod n
*/
int decode(int c, int d, int n) {
return modpow(c, d, n);
}
/**
* Encode the message of given length, using the public key (exponent, modulus)
* The resulting array will be of size len/bytes, each index being the encryption
* of "bytes" consecutive characters, given by m = (m1 + m2*128 + m3*128^2 + ..),
* encoded = m^exponent mod modulus
*/
int* encodeMessage(int len, int bytes, char* message, int exponent, int modulus) {
int* encoded = (int*)malloc((len / bytes) * sizeof(int));
int x, i, j;
for (i = 0; i < len; i += bytes) {
x = 0;
for (j = 0; j < bytes; j++)
x += message[i + j] * (1 << (7 * j));
encoded[i / bytes] = encode(x, exponent, modulus);
#ifndef MEASURE
printf("%d ", encoded[i / bytes]);
#endif
}
return encoded;
}
/**
* Decode the cryptogram of given length, using the private key (exponent, modulus)
* Each encrypted packet should represent "bytes" characters as per encodeMessage.
* The returned message will be of size len * bytes.
*/
int* decodeMessage(int len, int bytes, int* cryptogram, int exponent, int modulus) {
int* decoded = (int*)malloc(len * bytes * sizeof(int));
int x, i, j;
for (i = 0; i < len; i++) {
x = decode(cryptogram[i], exponent, modulus);
for (j = 0; j < bytes; j++) {
decoded[i * bytes + j] = (x >> (7 * j)) % 128;
#ifndef MEASURE
if (decoded[i * bytes + j] != '\0')
printf("%c", decoded[i * bytes + j]);
#endif
}
}
return decoded;
}
/**
* RSA算法加解密 text.txt 文件
*/
int main(void) {
int p, q, n, phi, e, d, bytes, len;
int* encoded, * decoded;
char* buffer;
FILE* f;
char str[600];
srand(time(NULL));
printf("\n------------RSA加密算法------------\n");
printf("\n\t 1、密钥生成\n");
while (1) {
p = randPrime(SINGLE_MAX);//10000
printf("p = %d\n", p);
q = randPrime(SINGLE_MAX);
printf("q= %d\n", q);
n = p * q;
printf("n = pq = %d\n", n);
if (n < 128) {
printf("模数小于128,无法编码单个字节,再试一次\n");
}
else
break;
}
if (n >> 21)
bytes = 3;
else if (n >> 14)
bytes = 2;
else
bytes = 1;
phi = (p - 1) * (q - 1);
printf("phi = %d\n", phi);
e = randExponent(phi, EXPONENT_MAX);
printf("e = %d\n公钥为:(n,e)=(%d, %d)\n\n", e, n, e);
d = inverse(e, phi);
printf("d = %d\n私钥为：(d)=(%d)", d,d);
printf("\n\n\t 2、加密\n");
printf("读取明文,");
f = fopen("text.txt", "r");
if (f == NULL) {
printf("打开文件失败！是否存在?\n");
return EXIT_FAILURE;
}
len = readFile(f, &buffer, bytes); /* len will be a multiple of bytes, to send whole chunks */
fclose(f);
printf("每次 %d bit读取，一共 %d bit\n密文为：",bytes,len);
encoded = encodeMessage(len, bytes, buffer, e, n);
printf("\n\n\t 3、解密\n解密后的明文为：");
decoded = decodeMessage(len / bytes, bytes, encoded, d, n);
printf("\n\n");
free(encoded);
free(decoded);
free(buffer);
system("pause");
return EXIT_SUCCESS;
}
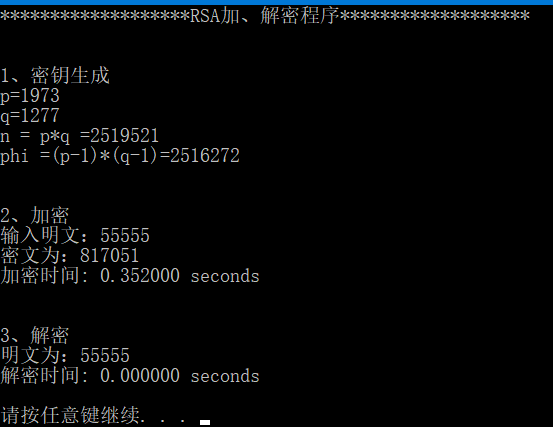
3、使用大数库miracl，加密1000次
#define _CRT_SECURE_NO_WARNINGS
#include "miracl.h"
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#pragma comment(lib,"miracl.lib")
//char *primetext="155315526351482395991155996351231807220169644828378937433223838972232518351958838087073321845624756550146945246003790108045940383194773439496051917019892370102341378990113959561895891019716873290512815434724157588460613638202017020672756091067223336194394910765309830876066246480156617492164140095427773547319";
char* text = "";
time_t begin, end;
int main()
{
/*
加解密
*/
big a, b, p, q, n, p1, q1, phi, pa, pb, key, e, d, dp, dq, t, m, c;
big primes[2], pm[2];
big_chinese ch;
long l = 12;
long cum = 0;
miracl* mip;
char input[256];
#ifndef MR_NOFULLWIDTH
mip = mirsys(100, 0);
#else
mip = mirsys(100, MAXBASE);
#endif
a = mirvar(0);
b = mirvar(0);
p = mirvar(0);
q = mirvar(0);
n = mirvar(0);
p1 = mirvar(0);
q1 = mirvar(0);
phi = mirvar(0);
pa = mirvar(0);
pb = mirvar(0);
e = mirvar(0);
d = mirvar(0);
dp = mirvar(0);
dq = mirvar(0);
t = mirvar(0);
m = mirvar(0);
c = mirvar(0);
pm[0] = mirvar(0);
pm[1] = mirvar(0);
printf("*******************RSA加、解密程序*******************\n\n");
printf("\n1、密钥生成\n");
do
{
bigbits(l, p);
if (subdivisible(p, 2)) incr(p, 1, p);
while (!isprime(p)) incr(p, 2, p);
bigbits(l, q);
if (subdivisible(q, 2)) incr(q, 1, q);
while (!isprime(q)) incr(q, 2, q);
multiply(p, q, n); /* n=p.q */
lgconv(65537L, e);
decr(p, 1, p1);
decr(q, 1, q1);
multiply(p1, q1, phi); /* phi =(p-1)*(q-1) */
} while (xgcd(e, phi, d, d, t) != 1);
printf("p=");
cotnum(p, stdout);
printf("q=");
cotnum(q, stdout);
printf("n = p*q =");
cotnum(n, stdout);
printf("phi =(p-1)*(q-1)=");
cotnum(phi, stdout);
/* set up for chinese remainder thereom */
primes[0] = p;
primes[1] = q;
crt_init(&ch, 2, primes);
copy(d, dp);
copy(d, dq);
divide(dp, p1, p1); /* dp=d mod p-1 */
divide(dq, q1, q1); /* dq=d mod q-1 */
printf("\n\n2、加密\n");
printf("输入明文：");
scanf("%s", input);
text = input;
mip->IOBASE = l;
cinstr(m, text);
mip->IOBASE = 10;
begin = clock();
while (cum < 10000)
{
powmod(m, e, n, c);
cum++;
}
printf("密文为：");
cotnum(c, stdout);
end = clock();
printf("加密时间: %f seconds\n", (double)(end - begin) / CLOCKS_PER_SEC);
zero(m);
printf("\n\n3、解密\n");
begin = clock();
powmod(c, dp, p, pm[0]); /* get result mod p */
powmod(c, dq, q, pm[1]); /* get result mod q */
crt(&ch, pm, m); /* combine them using CRT */
printf("明文为：");
mip->IOBASE = l;
cotnum(m, stdout);
crt_end(&ch);
end = clock();
printf("解密时间: %f seconds\n\n", (double)(end - begin) / CLOCKS_PER_SEC);
system("pause");
return 0;
}
签名方案
利用RSA构造签名方案，与加密方案类似，不同之处就是用私钥签名，用公钥验签。
原始方案
（1）密钥生成（Bob）
- 选取两个大素数\(p\)和\(q\)
- 计算\(n=p*q\),\(z=(p-1)(q-1)\)
- 任取一个正整数\(e\)，满足\(e<n\)和\(gcd(e,z)=1\)
- 取\(d\)，使其满足\(ed mod z=1\)
- 得到公钥\((n,e)\)，私钥\((d)\)
（2）签名（Alice）
- 消息\(m\in Z_n\)，对其签名\(s=m^d(mod n)\)，得到签名\(s\)
（3）验签（Bob）
- 对签名进行验证\(m=s^e(mod n)\)，若等式成立，则验证成功
（4）正确性
由于\(d*e=1 mod z\)，则\(s^e(mod n)=m^{d*e}(mod n)=m(mod n)\)
（5）问题
- 签名可以被伪造
比如Alice的消息\(x_1,x_2\)对应的签名是\(y_1,y_2\)，则敌手窃取到\(y_1,y_2\)，再由\(x_1=y_1^e(mod n),x_2=y_2^e(mod n)\)得到\(x_1,x_2\)，再重新自己签名发送给Bob，即伪造了签名
- 签名速度慢
由于带签名的消息是\(x\in Z_n\)，所以每次只能对\(\left \lfloor log_2n \right \rfloor\)位长的消息签名
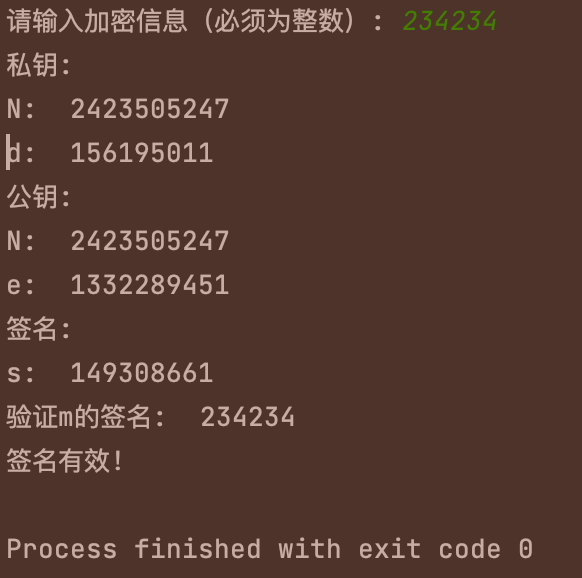
（6）程序实现
import random
import math
# 快速幂取模
def power(a, b, n): # 计算a**b mod n
if b == 0:
return 1 # 如果b值为0则返回1
elif b % 2 == 0: # 如果二进制b最后一位为0
p = power(a, b / 2, n) # 递归实现
return (p * p) % n # 取模运算
else:
return (a * power(a, b - 1, n)) % n # 返回结果
# 欧几里得算法求最大公约数
def gcd(a, b):
if a < b:
return gcd(b, a) # 如果a小于b，交换两个数
elif a % b == 0:
return b # 如果a整除于b则返回b
else:
return gcd(b, a % b) # 递归实现欧几里得算法
# 确定是否是素数
def isPrime(num):
if (num < 2):
return False # 如果num的值小于2返回false
else:
i = 2
flag = True
while i < num: # 如果num能被i整除，说明num不是质数
if num % i == 0:
flag = False # 只要num不是质数，将flag的值修改为 False
i += 1
return flag # 最后返回flag的值
# 生成大素数函数
def randPrime(n):
Start = 10 ** (n - 1) # n的值为5，计算开始值10**4
End = (10 ** n) - 1 # 计算结束10**5-1
while True:
num = random.randint(Start, End) # 返回从start到end之间任意一个数表示大素数
if isPrime(num): # 判断是否是质数，如果是则生成
return num # 返回大素数的值num
# 扩展的欧几里得算法，即ab=1 (mod n), 得到a在模n下的乘法逆元b
def Extended_Eulid(a, n):
x1, x2, x3 = 1, 0, n
y1, y2, y3 = 0, 1, a
while y3 != 1 and y3 != 0 and y3 > 0:
Q = math.floor(x3 / y3)
t1, t2, t3 = x1 - Q * y1, x2 - Q * y2, x3 - Q * y3
x1, x2, x3 = y1, y2, y3
y1, y2, y3 = t1, t2, t3
if y3 == 0:
return 0
if y3 == 1:
if y2 > 0:
return y2
else:
return n + y2
# 生成公钥和私钥
def KeyGen(p, q): # 分别计算n，e，d的值
n = p * q
e = random.randint(1, (p - 1) * (q - 1))
while gcd(e, (p - 1) * (q - 1)) != 1: # 运用欧几里得算法判断
e = random.randint(1, (p - 1) * (q - 1))
d = Extended_Eulid(e, (p - 1) * (q - 1))
return n, e, d
# 利用快速幂取模计算签名
def Sign(x, d, n):
s = power(x, d, n)
return s
# 利用快速幂取模判断是否有效签名
def Verify(s, e, n):
x_ = power(s, e, n)
return x_
# 主函数
if __name__ == '__main__':
key_size = 5
p = randPrime(key_size) # p与q分别为随机生成的大素数
q = randPrime(key_size)
n, e, d = KeyGen(p, q) # 用p与q生成公钥和私钥
# 输入消息
x = int(input("请输入加密信息（必须为整数）: "))
# 计算签名
s = Sign(x, d, n)
# 验证签名
x_ = Verify(s, e, n)
Valid = (x_ == x)
# 输出
print("私钥: ")
print("N: ", n)
print("d: ", d)
print("公钥: ")
print("N: ", n)
print("e: ", e)
print("签名: ")
print("s: ", s)
print("验证m的签名: ",x_)
if Valid:
print("签名有效!")
else:
print("签名无效!")
优化方案
解决办法就是加入Hash函数
（1）密钥生成（Bob）
- 选取两个大素数\(p\)和\(q\)
- 计算\(n=p*q\),\(z=(p-1)(q-1)\)
- 任取一个正整数\(e\)，满足\(e<n\)和\(gcd(e,z)=1\)
- 取\(d\)，使其满足\(ed mod z=1\)
- 得到公钥\((n,e)\)，私钥\((d)\)
（2）签名（Alice）
- 消息\(m\in Z_n\)，使用哈希算法（比如SHA512）生成摘要\(h\)，再用私钥对其签名\(s=h^d(mod n)\)，得到签名\(s\)
（3）验签（Bob）
- 使用哈希算法（比如SHA512）对消息\(m\)生成消息摘要\(h'\)，再用公钥对其验签\(h=c^e(mod n)\)
- 比较\(h\)和\(h'\)，若等式相同，则验证成功
（4）程序实现
# -*-coding:utf-8-*-
"""
File Name: RSA签名.py
Program IDE: PyCharm
Create Time: 2021-10-31 14:20
Create By Author: 陆依依
"""
import hashlib # 实现哈希
import random
# 产生大素数（w位）
def generate_prime(w):
while True:
# 产生一个奇数（）
num = random.randint(2 ** (w - 1), 2 ** w - 1) | 1
# 对素数进行50次素性检验, 错误概率为：7.888609052210118e-31， 可以忽略
for i in range(50):
if not Miller_Rabin(num):
break
if i == 49:
return num
# Miller-Rabin素性检测
def Miller_Rabin(num):
m = num - 1
k = 0
while m % 2 == 0:
m = m // 2
k = k + 1
a = random.randint(2, num)
b = Mod_P(a, m, num)
if b == 1:
return True
for i in range(k):
if b == num - 1:
return True
else:
b = b * b % num
return False
# 非递归求a^n mod p， 快速幂思想
def Mod_P(a, n, p):
c = 1
binstr = bin(n)[2:][::-1] # 通过切片去掉开头的0b，截取后面，然后反转
for item in binstr:
if item == '1':
c = (c * a) % p
a = (a ** 2) % p
elif item == '0':
a = (a ** 2) % p
return c
# 求最大公因子.欧几里得算法
def gcd(a, b):
if a % b == 0:
return b
else:
return gcd(b, a % b)
# 求逆元，扩展欧几里得算法
def Ex_Euclid(x, n):
r0 = n
r1 = x % n
if r1 == 1:
y = 1
else:
s0 = 1
s1 = 0
t0 = 0
t1 = 1
while r0 % r1 != 0:
q = r0 // r1
r = r0 % r1
r0 = r1
r1 = r
s = s0 - q * s1
s0 = s1
s1 = s
t = t0 - q * t1
t0 = t1
t1 = t
if r == 1:
y = (t + n) % n
return y
# 产生公私钥
def Build_key():
p = generate_prime(512)
q = generate_prime(512)
n = p * q # n的长度近似为1024位，即秘钥长度1024
_n = (p - 1) * (q - 1) # n的欧拉函数
while True:
e = random.randint(2, _n-1) # 随机选择一个与_n互质的整数，一般选择65537。
if gcd(e, _n) == 1: # 模拟计算
break
d = Ex_Euclid(e, _n) # 计算e对_n的模反元素
return n, e, d # 返回公私钥，公钥（n,e）,私钥（n,d）
def sign(m, n, d):
s = [Mod_P(ord(i), d, n) for i in m]
return m, s
def verify(m, s, n, e):
return m == ''.join([chr(Mod_P(i, e, n)) for i in s])
# demo
if __name__ == '__main__':
choose = int(input('请选择加密对象：1）文件 2）非文件\t'))
if choose == 2:
message = input('请输入待加密内容：').encode('utf-8')
else:
path = input('请输入完整文件路径：')
with open(path, 'rb') as f:
message = f.read()
m = hashlib.sha512(message).hexdigest()
print('散列后的消息：', m)
n, e, d = Build_key()
m, s = sign(m, n, d)
print('签名列表长度：', len(s))
# 将签名写入新文件
with open('sign.txt', 'w') as f:
f.write(str(s).replace('[', '').replace(']', '').replace(',', '\n').replace(' ', ''))
print('签名写入成功！！！')
print('签名验证结果？', verify(m, s, n, e))
ElGamal
1985年提出ElGamal公钥密码体制， 基于的是离散对数问题（或者说是难解的循环群），主要为数字签名而设计，缺点是密文比明文长，通常是密文长度的两倍。
ElGamal既可以在有限域上也可以在椭圆曲线上构成的循环群中计算。
椭圆曲线密码体制相比于基于有限域的密码体制有以下优点：
（1）安全性高
（2）密钥量小
（3）灵活性高
有限域加密方案
密钥生成
设\(G\)是有限域\(Z_p^*\)上的乘法循环群，\(p\)是一个素数，\(g\)是\(Z_p^*\)的生成元（\(Z_p^*\)和\(g\)是公开的）
随机选取一个整数\(a\in (1,p-1)\)，计算\(b=g^a(mod p)\)
则私钥为\((a)\)，公钥为\((p,g,b)\)
加密
对于明文消息\(m\)，随机选择一个整数\(k\in (1,p-1)\)，计算\(r=g^k(mod p)\)和\(v=m*b^k(mod p)\)，得到密文\(c=(r,v)\)
解密
计算\(\frac{v}{r^a}=\frac{m*b^k}{g^{k*a}}(mod p))=m(mod p)\)
乘法同态
给定两个密文\(c_1=(r1,v1),c_2=(r2,v2)\)：
\(D(c_1*c_2)=D(r1*r2,v1*v2)=D(g^{k_1+k_2}(mod p),m_1*m_2*b^{k_1+k_2}(mod p)) =\\\frac{m_1*m_2*b^{k_1+k_2}}{g^{a*(k_1+k_2})}(mod p)=m_1*m_2(mod p)\)
正确性
因为\(b=g^a(mod p)\)，则\(\frac{v}{r^a}=\frac{m*b^k}{g^{k*a}}(mod p))=\frac{m*g^{a*k}}{g^{k*a}}(mod p))=m(mod p)\)
安全性
体现在公钥生成中，即根据公钥\((p,g,b)\)不能恢复出私钥\((a)\)
由于\(b=g^a(mod p)\)，根据离散对数问题，已知\(p,b,g\)，难以求出\(a\)。
下面给出一个例子：
程序实现
/*
* ElGamal算法实现
* 功能：加解密、乘法同态
*/
#include<iostream>
#include<cstdio>
#define randomInt(a,b) (rand()%(b-a)+a) //生成指定范围的随机数
using namespace std;
typedef long long ll;
typedef struct C{
ll c_1;
ll c_2;
};
ll p,a,x,y,r,m1,m2;
C c1,c2,c3;
ll qpow(ll r, ll n, ll mod){//计算a^n % mod
ll re = 1;
while(n){
if(n & 1)
re = (re * r) % mod;
n >>= 1;
r = (r * r) % mod;
}
return re % mod;
}
ll byy(ll lp){//求Zlp*的生成元
bool flag;
for(ll i=2;i<lp;i++){
flag=true;
for(ll j=2;j<lp-1;j++){
if((lp-1)%j==0){
if(qpow(i,j,lp)==1) flag=false;
}
}
if(flag) return i;
}
}
ll inv(ll la, ll lp){//求逆元——扩展欧几里得算法
if(la == 1) return 1;
return inv(lp%la,lp)*(lp-lp/la)%lp;
}
C encode(ll la,ll lp,ll ly,ll lm){
C c;
printf("\n======加密======\n");
ll lr=randomInt(1,lp-1);
printf("随机数r=%lld\n",lr);
c.c_1=qpow(la,lr,lp);
c.c_2=(lm*qpow(ly,lr,lp))%lp;
printf("得到的密文为c_1=%lld c_2=%lld\n",c.c_1,c.c_2);
return c;
}
void decode(ll lx,ll lp,C c){
printf("\n======解密======\n");
c.c_1=qpow(c.c_1,lx,lp);
c.c_1=inv(c.c_1,lp);
ll m=(c.c_1*c.c_2)%lp;
printf("得到的明文为m=%lld\n",m);
}
C mult_c(ll lp,C lc1,C lc2){ //同态乘法
C c;
printf("\n======同态乘法======\n");
c.c_1=(lc1.c_1*lc2.c_1)%lp;
c.c_2=(lc1.c_2*lc2.c_2)%lp;
printf("密文相乘后c_1=%lld c_2=%lld\n",c.c_1,c.c_2);
return c;
}
int main(){
printf("请输入参数p:");
scanf("%lld",&p);
a=byy(p);
printf("计算出本原元a=%lld \n",a);
printf("\n======密钥生成======\n");
x=randomInt(1,p-1);
y=qpow(a,x,p);
printf("公钥pk={%lld,%lld,%lld}，私钥sk={%lld}\n",p,a,y,x);
printf("测试加解密，输入1；测试乘法同态，输入2\n");
int choose;
scanf("%d",&choose);
if(choose==1)
{
printf("请输入要加密的明文m：");
scanf("%lld",&m1);
c1=encode(a,p,y,m1); //加密
decode(x,p,c1); //解密
}else if(choose==2)
{
printf("请输入要加密的明文m1和m2：");
scanf("%lld%lld",&m1,&m2);
c1=encode(a,p,y,m1); //加密m1
c2=encode(a,p,y,m2); //加密m2
c3= mult_c(p,c1,c2);
decode(x,p,c3); //解密c3
printf("验证结果m1*m2=%lld\n",m1*m2%p);
}else
printf("选择错误，请重新选择！\n");
return 0;
}
椭圆曲线加密方案
密钥生成
选取一条椭圆曲线，得到群\(E_p(a,b)\)，取\(G\)为\(E_p(a,b)\)的生成元
选取整数\(n_A\)作为私钥，计算出\(P_A=n_AG\)作为公钥
加密
对于明文消息\(m\)，先将其嵌入到曲线上的点\(P_m\)，选取一个随机正整数\(k\)，计算出密文：
\(C_m=\left \{kG,P_m+kP_A \right \}\)
解密
使密文点对中的第二点减去私钥与第一个点的倍乘，即\(P_m+kP_A-n_AkG=P_m\)
加法同态
给定两个密文\(C_{m_1},C_{m_2}\)，有：
\(D(C_{m_1}+C_{m_2})=D((k_1+k_2)G,(P_{m_1}+P_{m_2})+(k_1+k_2)P_A)=\\(P_{m_1}+P_{m_2})+(k_1+k_2)P_A-n_A((k_1+k_2)G)=P_{m_1}+P_{m_2}\)
正确性
由于\(P_A=n_AG\)，则\(P_m+kP_A-n_AkG=P_m+kn_AG-n_AkG=P_m\)
安全性
椭圆曲线上的点构成了Abel群\(E_p(a,b)\)，在密钥生成阶段，给出公钥\(P_A=n_AG\)，难以求出私钥\(n_A\)，这就是椭圆曲线上的离散对数问题。
程序实现
实现重点：椭圆曲线上的计算（倍乘、累加）
#include "ElGamal.h"
//代码：https://github.com/ProbeTS/Cryptography/tree/master/ELGama
int main() {
int p=751,a=-1,b=188;
ELGama* e = new ELGama(p, a, b);
//生成元
Point G={0,376};
//密钥
int n_A=58; //私钥
Point P_A=e->kPcal(G, n_A); //公钥
//加密
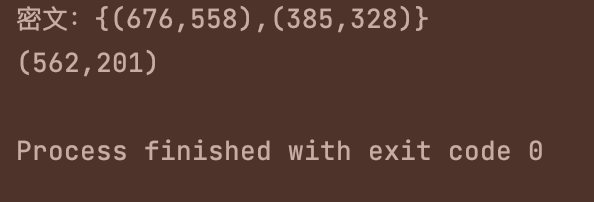
Point P_m={562,201};
int k=386;
Point c1=e->kPcal(G, k);
Point c2=e->PplusQcal(P_m,e->kPcal(P_A, k));
cout <<"密文：{("<<c1.x<<","<<c1.y<<"),("<<c2.x<<","<<c2.y<<")}"<< endl;
//解密
Point M=e->PplusQcal(c2, add_Reverse(e->kPcal(c1,n_A)));
cout <<"("<<M.x<<","<<M.y<<")"<< endl;
return 0;
}
EC-ElGamal加密方案（铜锁）
来自：https://blog.csdn.net/SOFAStack/article/details/123366669
密钥生成
选取一条椭圆曲线，得到群\(E_p(a,b)\)，取\(G\)为\(E_p(a,b)\)的生成元
随机选取整数\(n_A\in(1,p)\)作为私钥，计算出\(P_A=n_AG\)作为公钥
加密
对于明文消息\(m\)，选取一个随机正整数\(k\)，计算出密文：$C_m=E(m,k)=(kG,mG+kP_A) $
这里要求\(m\)取值很小，否则椭圆曲线的离散对数问题（ECDLP）无法求解，因为这里解密是需要查表的
解密
（1）先计算\(n_AC_m[0]=n_AkG=kP_A\)
（2）再计算\(C_m[1]-kP_A=mG+kP_A-kP_A=mG\)
（3）通过查表的方式，求解ECDLP问题，进而获得\(m\)
同态性
（1）加法
对于两个密文$C_{m_1}=(k_1G,m_1G+k_1P_A) ,C_{m_2}=(k_2G,m_2G+k_2P_A) $，有：
\(C_{m_1}+C_{m_2}=((k_1+k_2)G,(m_1+m_2)G+(k_1+k_2)P_A)=E((m_1+m_2),k_1+k_2)\)
（2）减法
对于两个密文\(C_{m_1}=(k_1G,m_1G+k_1P_A) ,C_{m_2}=(k_2G,m_2G+k_2P_A)\)，有：
\(C_{m_1}-C_{m_2}=((k_1-k_2)G,(m_1-m_2)G+(k_1-k_2)P_A)=E((m_1-m_2),k_1-k_2)\)
（3）标量乘
对于密文\(C_{m_1}=(k_1G,m_1G+k_1P_A)\)，一个明文\(m_2\)有：
\(m_2C_{m_1}=(m_2k_1G,m_2m_1G+m_2k_1P_A)=E((m_1m_2),k_1m_2)\)
程序实现
//参考：https://blog.csdn.net/SOFAStack/article/details/123366669 https://tongsuo.readthedocs.io/zh/latest/Tutorial/PHE/ec-elgamal-sample/
#include <stdio.h>
#include <time.h>
#include <openssl/ec.h>
#include <openssl/pem.h>
#define CLOCKS_PER_MSEC (CLOCKS_PER_SEC/1000)
int main(int argc, char *argv[])
{
int ret = -1;
uint32_t r;
//密钥生成
clock_t begin, end;
EC_KEY *sk_eckey = NULL, *pk_eckey = NULL;
EC_ELGAMAL_CTX *ctx1 = NULL, *ctx2 = NULL;
EC_ELGAMAL_CIPHERTEXT *c1 = NULL, *c2 = NULL, *c3 = NULL;
EC_ELGAMAL_DECRYPT_TABLE *table = NULL;
FILE *pk_file = fopen("ec-pk.pem", "rb");
FILE *sk_file = fopen("ec-sk.pem", "rb");
if ((pk_eckey = PEM_read_EC_PUBKEY(pk_file, NULL, NULL, NULL)) == NULL)
goto err;
if ((sk_eckey = PEM_read_ECPrivateKey(sk_file, NULL, NULL, NULL)) == NULL)
goto err;
if ((ctx1 = EC_ELGAMAL_CTX_new(pk_eckey)) == NULL)
goto err;
if ((ctx2 = EC_ELGAMAL_CTX_new(sk_eckey)) == NULL)
goto err;
//创建解密表
begin = clock();
if ((table = EC_ELGAMAL_DECRYPT_TABLE_new(ctx2, 0)) == NULL)
goto err;
EC_ELGAMAL_CTX_set_decrypt_table(ctx2, table);
end = clock();
printf("EC_ELGAMAL_DECRYPT_TABLE_new(1) cost: %lfms\n", (double)(end - begin)/CLOCKS_PER_MSEC);
if ((c1 = EC_ELGAMAL_CIPHERTEXT_new(ctx1)) == NULL)
goto err;
if ((c2 = EC_ELGAMAL_CIPHERTEXT_new(ctx1)) == NULL)
goto err;
//加密20000021
begin = clock();
if (!EC_ELGAMAL_encrypt(ctx1, c1, 20000021))
goto err;
end = clock();
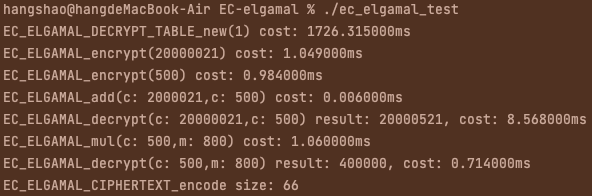
printf("EC_ELGAMAL_encrypt(20000021) cost: %lfms\n", (double)(end - begin)/CLOCKS_PER_MSEC);
//加密500
begin = clock();
if (!EC_ELGAMAL_encrypt(ctx1, c2, 500))
goto err;
end = clock();
printf("EC_ELGAMAL_encrypt(500) cost: %lfms\n", (double)(end - begin)/CLOCKS_PER_MSEC);
if ((c3 = EC_ELGAMAL_CIPHERTEXT_new(ctx1)) == NULL)
goto err;
//密文相加：20000021+500
begin = clock();
if (!EC_ELGAMAL_add(ctx1, c3, c1, c2))
goto err;
end = clock();
printf("EC_ELGAMAL_add(c: 2000021,c: 500) cost: %lfms\n", (double)(end - begin)/CLOCKS_PER_MSEC);
//解密：20000021+500
begin = clock();
if (!(EC_ELGAMAL_decrypt(ctx2, &r, c3)))
goto err;
end = clock();
printf("EC_ELGAMAL_decrypt(c: 20000021,c: 500) result: %d, cost: %lfms\n", r, (double)(end - begin)/CLOCKS_PER_MSEC);
//标量乘：500*800
begin = clock();
if (!EC_ELGAMAL_mul(ctx1, c3, c2, 800))
goto err;
end = clock();
printf("EC_ELGAMAL_mul(c: 500,m: 800) cost: %lfms\n", (double)(end - begin)/CLOCKS_PER_MSEC);
//解密：500*800
begin = clock();
if (!(EC_ELGAMAL_decrypt(ctx2, &r, c3)))
goto err;
end = clock();
printf("EC_ELGAMAL_decrypt(c: 500,m: 800) result: %d, cost: %lfms\n", r, (double)(end - begin)/CLOCKS_PER_MSEC);
//将密文500*800编码为二进制文件
printf("EC_ELGAMAL_CIPHERTEXT_encode size: %zu\n", EC_ELGAMAL_CIPHERTEXT_encode(ctx2, NULL, 0, NULL, 1));
ret = 0;
err:
EC_KEY_free(sk_eckey);
EC_KEY_free(pk_eckey);
EC_ELGAMAL_DECRYPT_TABLE_free(table);
EC_ELGAMAL_CIPHERTEXT_free(c1);
EC_ELGAMAL_CIPHERTEXT_free(c2);
EC_ELGAMAL_CIPHERTEXT_free(c3);
EC_ELGAMAL_CTX_free(ctx1);
EC_ELGAMAL_CTX_free(ctx2);
fclose(sk_file);
fclose(pk_file);
return ret;
}
阈值加密方案
签名方案
1985年提出基于离散对数的签名方案，1991年进行改进后，叫做DSS。
下面给出的是在有限域上的
密钥生成（Bob）
设\(G\)是有限域\(Z_p^*\)上的乘法循环群，\(p\)是一个素数，\(g\)是\(Z_p^*\)的生成元（\(Z_p^*\)和\(g\)是公开的）
随机选取一个整数\(a\in (1,p-1)\)，计算\(b=g^a(mod p)\)
则私钥为\((a)\)，公钥为\((p,g,b)\)
签名（Alice）
对于消息\(m\)，随机取整数\(k\in (1,p-1)\)，计算签名值：\(r=g^k(mod p),s=(h(m)-r*a)*k^{-1}mod (p-1)\)，其中\(h(.)\)是hash函数，将签名\((r,s)\)和消息\(m\)发送给Bob
验签（Bob）
先计算\(g^{h(m)}\)，然后计算\(b^r*r^s\)，判断两者是相等，若相等则验证成功。
正确性
由于\(s=(h(m)-r*a)*k^{-1}mod (p-1)\)，则\(s*k+a*r=(h(m)-r*a+r*a)mod (p-1)=h(m)mod (p-1)\)，所以\(g^{h(m)}=g^{s*k+a*r}=g^{s*k}*g^{a*r}=r^s*b^r(mod p)\)
程序实现
import random
# 求最大公约数
def gcd(a, b):
if a < b:
return gcd(b, a)
elif a % b == 0:
return b
else:
return gcd(b, a % b)
# 快速幂+取模
def power(a, b, c):
ans = 1
while b != 0:
if b & 1:
ans = (ans * a) % c
b >>= 1
a = (a * a) % c
return ans
# 卢卡斯-莱墨素性检验
def Lucas_Lehmer(num) -> bool: # 快速检验pow(2,m)-1是不是素数
if num == 2:
return True
if num % 2 == 0:
return False
s = 4
Mersenne = pow(2, num) - 1 # pow(2, num)-1是梅森数
for x in range(1, (num - 2) + 1): # num-2是循环次数，+1表示右区间开
s = ((s * s) - 2) % Mersenne
if s == 0:
return True
else:
return False
# 大素数检测
def Miller_Rabin(n):
a = random.randint(2,n-2) #随机第选取一个a∈[2,n-2]
# print("随机选取的a=%lld\n"%a)
s = 0 #s为d中的因子2的幂次数。
d = n - 1
while (d & 1) == 0: #将d中因子2全部提取出来。
s += 1
d >>= 1
x = power(a, d, n)
for i in range(s): #进行s次二次探测
newX = power(x, 2, n)
if newX == 1 and x != 1 and x != n - 1:
return False #用二次定理的逆否命题，此时n确定为合数。
x = newX
if x != 1: # 用费马小定理的逆否命题判断，此时x=a^(n-1) (mod n)，那么n确定为合数。
return False
return True # 用费马小定理的逆命题判断。能经受住考验至此的数，大概率为素数。
# 扩展的欧几里得算法，ab=1 (mod m), 得到a在模m下的乘法逆元b
def Extended_Eulid(a: int, m: int) -> int:
def extended_eulid(a: int, m: int):
if a == 0: # 边界条件
return 1, 0, m
else:
x, y, gcd = extended_eulid(m % a, a) # 递归
x, y = y, (x - (m // a) * y) # 递推关系，左端为上层
return x, y, gcd # 返回第一层的计算结果。
# 最终返回的y值即为b在模a下的乘法逆元
# 若y为复数，则y+a为相应的正数逆元
n = extended_eulid(a, m)
if n[1] < 0:
return n[1] + m
else:
return n[1]
# 生成域参数p，长度大约为512bits
def Generate_p() -> int:
a = random.randint(10**150, 10**160)
while gcd(a, 2) != 1:
a = random.randint(10**150, 10**160)
return a
# 生成域参数alpha
def Generate_alpha(p: int) -> int:
return random.randint(2, p)
# 生成一个小于p的素数作为私钥，长度大约为512bits
def Generate_private_key(p: int) -> int:
pri = random.randint(2, p - 2)
while gcd(pri, p) != 1:
pri = random.randint(2, p - 2)
return pri
# 快速幂
def quick_power(a: int, b: int) -> int:
ans = 1
while b != 0:
if b & 1:
ans = ans * a
b >>= 1
a = a * a
return ans
def Generate_prime(key_size: int) -> int:
while True:
num = random.randrange(quick_power(2, key_size - 1), quick_power(2, key_size))
if Miller_Rabin(num):
return num
# 计算签名
def Sign(x, p, alpha, d) -> []:
temp_key = random.randint(0, p - 2)
while gcd(temp_key, p - 1) != 1:
temp_key = random.randint(0, p - 2)
r = power(alpha, temp_key, p)
s = (x - d * r) * Extended_Eulid(temp_key, p - 1) % (p - 1)
return r, s
# 签名验证
def Verify(x, p, alpha, beta, r, s):
t = (power(beta, r, p) * power(r, s, p)) % p
if t == power(alpha, x, p):
return True
else:
return False
if __name__ == '__main__':
x = int(input("Message: "))
if type(x) != int:
raise ValueError("Must be an integer!")
p = Generate_prime(512)
alpha = Generate_alpha(p)
a = Generate_private_key(p)
beta = power(alpha, a, p)
r, s = Sign(x, p, alpha, a)
Valid = Verify(x, p, alpha, beta, r, s)
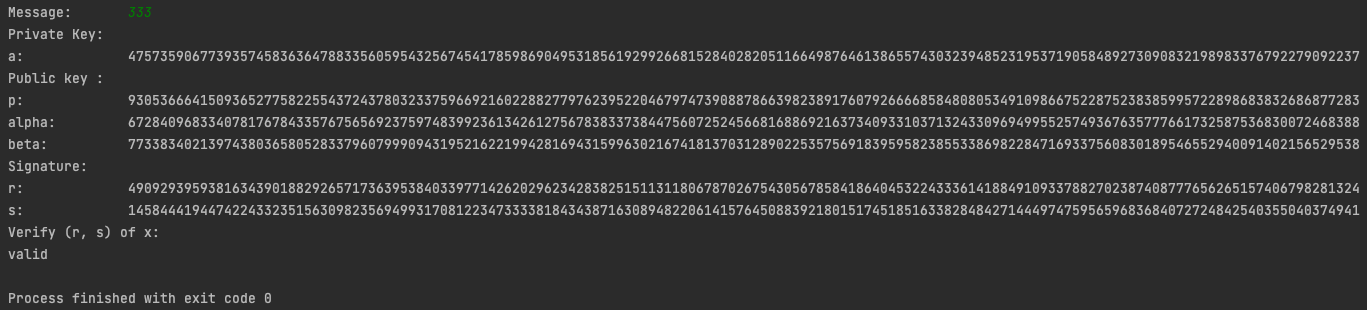
print("Private Key: ")
print("a: ", a)
print("Public key : ")
print("p: ", p)
print("alpha: ", alpha)
print("beta: ", beta)
print("Signature: ")
print("r: ", r)
print("s: ", s)
print("Verify (r, s) of x: ")
if Verify(x, p, alpha, beta, r, s):
print("valid")
else:
print("invalid")
Paillier
Paillier加密方案，最初于1999年首次提出，此后又进行优化，下面给出原版和优化后的方案，该方案因为效率高，安全性证明完备，又具有同态性质在隐私计算中广泛应用。
原方案：Public-key cryptosystems based on composite degree residuosity classes
优化方案：
原方案
密钥生成
- 随机选择两个大素数\(p,q\)，满足\(gcd(p*q,(p-1)*(q-1))=1\)，且\(p,q\)长度相等
- 计算出\(n=p*q\)和\(\lambda=lcm(p-1,q-1)\)，其中\(lcm()\)表示最小公倍数
- 随机选择一个整数\(g\in Z_{n^2}^*\)
- 定义\(L\)函数：\(L(x)=\frac{x-1}{n}\)，计算\(u=(L(g^{\lambda} mod n^2))^{-1}mod n\)
- 得到公钥：\((n,g)\)，私钥：\((\lambda,u)\)
加密
- 对于明文消息\(m\in [0,n]\)
- 选择一个随机数\(r\in [0,n]\)，且\(r\in Z_n^*\)
- 计算密文\(c=E(m,r)=g^m*r^nmod n^2\)
解密
- 对于密文消息\(c\in Z_{n^2}^*\)
- 计算出明文\(m=D(c)=L(c^{\lambda}mod n^2)*u (mod n)\)
同态性
（1）加法
对于两个密文\(c_1,c_2\)，有\(D((c_1*c_2)mod n^2)=D((g^{m_1}*r_1^n*g^{m_2}*r_2^n)mod n^2)=D((g^{m_1+m_2}*(r_1*r_2)^n)mod n^2)\)，即\(E(m_1+m_2,r_1*r_2)=c_1*c_2\)
对于密文\(c_1\)和明文\(m_2\)，有：
\(D(c_1*g^{m_2}mod n^2)=D((g^{m_1*m_2}*r^nmod n^2)=m_1+m_2\)，即\(E(m_1*m_2,r^{m_2})\)
（2）标量乘法
对于密文\(c_1\)和明文\(m_2\)，有：
\(D(c_1^{m_2}mod n^2)=D((g^{m_1*m_2}*(r^{m_2})^nmod n^2)=m_1*m_2\)，即\(E(m_1*m_2,r^{m_2})\)
正确性
\(D(c)=L(c^{\lambda}mod n^2)*u (mod n)=\frac{L((g^m*r^n)^{\lambda}(mod n^2)}{L(g^{\lambda} mod n^2)}=m\)
具体证明见：
安全性
Paillier加密基于的是复合剩余类问题，即给定合数\(n\)和整数\(z\)，难以确定\(z\)是否是模\(n^2\)的\(n\)次剩余，对于\(z=y^n(mod n^2)\)。
程序实现
（1）Python实现
#!/usr/bin/env python
from paillier.Paillier import *
# Press the green button in the gutter to run the script.
if __name__ == '__main__':
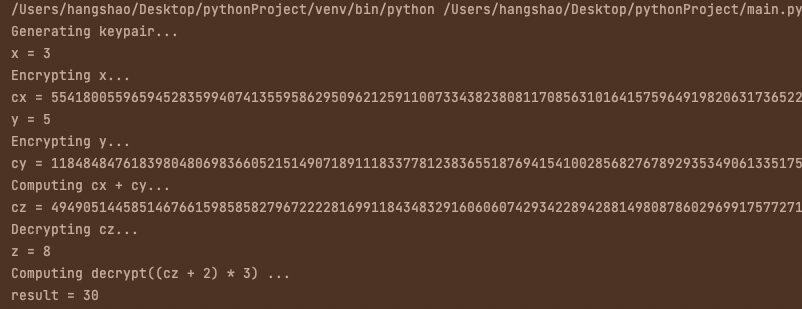
print("Generating keypair...")
priv, pub = generate_keypair(512)
x = 3
print("x =", x)
print("Encrypting x...")
cx = encrypt(pub, x)
print("cx =", cx)
y = 5
print("y =", y)
print("Encrypting y...")
cy = encrypt(pub, y)
print("cy =", cy)
print("Computing cx + cy...")
cz = e_add(pub, cx, cy)
print("cz =", cz)
print("Decrypting cz...")
z = decrypt(priv, pub, cz)
print("z =", z)
print("Computing decrypt((cz + 2) * 3) ...")
print("result =", decrypt(priv, pub, e_mul_const(pub, e_add_const(pub, cz, 2), 3)))
（2）C++实现（NTL库）
#include <iostream>
#include "paillier.h"
using namespace std;
using namespace NTL;
ZZ lcm(ZZ x, ZZ y){
ZZ ans = (x * y) / NTL::GCD(x,y);
return ans;
}
int main()
{
ZZ p = ZZ(43);
ZZ q = ZZ(41);
ZZ lambda = lcm(p - 1, q - 1);
Paillier paillier(p*q, lambda);
ZZ n = p * q;
cout << "p = " << p << endl;
cout << "q = " << q << endl;
cout << "n = " << n << endl;
//generator=lambda+1
cout << "lamdba = " << lambda << endl;
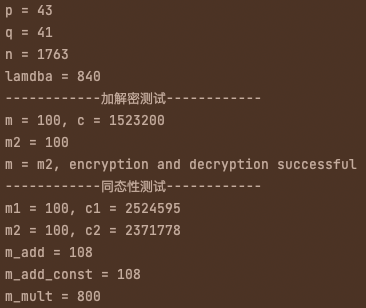
cout << "------------加解密测试------------"<<endl;
ZZ m = ZZ(100); //明文消息
ZZ c = paillier.encrypt(m);
cout << "m = "<<m<< ", c = " << c << endl;
ZZ m_ = paillier.decrypt(c);
cout << "m2 = " << m_ << endl;
if (m == m_){
cout << "m = m2, encryption and decryption successful" << endl;
}
cout << "------------同态性测试------------"<<endl;
ZZ m1 = ZZ(100); //明文消息
ZZ m2 = ZZ(8);
ZZ c1 = paillier.encrypt(m1, (ZZ)131 );
ZZ c2 = paillier.encrypt(m2, (ZZ)223 );
cout << "m1 = "<<m1<<", c1 = " << c1 << endl;
cout << "m2 = "<<m1<<", c2 = " << c2 << endl;
ZZ c_add=paillier.hom_add(c1,c2);
ZZ c_add_const=paillier.hom_add_const(c1,m2);
ZZ c_mult=paillier.hom_mult(c1,m2);
ZZ m_add = paillier.decrypt(c_add);
ZZ m_add_const = paillier.decrypt(c_add_const);
ZZ m_mult = paillier.decrypt(c_mult);
cout << "m_add = " << m_add << endl;
cout << "m_add_const = " << m_add_const << endl;
cout << "m_mult = " << m_mult << endl;
return 0;
}
优化方案
待补充
参考
1、现代密码学-杨波
2、密码学-基础理论与应用
