全同态加密研究：学习

学习李增鹏老师的文章：全同态加密研究，记录笔记。

摘要

• 云计算很重要，但存在“数据安全和隐私保护的问题”。
• 引出全同态加密，当前研究方向：（1）方案的设计和性能提升；（2）潜在应用。
• 本文内容：（1）介绍全同态发展的三个阶段（三类）；（2）方案设计和发展趋势；（3）近些年的研究成果。

引言

• 云计算存在问题：如何在保护数据安全和用户隐私的前提下完成安全计算。

• 同态加密：起源（隐私同态）、发展（部分同态）、全同态（Gentry09）、分类（Gentry09系列、基于RLWE的FHE系列、GSW系列）

FHE的定义

• 层次全同态加密（Leveled-FHE）支持有限次的同态计算，利用电路构造而成，包含四个功能（函数）：KeyGen、Enc、Dec、Eval（这里会的是计算密钥evk，是公开的）。

• 方案正确性：加解密正确性、计算正确性。

• \(C\in C_{\lambda}\)，其中\(C\)表示具体的计算函数，\(C_{\lambda}\)表示满足同态计算函数的集合。

• 紧致/紧凑性（Compactness）：密文大小（长度）与计算函数大小\(|C|\)、密文层数\(l\)无关。
• 安全性，定义的是IND-CPA安全，表示给定\(0\)和\(1\)的密文，无法在多想时间内区分出对应的明文，其中\(\lambda\)是安全参数。

FHE的研究现状

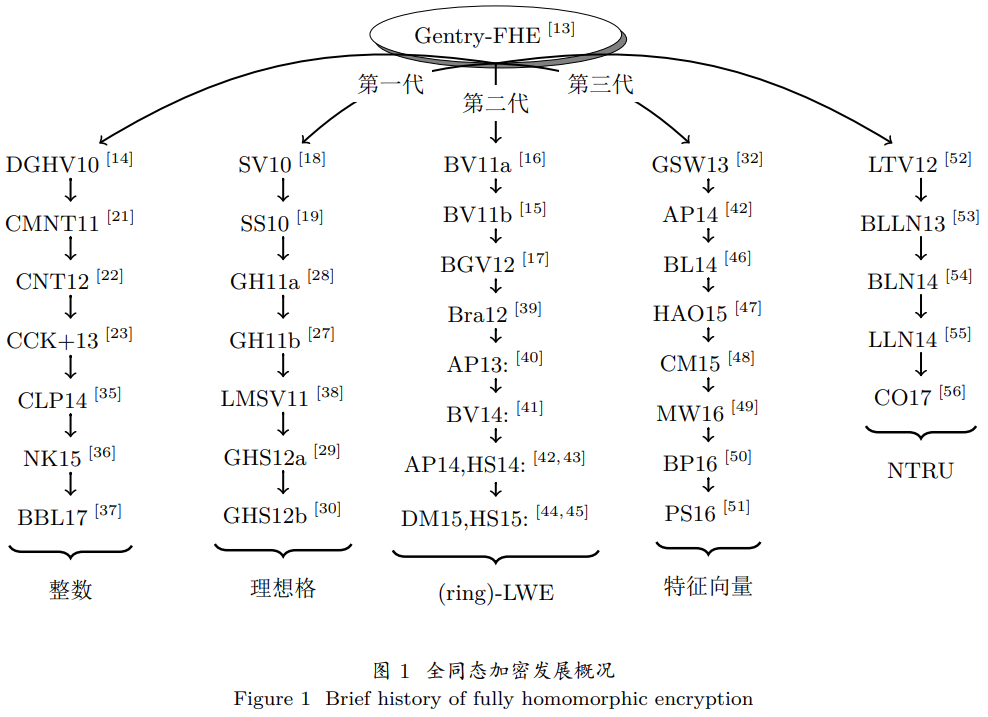
• 根据FHE基于的困难问题，即方案安全性的依据，可以分为：（1）格上的基于Regev的LWE问题；（2）整数上的AGCD问题。
• 基于格的构造，又可分为：（1）基于理想格的（Gentry09系列）；（2）基于LWE假设，利用密钥交换、模交换、重线性化等技术构造FHE（BV、BFV、BGV系列）；（3）基于LWE假设，利用近似特征向量而避免使用密钥交换等降维技术来构造FHE（GSW系列）；（4）基于NTRU，利用密钥交换等技术构造FHE。

基于格基的

基于理想格的（一代）

• Gentry09方案是在理想格上计算，依赖BDDP问题和SSSP问题。
• FHE设计方式：先设计一个SWHE或者Leveled-FHE，在通过自举（Bootstrapping）技术刷新密文，达到真正的FHE。
• 自举需要将私钥加密作为公共参数公开，所以无法抵抗CCA（CCA是敌手可以根据密文获得明文，这样就可以获取私钥了），只能达到CPA安全。
• 后续又有很多优化自举技术，但都依赖于SSSP假设，即假设（。。。），该假设目前并未被证明。
• 所以BV11出现了，不再依赖于SSSP假设，进入第二代FHE。

基于LWE的（二、三代）

• 第二代FHE是首次利用LWE假设实现的
• LWE问题是由Regev提出的，可以抵抗量子攻击，且实现简单。
• 随后出现基于RLWE设计的FHE，安全性量子规约到理想格上的困难问题，利用压缩范式（squashing）和自举（Bootstrapping）技术实现真正的FHE。
• 同年BV11-a提出，基于LWE假设，安全性依赖于格上的SVP问题，利用重线性化（Relinearization）实现层次FHE（SWHE或Leveled-FHE），进而利用Dimension-Modulus Reduction技术实现自举（Bootstrapping），不再使用压缩范式（squashing），这种方法能有效缩短密文、降低解密电路的复杂性（无需额外假设）。
• BGV12方案不依赖于自举实现层次FHE（SWHE或Leveled-FHE）
• Bra12方案利用张量积构造一个扩张因子不变的FHE，即模\(q\)与初始噪音\(B\)的比例保持不变，无需使用模交换（Modulus Switching）降噪。
• 第三代FHE，密文是矩阵，同态计算中密文的维数不会扩张，所以无需使用计算密钥(evk)来降维，经典的就是GSW方案，并在方案中首次实现基于身份的FHE和基于属性的FHE，当然方案只实现了Leveled-FHE，若想实现真正的FHE，还需使用自举。

基于整数的

• 基于整数上，指的就是DGHV系列，依赖AGCD假设。
• 最初是DGHV10方案，后续方案采用公钥压缩、模交换、批处理等技术优化，使其解密电路的复杂度降低。

总结

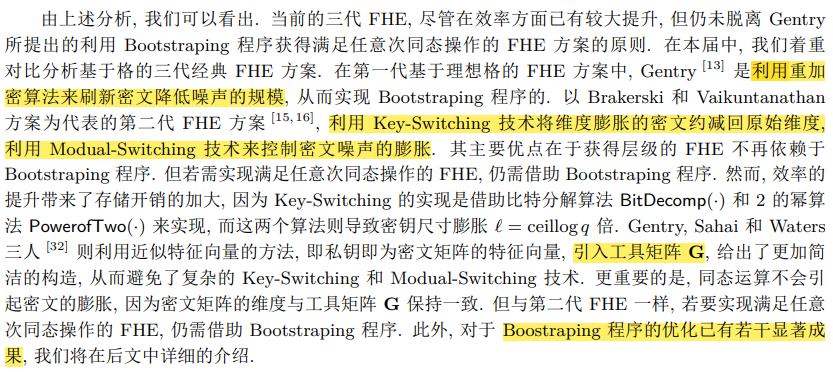
• 总的来说，目前要实现真正的FHE，惟一的方法还是自举。
• 第一代，实现真正FHE，即使用重加密刷新密文降低噪音，以此实现自举。
• 第二代，先使用密钥交换（重线性化）降维、模交换降噪实现Leveled-FHE，若想实现真正的FHE，还需要使用自举。
• 第三代，先使用比特分解（BitDecomp）和2的幂算法（PowerofTwo）及时实现Leveled-FHE，若想实现真正的FHE，还需要使用自举。

基于格的FHE

格公钥密码

• 格基规约算法是攻击公钥密码的常用工具之一，比如LLL算法。
• AD加密是第一个基于格上困难问题设计的加密方案。
• 当前格密码方案大都基于SIS问题和LWE问题设计，都可以规约到求解最坏情况的格困难问题。
• 规约越紧，参数选的越小，存储和计算效率高。
• 基于格上困难问题的公钥加密方案的优势：（1）格问题的计算复杂（格上任意随机实例的安全度都相同）；（2）格基密码计算高效（矩阵、向量间的乘法、线性求和、模运算等）；（3）格密码更安全（抗量子性）

LWE问题

• “一般情况下解决LWE问题并不比在最坏情况下解决一些格近似问题简单”，意思就是解决LWE问题同样困难。
• Regev证明了给出适合的参数，LWE问题和格上的SVP问题一样困难。

GSW方案

• 上面介绍的是GSW系列，并不是原方案。
• 密钥生成基于DLWE问题
• 加密时和原方案不同。
• 解密比较复杂：（1）选择合适的\(I\)，找到对应的\(C_I\)；（2）计算出\(x\)；（3）输出\(u'\)。
• 解密正确性：密文\(C\)是一个\((n+1)*N\)的矩阵，选择\(C_I\)是一个\(n+1\)维向量。

待补充。。。

问题和发展

性能

多比特加密

• 多比特就是批处理，对于单比特加密使用迭代或拼接等方式实现多比特，存在问题：密钥尺寸更长，计算开销大，加密噪音膨胀等。
• 针对第一代FHE，首次提出SIMD批处理技术；第二代，给出基于LWE的批处理FHE方案；第三代，构造既能实现批处理加密，也能实现一次性解密多比特的FHE方案。

计算效率

• FHE为什么慢？（1）自举，因为自举时，每个门电路都需要同态的调用解密电路；（2）密文膨胀，体现在密文维度膨胀和噪音膨胀，使用密钥交换或重线性化降维，使用模交换降噪，都会增加大量计算消耗。
• 自举（Bootstrapping）技术的发展？目前自举时间至少0.1s。

安全性

• 因为FHE具有同态属性，就有延展性，就不能达到CCA2安全。（适应性选择密文攻击是不限制敌手调用解密时间），目前大部分FHE只满足CPA安全。

• 就算满足CCA1安全，但方案不是紧凑的。

• 针对FHE的攻击：（1）密钥恢复攻击；（2）旁路攻击，所以提出抗泄漏的FHE方案。

应用

MPC

• FHE在MPC中的应用这里分为：门限FHE和多密钥FHE。
• 门限FHE，各方共享公钥，各自有一个私钥份，加密时各方使用相同公钥加密，解密时需要至少\(t\)份私钥才能正确解密。
• 多密钥FHE，各方拥有公私钥，加密时各方使用自己的公钥加密，不同公钥加密的密文可以执行同态计算，解密时先各自解密，最后聚合得到最终结果。

密文处理

• PIR和SE的区别：PIR是保护用户查询（重点是保护用户），SE是保护被查询文件（重点是保护数据）
• PIR、PSI、联合计算等应用

其他

• IBE、ABE、FE、WC、OPRF等都可以结合FHE

总结

• 基于格的FHE是大势。
• FHE的应用场景目前已经火了。
• FHE的广泛应用还需探究。
• FHE的效率研究还需多加努力。

内容量很大，学到很多，点赞~