安全多方计算之前世今生
系列学习&转载-绿盟的天枢实验室-关于MPC的文章
第一篇：“安全多方计算之前世今生”
安全多方计算简介
当前，数据被称为“新时代的石油”，数据只有流动（共享）起来才能产生更大的价值。各个国家已经深刻认识到了数据的重要性，并开始通过立法手段保护数据安全，各大机构/企业再希望像以前一样，粗暴的、毫无底线的收集和共享数据越来越困难。这就导致，如何在保证各机构/企业/个人数据私密性的前提下，实现多方数据的联合查询、统计与建模，成为了数据处理领域新的研究方向。
安全多方计算技术刚好能够满足上述需求。安全多方计算（Secure Multi-Party Computation，学术界简称MPC或SMPC，本系列文章统一简称为MPC）是一种通用的密码原语，它在不泄露参与方原始输入数据的前提下，允许分布式参与方合作计算任意函数，输出准确的计算结果，是目前国际密码学界的研究热点之一。
安全多方计算起源
安全多方计算问题起源于图灵奖获得者姚期智院士于1982年提出的百万富翁问题及其密码学解法[1]，后来经过不断的发展和完善，成为当前密码学的一个重要分支。
百万富翁问题
如图1所示，姚氏百万富翁问题可解释为：两个争强好胜的富翁Alice和Bob在街头相遇（假定Alice财富为\(x\)百万，Bob财富为\(y\)百万），如何在不暴露各自财富的前提下比较出谁更富有？
图1 姚氏百万富翁问题
百万富翁问题的通俗解法
对于图1中的姚氏百万富翁问题，我们以非密码学的、通俗易懂的语言解决该问题：
假定\(x=3\)，\(y=7\)，即Alice拥有3百万，Bob拥有7百万，他们只关心自己的财富在百万这个量级上，谁更富有。假定他们的财富都不会超过1千万，则可以默认为Alice和Bob的财富值\(x、y\)取值范围为1~9。
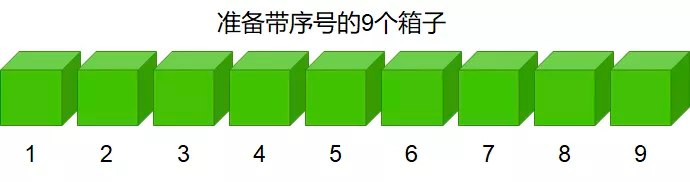
第一步：如图2所示，Alice首先准备带序号1-9的9个箱子。
图2 Alice首先准备带序号1-9的9个箱子
第二步：Alice在箱子内分别放入苹果和香蕉，规则为：如果箱子序号小于自己的财富值\(x\)，则放入苹果，否则放入香蕉。由于\(x=3\)，因此前2个箱子为苹果，后7个箱子为香蕉。
将带序号的9个箱子封装后，交给Bob。
图3 按序号和财富值在箱子内分别放入苹果和香蕉
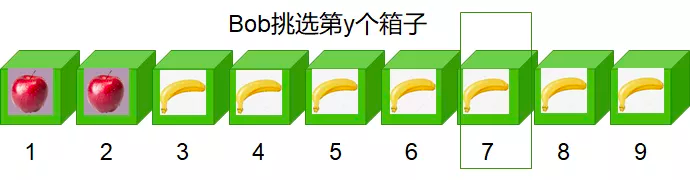
第三步：如图4所示，Bob收到带序号的箱子后，避开Alice的视线，挑选序号与自己财富值\(y\)相等的箱子，然后撕掉序号，扔掉其他箱子。注意，Bob只能诚实的挑选1次箱子。
图4 Bob收到9个箱子后的操作
第四步：Bob当着Alice的面打开选中的箱子，如果是香蕉，则\(y≥x\)；是苹果则\(x>y\)。本例中Alice最后看到的是一个如图5所示，没有序号的、带香蕉的箱子，表示\(x>y\)不成立，知道自己的财富不比Bob多。
图5 Alice最终看到的箱子
通过以上步骤可知，在最后阶段，虽然Alice和Bob都看到了箱子里放的是香蕉（MPC算法的计算结果），但由于箱子序号被撕掉，所以Alice并不知道Bob选的是第几个箱子（实现了Bob财富y对Alice的隐藏）；对于Bob来说，并不能确定序号1-6的6个箱子里，从第几个箱子开始，由苹果变成了香蕉（实现了Alice财富x对Bob的隐藏)。
百万富翁问题的密码学解法本文不再讲解，感兴趣的读者可阅读姚院士的原始文献（参考文献[1]），或阅读参考文献[2]中对姚院士论文的中文解读。
安全多方计算框架模型
安全多方计算可形式化描述为，n个计算参与方分别持有数据\(x_1,x_2,…,x_n\)，协议的目的是利用各方的秘密数据计算一个预先达成的共识函数\(y_1,y_2,...,y_n=f(x_1,x_2,…,x_n)\)，此时任意一方可以得到对应的结果\(yi\)，但无法获得其他任何信息。图6和图7分别给出了传统分布式多方参与计算模型和MPC下的多方参与计算模型。
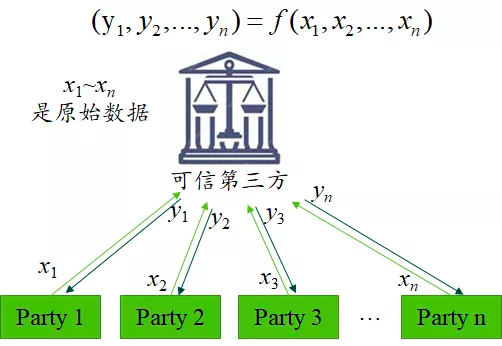
图6 传统分布式多方参与计算模型
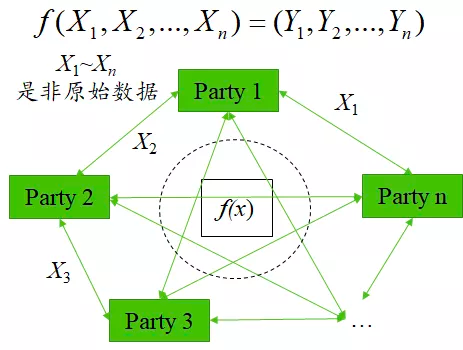
图7 MPC下的多方参与计算模型
在传统分布式计算模型下，传统的分布式计算由中心节点协调各用户的计算进程，收集各参与方的明文输入信息，各参与方的原始数据对第三方来说毫无秘密可言，很容易造成数据泄露。
在MPC计算模式下，不需要可信第三方收集所有参与节点的原始明文数据，只需要各参与节点之间相互交换数据即可，而且交换的是处理后（如同态加密、秘密共享等处理方法）的数据，保证其他参与节点拿到数据后，也无法反推原始明文数据，确保了各参与方数据的私密性。
安全多方计算技术体系架构
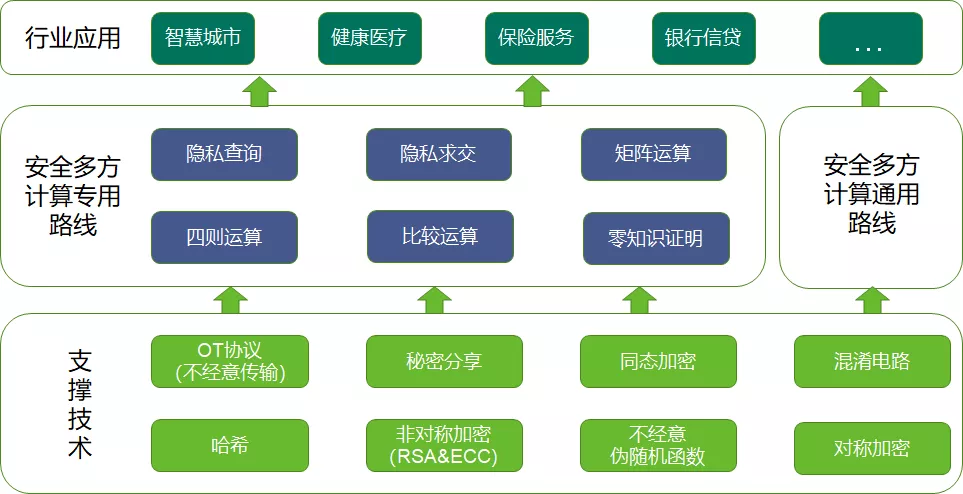
安全多方计算技术体系架构如图所示，多方安全计算技术体系中，最重要的支撑技术有混淆电路(Garbled Circuit)、不经意传输(Oblivious Transfer)、秘密分享(Secret Sharing)、同态加密（HomomorphicEncryption）这四类。本篇文章做为安全多方计算技术的简介篇，暂不对以上每种技术做详细解释，后续系列文章会对以上技术的技术细节以及应用场景逐个进行详细讲解。
图8 安全多方计算技术体系架构
根据支持的计算任务MPC可分为专用场景和通用场景两类。
通用型MPC
通用路线MPC算法一般由混淆电路（GC）实现，具有完备性，理论上可支持任何计算任务。具体做法是将计算逻辑编译成电路，然后混淆执行。
- 优点：理论上可支持任何计算任务
- 缺点：对于复杂计算逻辑，混淆电路的效率会有不同程度的降低
专用型MPC
专用型MPC是指为解决特定问题所构造出的特殊MPC协议，由于是针对性构造并进行优化，专用算法的效率会比基于混淆电路的通用框架高很多，当前MPC专用算法包含四则运算，比较运算，矩阵运算，隐私集合求交集，隐私数据查询等。
- 优点：效率更高
- 缺点：只能支持单一计算逻辑，场景无法通用；专用算法设计需要领域专家针对特定问题精心设计，设计成本高
安全多方计算特点及优势
安全多方计算技术在需要秘密共享和隐私保护的场景中具有重要意义，能解决比较底层的精确计算和数据库查询，其主要适用的场景包括联合数据分析、数据安全查询、数据可信交换等。
安全多方计算具有如下特点及优势：
（1）去中心化。各参与方的地位平等，不存在拥有特权的第三方的参与。
（2）输入数据安全。安全多方计算过程中各方数据输入独立，计算时不泄露任何本地原始数据。
（3）计算结果准确。安全多方计算算法得到结果和原始明文数据本地计算结果保持一致。
总结
安全多方计算拓展了传统分布式计算以及信息安全范畴，为网络协作计算（分布式计算）提供了一种新的计算模式，对解决网络环境下的信息安全具有重要价值[4]。利用安全多方计算协议，一方面可以充分实现数据持有节点间互联合作，另一方面又可以保证秘密的安全性。
对于安全多方计算，在某些特定专用场景下也具有较好性能，如隐私集合求交。然而通用的场景仍然存在诸多是挑战，例如扩展性问题、效率问题以及诚实性问题（输入方可能输入虚假数据或篡改状态数据），这些问题亟需未来进一步研究与解决。
本篇仅简单介绍了安全多方计算技术的起源和技术体系概况，帮助大家了解安全多方计算在数据安全共享场景中的地位以及可以解决的问题。后续文章将详细为大家讲解安全多方计算中的各项基础协议以及应用场景。下篇文章将会为大家讲解不经意传输协议，该协议也是构造基于混淆电路的通用MPC框架的基础协议，敬请期待。
参考文献
[1]Yao A C. Protocols for secure computations[C]// Proc. of the 23rd Annual IEEESymposium on Foundations of Computer Science, 1982.
[2]https://zhiqiang.org/cs/yao-millionaires-problem.html
[3]绿盟科技.《拥抱合规、超越合规：数据安全前沿技术研究报告》[R]. https://www.nsfocus.com.cn/html/2020/92_1229/144.html
[4]https://blog.csdn.net/yuxinqingge/article/details/104588197
