可证明安全
基础
信息安全基本要素
-
机密性
-
完整性
-
可用性
-
可控性
-
可审查性
-
可鉴别性
-
不可抵赖性
-
可靠性
-
公平性
-
隐私性
-
合规性
-
时效性
-
等
信息安全等级保护中，使用机密性、完整性和可用性，简称CIA；
密码学基本属性
-
机密性：信息不被泄漏
-
真实性：信息来源可靠
-
完整性：信息没有被破坏
-
不可否认性：行为不可抵赖
攻击方式
信息安全面临众多威胁，大致可以分为人为威胁和自然威胁。
-
自然威胁，来自天灾，具有无目的性
-
人为威胁，即对信息的人为攻击，通过寻找系统的弱点，以便达到破坏、欺骗、窃取数据等目的。人为攻击分为被动攻击和主动攻击
- 被动攻击，即窃听，如搭线窃听，对文件内容非法复制等，对系统的保密性攻击。主要分为两类：获取消息内容和对业务流分析。因为不对消息作做任何修改，所以被动攻击是难以检测的，对抗方式是预防。
- 主动攻击，是对数据流的某些篡改或产生某些假数据流。可以分为：中断（对系统的可用性攻击）、篡改（对系统的完整性攻击）、伪造（对系统的真实性攻击），对抗方式是检测。
安全防护
-
保密：对应机密性，加密实现
-
认证：对应认证性，签名实现
-
完整性：对应完整性，哈希实现
-
不可否认性：对应不可否认性，签名实现
-
访问控制：认证身份、权限等。
计算复杂度
参考：https://www.cnblogs.com/pam-sh/p/16382557.html#复杂度
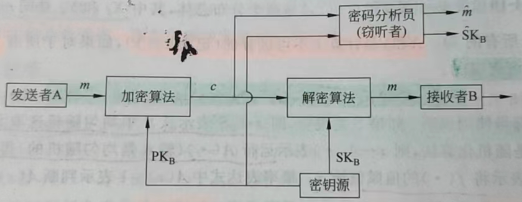
公钥密码体制
相比于单密钥密码体制，公钥密码体制解决了密钥分配和数字签名问题。
加密方案的安全性：拥有公钥的攻击者无法从密文中获取任何明文和私钥信息。
攻击行为
加密算法设计中，安全性受到广泛关注，而可证明安全性理论作为其相关研究领域，是构造密码方案的基本理论，也是目前公钥密码学研究领域的热点。可证明安全性理论的核心是将加密方案的安全性规约到某个算法的困难性上，利用该算法的困难性求解特定的实例问题，该方法被称为加密方案的安全规约证明。
在可证明安全理论中，语义安全一般可由不可区分性游戏（IND游戏）来给出。
游戏模型主要包括敌手和挑战者，挑战者建立加密方案，敌手对该加密方案进行攻击，同时挑战者应对敌手的攻击。
在可证明安全过程中，通常根据游戏模型中攻击者的攻击能力不同，将不可区分性游戏分为:
- 选择明文攻击的不可区分性（Indistinguishability Chosen Plaintext Attack,IND-CPA）
- 选择密文攻击的不可区分性（Indistinguishability Chosen Ciphertext Attack,IND-CCA）
- 适应性选择密文攻击的不可区分性（Adaptive Chosen Ciphertext Attack, IND-CCA2）
常用的攻击方法可分为以下三类：
选择明文攻击
选择明文攻击(Chosen Plaintext Atack, CPA)。在选择明文攻击中，除目标明文外，敌手可产生明文密文对，并利用得到的明文密文对完成对加密方案的攻击【想获取目标明文和密钥】。具体来说，敌手产生任意明文【除目标明文外】，可访问一个加密黑盒（加密预言机），得到对应密文，但不能执行解密。在密码方案实际使用的过程中，CPA模拟了一种较弱的攻击行为。
公钥加密方案在选择明文攻击CPA下的IND游戏如下：
- 初始化：挑战者产生系统$\Pi $，敌手（A）获得系统的公开钥
- （训练）：敌手产生除目标明文的任意明文消息，通过【加密预言机】得到系统加密后的密文（多项式时间内）
- 挑战：敌手输出两个长度相同的明文消息\(M_0\)和\(M_1\)。挑战者随机选择$\beta \in \left {0,1 \right } \(，将\)M_{\left {0,1 \right } }\(加密，并将密文\)C^*$（目标密文）给敌手。
- 猜测：敌手输出\(\beta ^‘\)，如果\(\beta ^‘=\beta\)，则敌手攻击成功。
敌手优势函数定义为：\(Adv_{\pi, A}^{\operatorname{CPA}}(\mathcal{K})=\left|\operatorname{Pr}\left[\beta^{\prime}=\beta\right]-\frac{1}{2}\right|\)，其中\(K\)是安全参数，用于确定加密方案的密钥长度，若优势函数\(Adv_{\pi, A}^{\operatorname{CPA}}\)是可忽略的，则该公钥加密方案是IND-CPA安全的。
第二步的“训练”，可以看作是敌手发起挑战钱对自己的训练（自学），可以通过挑战着，也可以通过加密预言机。
选择密文攻击
选择密文攻击(Chosen Cipertext Accack, CCA1)。选择密文攻击也被称为午餐攻击，敌手可访问一个解密黑盒。即午餐时间（规定时间内）敌手可选择除目标密文外的特定密文，询问并通过访问解密预言机进行解密，访问解密预言机要在午餐时间完成。因为能够访问解密预言机，CCA1使得敌手拥有比CPA攻击更强的能力。
午餐时间：可以理解为，掌握黑盒的人有一个解密运算的黑盒，他在午餐时间离开后，敌手能够使用该黑盒对自己所选择的密文解密，等午餐时间过后，敌手就不能再使用了。
公钥加密方案在选择密文攻击CCA下的IND游戏如下：
- 初始化：挑战者产生系统$\Pi $，敌手（A）获得系统的公开钥
- （训练）：敌手向挑战者（或解密预言机）做解密询问（多项式时间内），即发密文给挑战者（预言机），解密后返回给敌手
- 挑战：敌手输出两个长度相同的明文消息\(M_0\)和\(M_1\)。再从挑战者接收\(M_{\beta }\)的密文，其中随机选择$\beta \in \left {0,1 \right } $。
- 猜测：敌手输出\(\beta ^‘\)，如果\(\beta ^‘=\beta\)，则敌手攻击成功。
敌手优势函数定义为：\(Adv_{\pi, A}^{\operatorname{CCA}}(\mathcal{K})=\left|\operatorname{Pr}\left[\beta^{\prime}=\beta\right]-\frac{1}{2}\right|\)，其中\(K\)是安全参数，用于确定加密方案的密钥长度，若优势函数\(Adv_{\pi, A}^{\operatorname{CCA}}\)是可忽略的，则该公钥加密方案是IND-CCA安全的。
自适应选择密文攻击
自适应选择密文攻击(Adaptive Chosen Cipertext Accack,CCA2)。自适应性选择密文攻击除目标密文外，敌手可选择任何密文对解密盒进行询问（多次），目前一般要求公钥加密算法要在自适应选择密文攻击达到多项式安全。CCA2攻击行为下的敌手的攻击能力与CCA1相比更强大。
公钥加密方案在选择密文攻击CCA2下的IND游戏如下：
- 初始化：挑战者产生系统$\Pi $，敌手（A）获得系统的公开钥
- （训练1）：敌手向挑战者（或解密预言机）做解密询问（多项式时间内），即发密文给挑战者（预言机），解密后明文返回给敌手
- 挑战：敌手输出两个长度相同的明文消息\(M_0\)和\(M_1\)。再从挑战者接收\(M_{\beta }\)的密文，其中随机选择$\beta \in \left {0,1 \right } $
- （训练2）：敌手向挑战者（或解密预言机）做解密询问（多项式时间内），即发密文给挑战者（预言机），解密后返回明文给敌手
- 猜测：敌手输出\(\beta ^‘\)，如果\(\beta ^‘=\beta\)，则敌手攻击成功。
敌手优势函数定义为：\(Adv_{\pi, A}^{\operatorname{CCA2}}(\mathcal{K})=\left|\operatorname{Pr}\left[\beta^{\prime}=\beta\right]-\frac{1}{2}\right|\)，其中\(K\)是安全参数，用于确定加密方案的密钥长度，若优势函数\(Adv_{\pi, A}^{\operatorname{CCA2}}\)是可忽略的，则该公钥加密方案是IND-CCA2安全的。
安全目标
安全目标分为两类：
不可区分性（IND）
给定一个挑战密文，敌手无法获取对应明文的任何信息泄露。对于基于比特的明文加密方案，敌手在得到挑战密文的条件下，也无法正确得到对应的比特明文，也就是说敌手攻击成功的概率为1/2。
以IND-CPA为例：
非延展性（NM）
一个可延展的加密体制在适应性选择密文攻击CCA2下是不安全的。因此要求方案具有非延展性，非延展性指的是给定一个挑战密文c ，对应的明文为$\mu $，敌手无法获取到另外一个密文c'，该密文对应的明文为 \(\mu '\)，且两个明文$\mu $ 和 \(\mu '\)是相互独立的。
依据攻击行为和安全目标的区别，可分别得到IND-CPA，IND-CCA1，INDCCA2，NM-CPA，NM-CCA1，NM-CCA2等多个安全模型。
我们称加密方案是安全的，如果加密方案在某种安全模型下是可证安全的，一般情况下可证明IND-CPA安全和语义安全是等价的。
下面对可证明安全涉及到的几个重要定义进行介绍：
优势函数
计算不可区分
参考
- 现代密码学-杨波
- 信息安全工程师5天修炼-施游
- 密码学中的可证明安全性-杨波
- “完全或无”、IND-CPA、IND-CCA1、IND-CCA2的详细说明
- 密码攻击
