ElGamal算法
ElGamal原论文:A public key cryptosystem and a signature scheme based on discrete logarithms-1985
论文
摘要

基于有限域上的离散对数问题提出一种新的签名方案和一种新的公钥加密方案。
介绍

1976年,DH两人介绍了一种公钥加密算法【New directions in cryptography】,后面很多人给出了一些公钥加密方案,比如RSA公钥加密方案,基于大整数难分解问题。本文主要基于有限域上的离散对数问题。
- 第一介绍了一种公钥加密方案
- 第二介绍一种签名方案
- 第三个给出针对签名方案的一些攻击分析
- 第四给出该系统的一些性质
- 第五总结和一些补充
公钥加密方案

首先介绍DH密钥协商协议:
(1)参与方\(A\)和\(B\)想要共享一个密钥\(K_{AB}\),其中\(A\)有密钥\(x_A\),\(B\)有密钥\(x_B\)。其中\(p\)是一个大素数,\(\alpha\)是模\(p\)的本原(primitive element),公开的。
(2)\(A\)计算\(y_A=\alpha ^{x_A}mod p\),发送给\(B\)
(3)同样,\(B\)计算\(y_B=\alpha ^{x_B}mod p\),发送给\(A\)
(4)这样协商的密钥\(K_{AB}\)就计算出来了
任何基于离散对数问题的密码算法,\(p\)的选择是很重要的,必须保证\(p-1\)是一个大素数因子,如果\(p\)是一个小素数的话,那么求解离散对数问题就变的简单了。
下面看一下\(A\)想要给\(B\)发送一条消息\(m\in [0,p-1]\)的过程:
(1)\(A\)选取一个数\(k\in [0,p-1]\),这里的\(x_A=k\);计算\(K=y_B^k mod p\),其中\(y_B=\alpha ^{x_B}mod p\)要么是公开的,要么是\(B\)发过来的。
这里不建议使用相同的\(k\)加密多个消息,因为可能会泄露出明文消息,例如:
这样就有\(m_1/m_2=c_1/c_2mod p\),已知\(m_2\),就能求出\(m_1\)
(2)\(A\)加密消息\(m\)为\((c_1=\alpha ^k mod p,c_2=K*m mod p)\)。
这里提到,乘法运算是可以被任何可逆运算替换的,比如模加(addition mod p)
(3)解密运算分为两步:第一步恢复\(K\),对于\(B\)来说,\(x_B\)是已知的,可以计算出\(K=(\alpha ^k)^{x_B}=(c_1)^{x_B}\);第二步是\(c_2/K\),恢复出\(m\)
下面说明方案的安全性:破解该方案就相当于破解DH密钥协商协议。
- 第一,\(B\)能在不知道\(k\)的情况下,计算出\(K\);
- 第二,\(B\)已知\(K\)和\(y_B\),也不能计算出\(k\)(基于离散对数问题)
签名方案
下面以\(m\in [0,p-1]\)为被签名的文件,公钥\((y=\alpha ^x mod p,\alpha,p)\) ,用于\(A\)使用私钥\(x_A\)签名了文件\(m\),其它用户就可以使用自己的公钥\(y_A\)去验签。
\(m\)的签名是\((r,s)\in [0.p-1]\),且满足\(\alpha ^m=y^r*r^s mod p\)
签名

最后得到满足条件的签名\((r,s)\)
和加密一样,这里的随机数\(k\)不能重复使用,每次签名都需要重新选取。
验签
给出\((r,s)\)和\(m\),通过验证(3)公式两边是否相等验证。
攻击
将方案的安全性规约到离散对数问题上,攻击可以分为两种:
(1)恢复密钥\(x\)
(2)伪造签名
性能对比
加密方案
(1)加密引入随机数,加密相同密文,得到的密文是不同的,防止重访攻击,其中RSA不具备该性质
(2)加密时,需要两次幂运算,相当于\(GF(p)\)上进行\(2logp\)乘法;解密时只需一次幂运算(和一次除法(求逆))
签名方案
(1)签名时,需要一次幂运算(加一些乘法运算);验签时,需要三次幂运算
总结
介绍了基于有限域\(GF(p)\)上离散对数问题的公钥加密方案和签名方案。对于公钥加密方案可以扩展到\(GF(p^m)\)上(这会使得方案的密钥很大),其中\(m=3,4\)效果会更好。与RSA相比,公钥和密文的大小使其的2倍。
公钥加密方案
和上述论文中的公钥加密方案对应
乘法同态

RSA与ElGamal的区别

签名算法

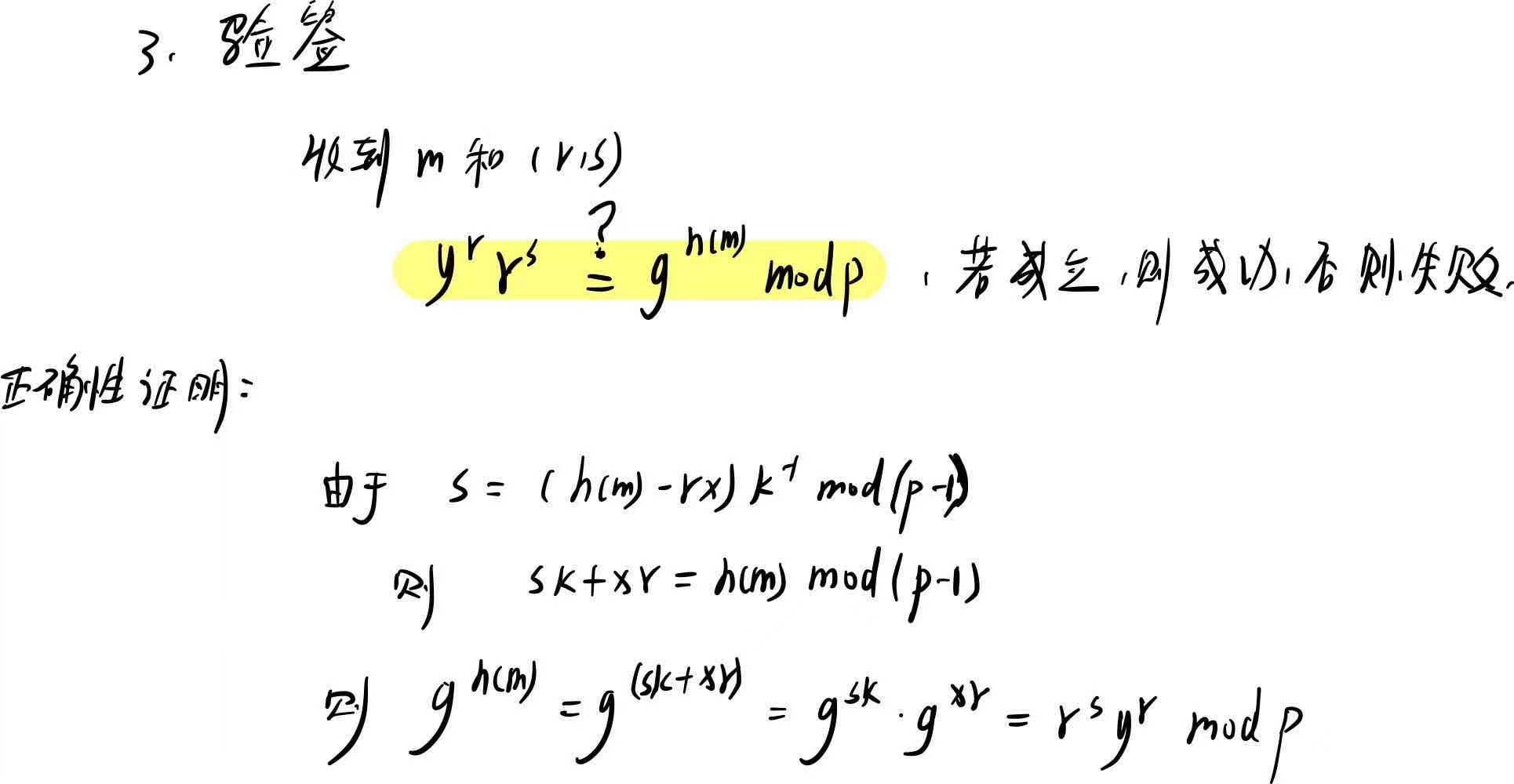
参考
1、密码基础
2、基于ElGamal的同态交换加密水印算法_方立娇

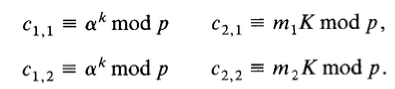

 浙公网安备 33010602011771号
浙公网安备 33010602011771号