AES 逻辑
分组长度


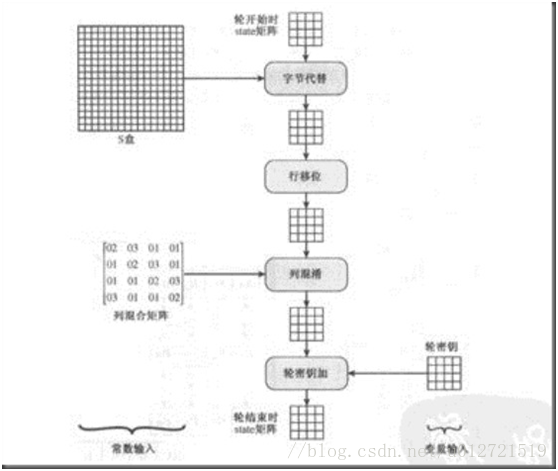
加密逻辑
轮函数
参考:链接
字节代换
两种方法:
1、首先(将字节看做GF(28)上的元素,映射到自己的乘法逆元)换成人话就是(对多项式的逆,参考:链接);
其次,对字节做仿射变换

2、直接查表,找出S盒中对应的值即可
映射方式:
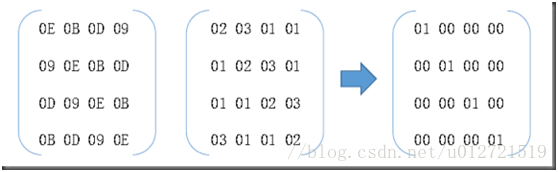
把该字节的高4位作为行值,低4位作为列值,以这些行列值作为索引从S盒中对应位置取出元素作为输出。例如,十六进制数{95}所对应的S盒的行值是9,列值是5,S盒中在此位置的值是{2A},相应的{95}被映射为{2A}。
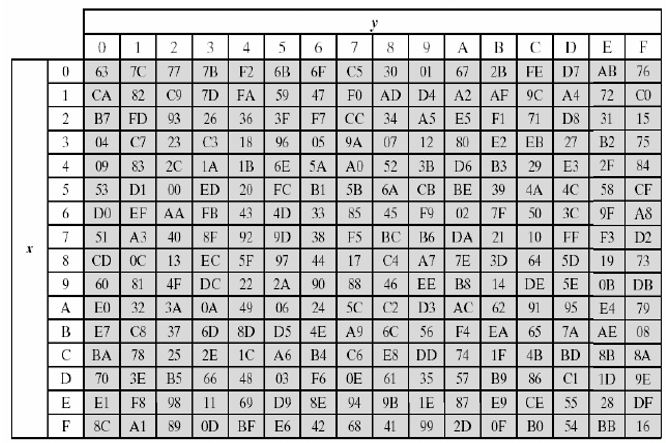
逆代换S盒:
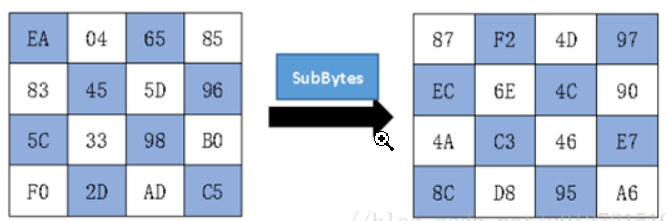
下面是一个字节代替的例子:
行移位
正向和逆向变换。正向行移位,state的第一行保持不变。把state的第二行循环左移一个字节,state的第三行循环左移两个字节,state的第四行循环左移三个字节。
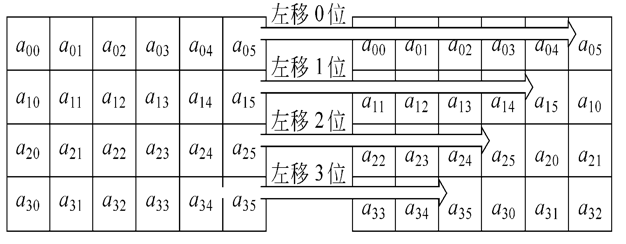
逆向行移位将state中的后三行执行相反方向的移位操作,如第二行向右循环移位一个字节,其他类似操作。
列混合
正向和逆向变换。
列混淆变换的正向列混淆变换对每列独立地进行操作。每列中的每个字节被映射为一个新值,此值由该列中的4个字节通过函数变换得到。
列混淆例子:

计算过程:
47 = (02•87)⊕(03•6E)⊕(01•4A)⊕(01•A6)
其中:
02•87 = 02•10000111B = 00001110B⊕00011011B =00010101B = 15
03•6E = (01⊕02)•6E = (01•6E)⊕(02•6E)
= 01101110B⊕(11011100B)= 10110010B = B2
01•46 = 46
01•A6 = A6
15⊕B2⊕46⊕A6 = 47
注意: G(28)上的运算
加法:按位异或
乘法:可通过对多个中间结果的移位运算和异或一个特定的比特串(比如00011011)实现。(与最高位b7有关)
逆向列混淆变换可以再乘以矩阵的逆得到
再例如:

轮秘钥相加
秘钥加就是将子秘钥简单地与状态进行逐比特异或。

逆向轮密钥加变换是和正向轮密钥加变换一样的,因为异或操作是其本身的逆。
A⊕B⊕B = A
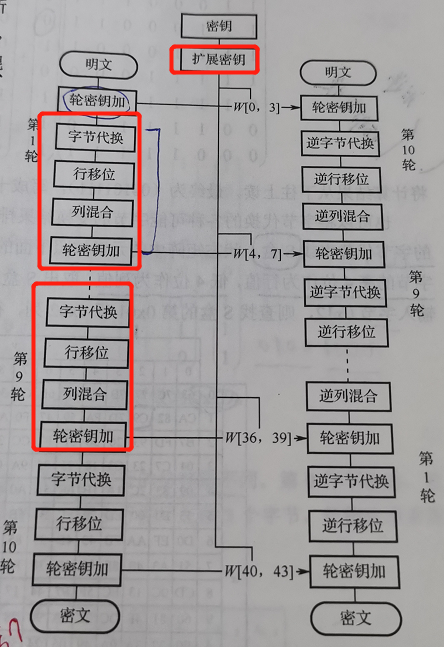
单轮AES输入:
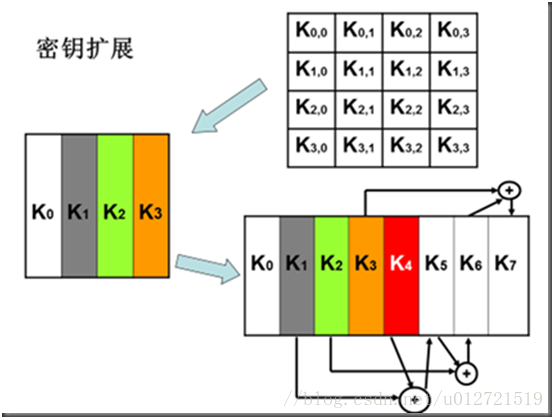
秘钥扩展
从一个原始秘钥中生成多重秘钥以代替使用单个秘钥,大大增加了比特位的扩散。
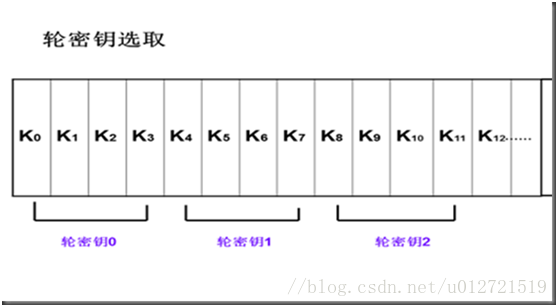
输入四字秘钥,输出一个44字的一维线性数组,前四个元素为原始秘钥,用于加密运算中的初始秘钥加,后40个字分为10组,每组4个字(128位)分别用于10轮运算中的轮秘钥加。
原理
1、AES首先将初始密钥按照列优先的顺序,输入到一个4*4矩阵中:

这个4*4矩阵的每一列的4个字节组成一个字,矩阵4列的4个字一次命名为w[0],w[1],w[2],w[3]。它们构成了一个以字为单位的数组w。
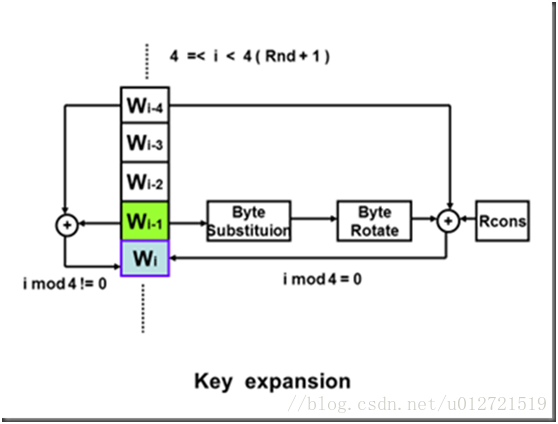
接着,对数组w扩充40个新列,构成总共44列的扩展密钥数组。新列按照一下的递归方式产生:
(1)如果 i 不是4的倍数,那么第 i 列由如下等式确定:w[i]=w[i-4] ⨁w[i-1];
(2)如果 i 是4的倍数,那么第 i 列由如下等式确定:w[i]=w[i-4] ⨁T(w[i-1]),其中,T是一个复杂函数
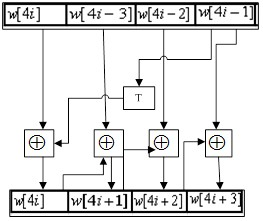
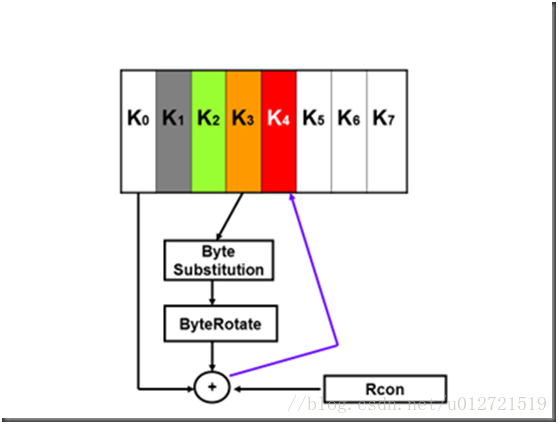
函数T由3部分组成:字循环、字节代换和轮常量异或,这3部分的作用分别如下:
(1)字循环:将1个字中的4个字节循环左移一个字节,即将输入字[b0,b1,b2,b3]变换成[b1,b2,b3,b0]。
(2)字节代换:对字循环的结果使用AES的S盒进行字节代换。
(3)轮常量异或:将前两步的结果同轮常量 Rcon[j] 进行异或,其中j表示轮数。

2、用图表示:
AES-GCM加密算法
转载:链接
GCM ( Galois/Counter Mode) 指的是该对称加密采用Counter模式,并带有GMAC消息认证码
ECB( Electronic Mode 电子密码本模式)
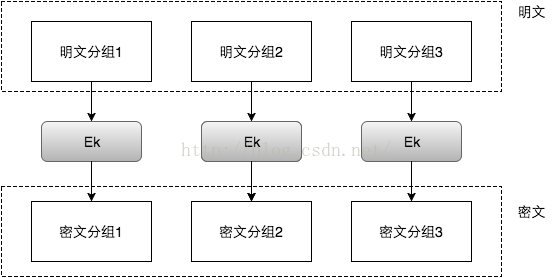
当我们有一段明文,需要对其进行AES加密时,需要对明文进行分组,分组长度可为128,256,或512bits。采用ECB模式的分组密码算法加密过程如下图:
由上图可以看出,明文中重复的排列会反映在密文中。
并且,当密文被篡改时,解密后对应的明文分组也会出错,且解密者察觉不到密文被篡改了。也就是说,ECB不能提供对密文的完整性校验。
因此,在任何情况下都不推荐使用ECB模式。
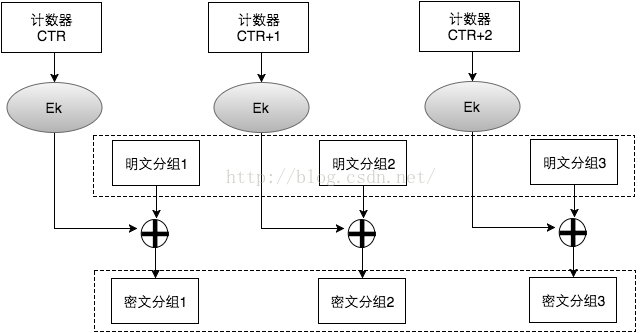
CTR ( CounTeR 计数器模式)
在计数器模式下,我们不再对密文进行加密,而是对一个逐次累加的计数器进行加密,用加密后的比特序列与明文分组进行 XOR得到密文。过程如下图:
计数器模式下,每次与明文分组进行XOR的比特序列是不同的,因此,计数器模式解决了ECB模式中,相同的明文会得到相同的密文的问题。CBC,CFB,OFB模式都能解决这个问题,但CTR的另两个优点是:1)支持加解密并行计算,可事先进行加解密准备;2)错误密文中的对应比特只会影响明文中的对应比特等优点。
但CTR仍然不能提供密文消息完整性校验的功能。
有的人可能会想到,如果将密文的hash值随密文一起发送,密文接收者对收到的密文计算hash值,与收到的hash值进行比对,这样是否就能校验消息的完整性呢?
再仔细想想,就能发现这其中的漏洞。当篡改者截获原始的密文消息时,先篡改密文,而后计算篡改后的密文hash, 替换掉原始消息中的密文hash。这样,消息接收者仍然没有办法发现对源密文的篡改。可见,使用单向散列函数计算hash值仍然不能解决消息完整性校验的问题。
MAC ( Message Authentication Code, 消息验证码)
想要校验消息的完整性,必须引入另一个概念:消息验证码。消息验证码是一种与秘钥相关的单项散列函数。
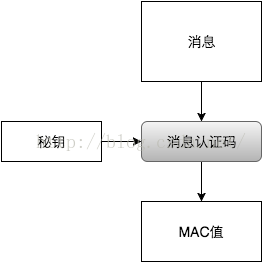
密文的收发双发需要提前共享一个秘钥。密文发送者将密文的MAC值随密文一起发送,密文接收者通过共享秘钥计算收到密文的MAC值,这样就可以对收到的密文做完整性校验。当篡改者篡改密文后,没有共享秘钥,就无法计算出篡改后的密文的MAC值。
如果生成密文的加密模式是CTR,或者是其他有初始IV的加密模式,别忘了将初始的计时器或初始向量的值作为附加消息与密文一起计算MAC。
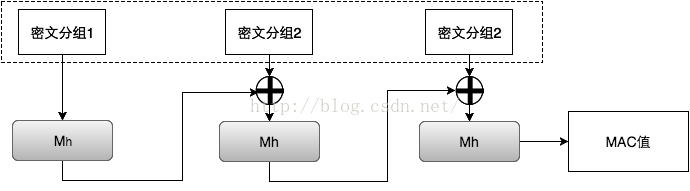
GMAC ( Galois message authentication code mode, 伽罗瓦消息验证码 )
对应到上图中的消息认证码,GMAC就是利用伽罗华域(Galois Field,GF,有限域)乘法运算来计算消息的MAC值。假设秘钥长度为128bits, 当密文大于128bits时,需要将密文按128bits进行分组。应用流程如下图:
GCM( Galois/Counter Mode )
GCM中的G就是指GMAC,C就是指CTR。
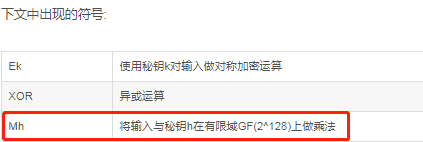
GCM可以提供对消息的加密和完整性校验,另外,它还可以提供附加消息的完整性校验。在实际应用场景中,有些信息是我们不需要保密,但信息的接收者需要确认它的真实性的,例如源IP,源端口,目的IP,IV,等等。因此,我们可以将这一部分作为附加消息加入到MAC值的计算当中。下图的Ek表示用对称秘钥k对输入做AES运算。最后,密文接收者会收到密文、IV(计数器CTR的初始值)、MAC值。